As shown below AB represents an infinite wall tangential to a horizontal semi-circular track. O is a point source of light on the ground at the centre of the circle. A block moves along the circular track with a speed v starting from the point where the wall touches the circle. If the velocity and acceleration of shadow along the length of the wall is respectively V and a, then :

V=vcos(vtR)
V=vsec2(vtR)
a=(v2R)sec2(vtR)tan(vtR)
a=(2v2R)sec2(vtR)tan(vtR)
The correct Answer is:b,d
Topper's Solved these Questions
- FORCE ANALYSISBook:ANURAG MISHRAChapter:FORCE ANALYSISExercise:Level-3
Explore 49 Videos
- FORCE ANALYSISBook:ANURAG MISHRAChapter:FORCE ANALYSISExercise:Matching type
Explore 13 Videos
- FORCE ANALYSISBook:ANURAG MISHRAChapter:FORCE ANALYSISExercise:level 1
Explore 103 Videos
- DESCRIPTION OF MOTIONBook:ANURAG MISHRAChapter:DESCRIPTION OF MOTIONExercise:Level-3
Explore 34 Videos
- IMPULSE AND MOMENTUMBook:ANURAG MISHRAChapter:IMPULSE AND MOMENTUMExercise:matching
Explore 3 Videos
Similar Questions
A man running along a circular track has the speedof 10 km per hour. A source of light is at the centre of the circular track. A wall is along the tangent to the circular track at the point from which he starts.What is the speed of the shadow of the man on the wall when he covers 18th of the track? (Assume thetrack to be a line.)
View SolutionOn a particle moving on a circular path with constant speed v, light is thrown from a projectors placed at the centre of the circular path. The shadow of the particle is formed on the wall. The velocity of shadow up the wall is
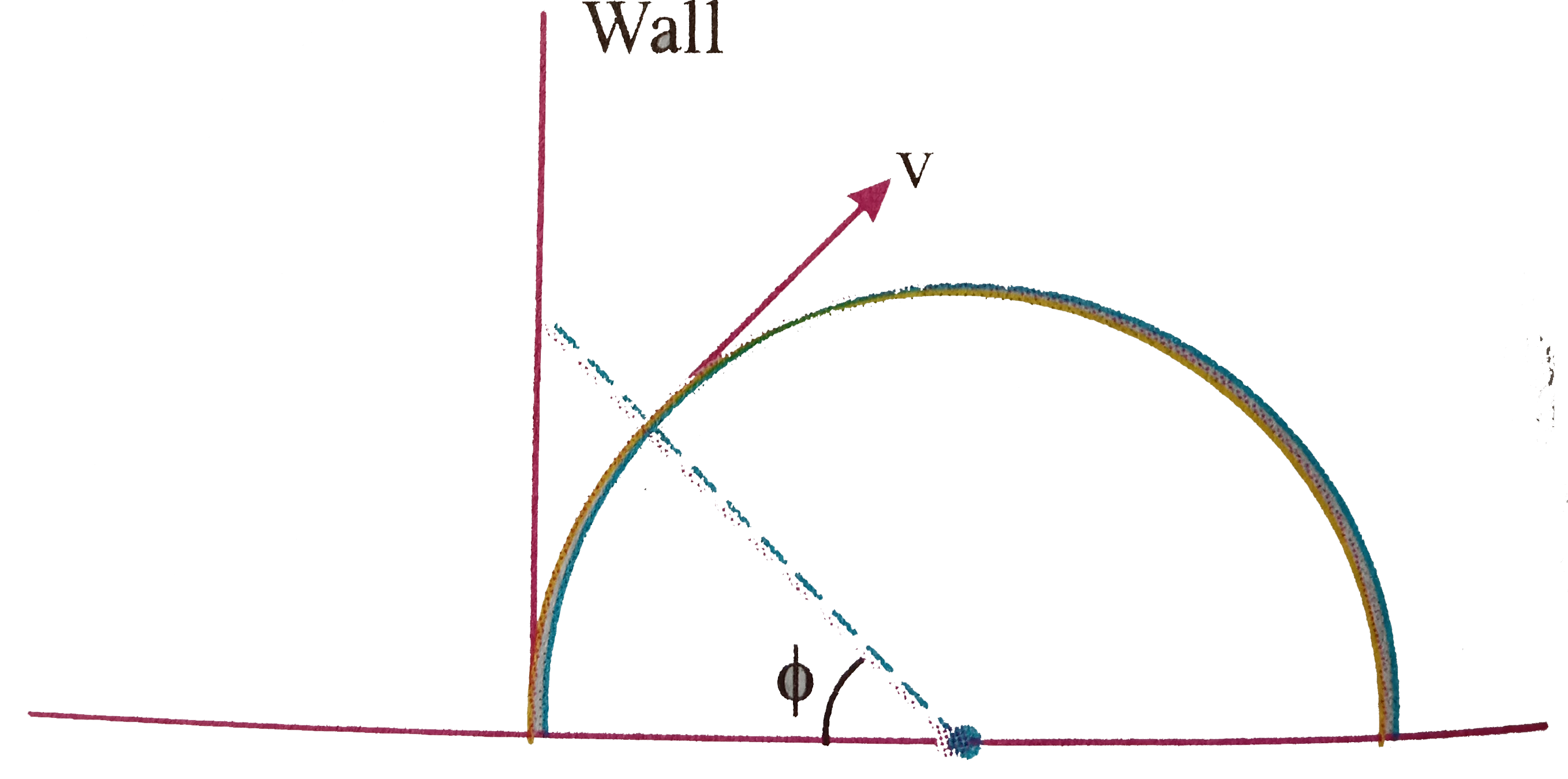
View Solution
Knowledge Check
As shown in figure AB represents an infinite wall tangential to a horizontal semi circular track.O is a point source of light on the ground at the centre of the circle. A block moves along the circular track with speed v starting from the point where the wall touches the circle. If the velocity and acceleration of shadow along the length of the wall is respectively 'V' and 'a' then,
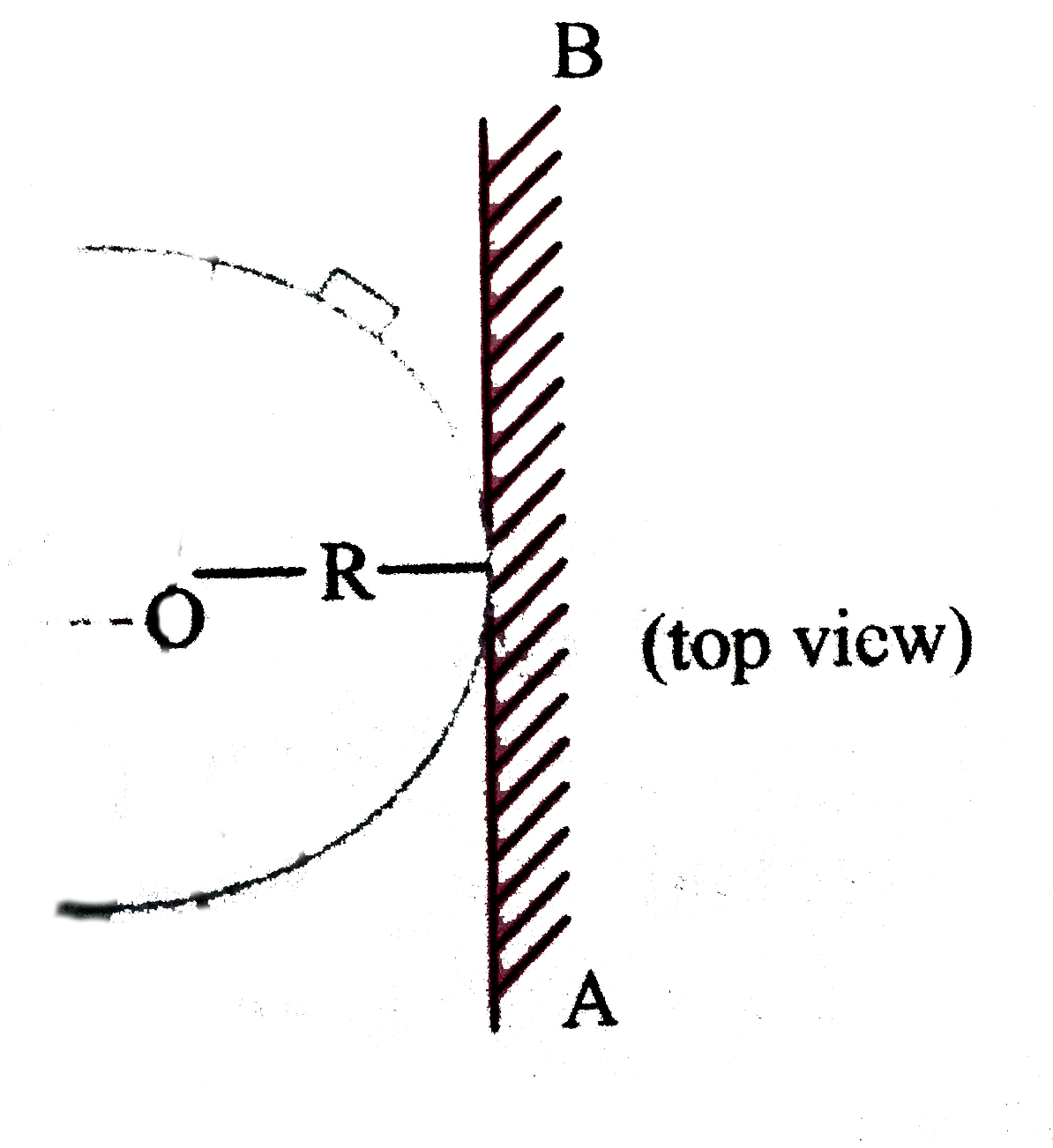 AV=vcosvtRBV=vsec2(vtR)Ca=v2Rsec2(vtR)tan(vtR)Da=2v2Rsec2(vtR)tan(vtR)
AV=vcosvtRBV=vsec2(vtR)Ca=v2Rsec2(vtR)tan(vtR)Da=2v2Rsec2(vtR)tan(vtR)On a particle moving on a circular path with constant speed v, light is thrown from a projectors placed at the centre of the circular path. The shadow of the particle is formed on the wall. The velocity of shadow up the wall is
 Avsec2φBvcos2φCvcosφDNone of these
Avsec2φBvcos2φCvcosφDNone of theseA particle moves with constant speed v along a circular path of radius r and completes the circle in time T. The acceleration of the particle is
A2πv/TB2πr/TC2πr2/TD2πv2/T
A particle moves with constant speed v along a circular path of radius r and completes the circle in time T. The acceleration of the particle is
View SolutionA point moves along a circle with a velocity v=t/2. Find the acceleration of the point at the moment when it has covered a quarter circle from the beginning of motion.
View SolutionBlock A is moving away from the wall at a speed v and acceleration a.

View SolutionA block of mass m is placed on a circular track and then it is given a velocity υ vertically downwards at position A on track. If block moves on track with constant speed, then

View SolutionBlock A is moving away from the wall at a speed v and acceleration a.

View Solution

