A particle of mass m moves along a circle of 'R'. The modulus of the average vector of force acting on the particle over the distance equal to a quarter of the circle is :
zero if the particle moves with uniform speed v
√2mv2πR if the particle moves with uniform speed v
√2mv2πR if the particle moves with uniform speed v
ma if particle moves with constant tangential acceleration 'a', the initial velocity being equal to zero
The correct Answer is:c
Step by step video, text & image solution for A particle of mass m moves along a circle of 'R'. The modulus of the average vector of force acting on the particle over the distance equal to a quarter of the circle is : by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- FORCE ANALYSISBook:ANURAG MISHRAChapter:FORCE ANALYSISExercise:Level-3
Explore 49 Videos
- FORCE ANALYSISBook:ANURAG MISHRAChapter:FORCE ANALYSISExercise:Matching type
Explore 13 Videos
- FORCE ANALYSISBook:ANURAG MISHRAChapter:FORCE ANALYSISExercise:level 1
Explore 103 Videos
- DESCRIPTION OF MOTIONBook:ANURAG MISHRAChapter:DESCRIPTION OF MOTIONExercise:Level-3
Explore 34 Videos
- IMPULSE AND MOMENTUMBook:ANURAG MISHRAChapter:IMPULSE AND MOMENTUMExercise:matching
Explore 3 Videos
Similar Questions
A particle of mass m moves along a circle of radius R. Find the modulus of the average vector of the force acting on the particle over the distance equal to a quarter of the circle, if the particle moves
(a) uniformly with velocity v,
(b) with constant tangential acceleration wτ, the initial velocity being equal to zero.
View SolutionA particles of mass m moving in a circle of radius r with unform speed v. The force F acting on a particle is proportional ot mavbrc. Find the values of a, b and c.
View Solution
Knowledge Check
A particle of mass m is moving along a circle of radius r with a time period T. Its angular momentum is
A2πmrTB4πmrTC2πmr2TD4πmr2TA particle is projected so as to just move along a vertical circle of radius r. The ratio of the tension in the string when the particle is at the lowest and highest point on the circle is -
A1Bfinite but largeCzeroDInfiniteStarting from rest, a particle rotates in a circle of radius R 2 m with an angular acceleration = /4 rad/s2.The magnitude of average velocity of the particle over the time it rotates quarter circle is:
A1.5m/sB2m/sC1m/sD1.25m/s
Two particles each of equal mass (m) move along a circle of radius (r) under the action of their mutual dravitational. Find the speed of each particle.

View SolutionFour particles each of mass M, move along a circle of radius R under the action of their mutual gravitational attraction as shown in figure. The speed of each particle is :
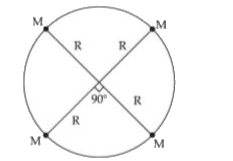
View SolutionThe kinetic energy K of a particle moving along a circle of radius R depends upon the distance s as K=as2. The force acting on the particle is
View SolutionFour particles each of mass M move along a circle of radius R under the action of their mutula gravitational attraction the speed of each paritcles is
View SolutionA particle of mass m is moving is a horizontal circle of radius x under a centripetal force equal to −(kv2) where it is constant The total energy of the particle is
View Solution

