A particle P is attached by means of two equal strings to two points A and B is same vertical line and describes horizontal circle with uniform angular speed where AB = h
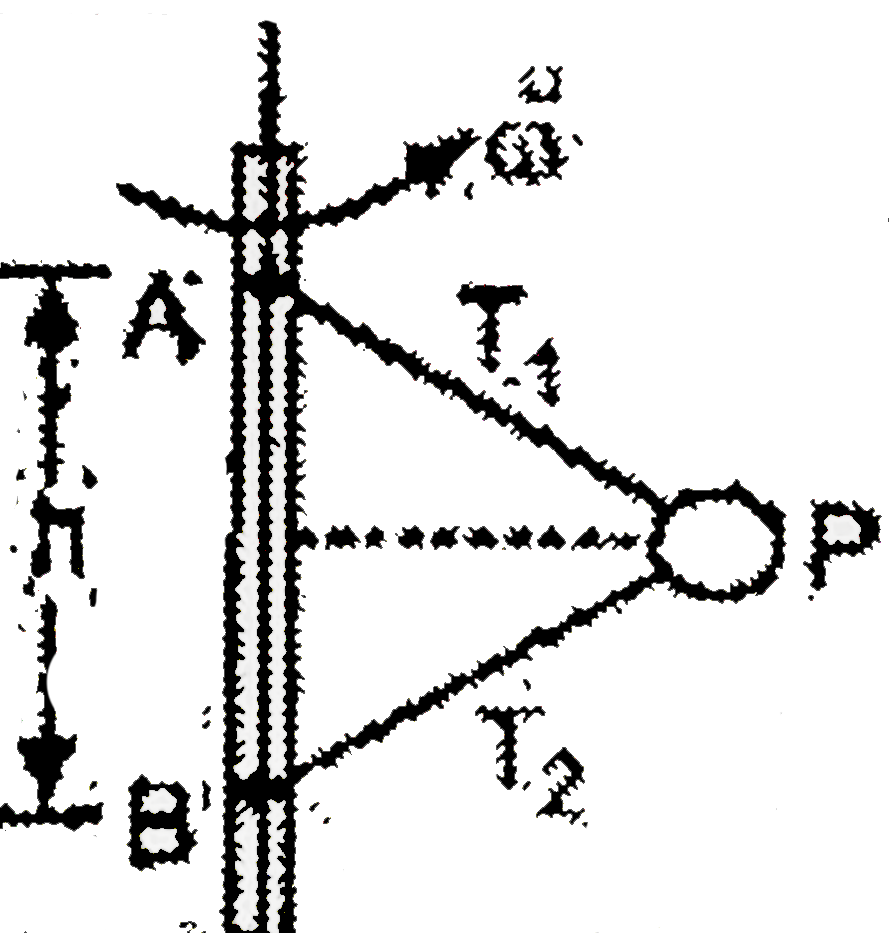
The correct Answer is:a,b
Step by step video, text & image solution for A particle P is attached by means of two equal strings to two points A and B is same vertical line and describes horizontal circle with uniform angular speed 2 sqrt((2g)/(h)) where AB = h by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- FORCE ANALYSISBook:ANURAG MISHRAChapter:FORCE ANALYSISExercise:Level-3
Explore 49 Videos
- FORCE ANALYSISBook:ANURAG MISHRAChapter:FORCE ANALYSISExercise:Matching type
Explore 13 Videos
- FORCE ANALYSISBook:ANURAG MISHRAChapter:FORCE ANALYSISExercise:level 1
Explore 103 Videos
- DESCRIPTION OF MOTIONBook:ANURAG MISHRAChapter:DESCRIPTION OF MOTIONExercise:Level-3
Explore 34 Videos
- IMPULSE AND MOMENTUMBook:ANURAG MISHRAChapter:IMPULSE AND MOMENTUMExercise:matching
Explore 3 Videos
Similar Questions
A particle is attached by means of two equal strings to two points A and B in the same vertical line and describes a horizontal circle with a uniform angular speed. If the angular speed of the particle is 2√2g/h with AB=h, show that the ratio of the tensions of the strings is 5:3
View SolutionA particle of mass 21 g attached to a string of 70cm length Keeping the string always taut the ball describes a horizontal circle of radius 15cm Calculate the angular speed of the ball .
View Solution
Knowledge Check
A particle is attached by a light string of length 3 a to a fixed point and describes a horizontal circle of radius a with uniform angular velocity ω If, when the particle is moving in this manner, is suddenly stopped and then let go,find its velocity when the string is vertical in its subsequent motion :
A[2ga(3−2√2)]1/2B2ga(3−2√2)Cga(3−2√2)D2ga3−2√2A particle of mass m1 is fastened to one end of a string and one of m2 to the middle point, the other end of the string being fastened to a fixed point on a smooth horizontal table The particles are then projected, so that the two portions of the string are always in the same straight line and describes horizontal circles find the ratio of tensions in the two parts of the string
 Am1m1+m2Bm1+m2m1C2m1+m22m1D2m1m1+m2
Am1m1+m2Bm1+m2m1C2m1+m22m1D2m1m1+m2A bob of mass m attached to an inextensible string of length I is suspended from a vertical support. The bob rotates in a horizontal circle with an angular speed ω red/s about the vertical. About the point of suspension:
Aangular momentum is conserved.Bangular momentum changes in magnitude but not is direction.Cangular momentum changes in direction but not in magnitude.Dangular momentum changes both in direction and magnitude.
A heavy particle of mass 2kg is tied to two strings, each of length 25 cm and they are tied to two points 30 cm apart on the same vertical line. The particle is whirled in a horizontal plane with a speed of 1.8ms−1. Calculate the ratio of the tensions of the two strings.
View SolutionA particle of mass m1 is fastened to one end of a massless string and another particle of mass m2 is fastened to the middle point of the same string. The other end of the string being fastened to a fixed point on a smooth horizontal table. The particles are then projected, so that the two particles and the string are always in the same straight line and describe horizontal circles. Then, the ratio of rotations in the two parts of the string is :
View SolutionA particle of mass m is attached to one end of a light inextensible string and the other end of the string is fixed in vertical plane as shown. Particle is given a horizontal velocity u=√52gl
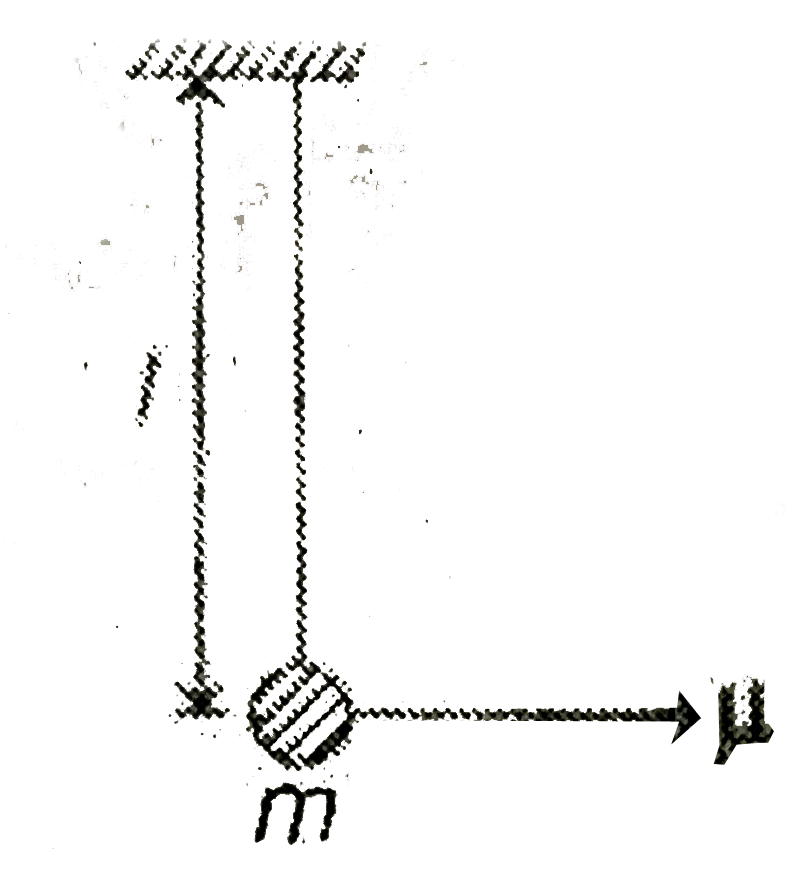
The tension in the string at an instant when acceleration of the particle is horizontal and √3g is
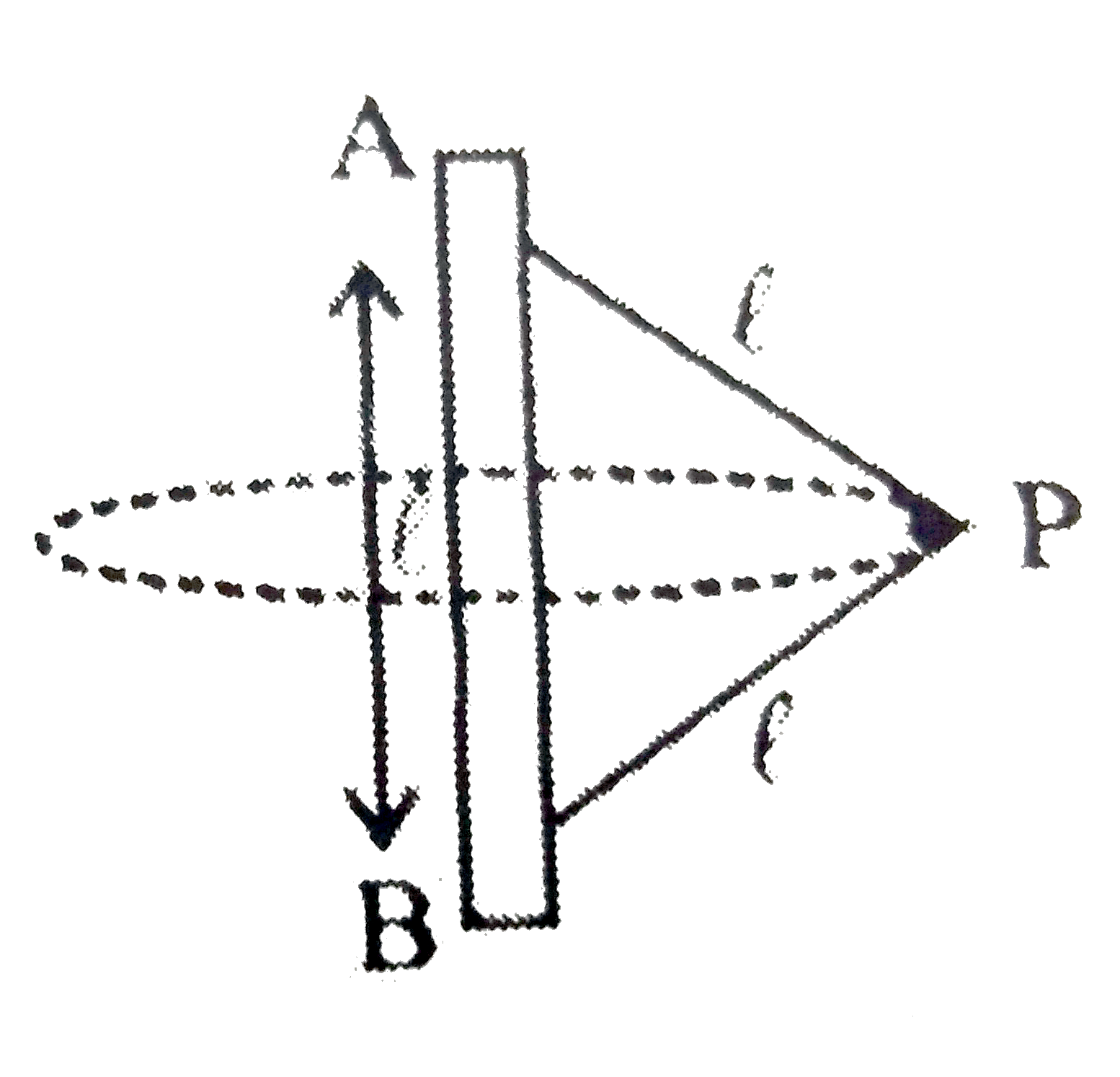
View SolutionA particle P of mass m is attached to a vertical axis by two strings AP and BP of length l each. The separation AB=l. P rotates around the axis with an angular velocity ω. The tensions in the two strings are T1andT2
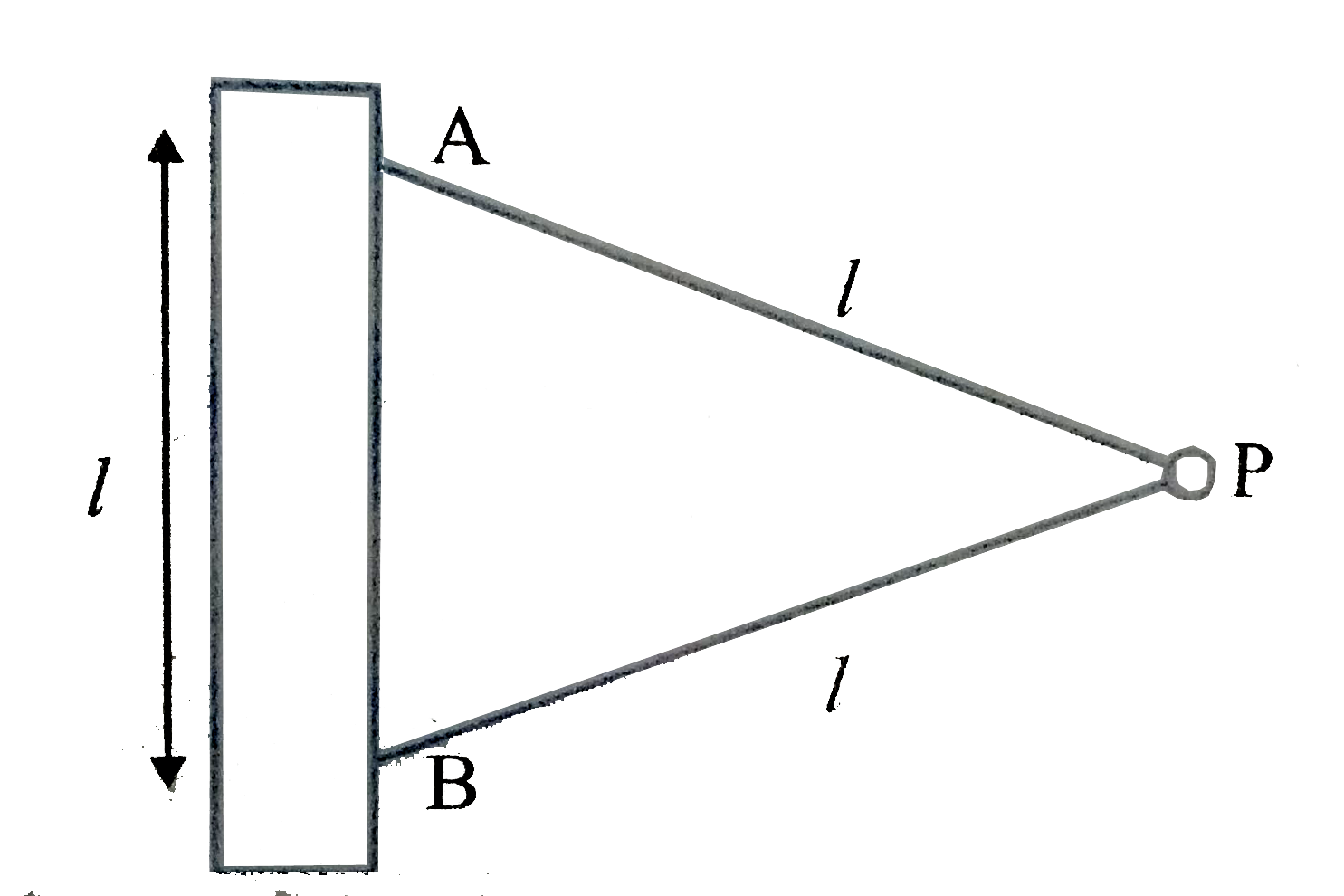
View SolutionA particle P of mass m is attached to a vertical axis by two strings AP and BP of legth l each. The separation AB=l, rotates around the axis with an angular velocity ω. The tension in the two string are T1 and T2. Then
View Solution

