Two identical springs are attached to a small block P. The other ends of the springs are fixed at A and B, When P is in equilibrium the extension of bottom spring is 10 cm. The period of small vertical oscillations of P about is equilibrium position is (useg=9.8m/s2)

2π7sec
π7sec
2π5sec
none of these
The correct Answer is:B
Step by step video, text & image solution for Two identical springs are attached to a small block P. The other ends of the springs are fixed at A and B, When P is in equilibrium the extension of bottom spring is 10 cm. The period of small vertical oscillations of P about is equilibrium position is (use "g"=9.8 m//s^(2)) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Multiple Correct Answer Type
Explore 9 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Single correct anwer type
Explore 14 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBook:CENGAGE PHYSICSChapter:KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSExercise:Interger
Explore 11 Videos
- MISCELLANEOUS KINEMATICSBook:CENGAGE PHYSICSChapter:MISCELLANEOUS KINEMATICSExercise:Interger type
Explore 3 Videos
Similar Questions
A light pulley is suspended at the lower end of a spring of constant k1, as shown in figure. An inextensible string passes over the pulley. At one end of string a mass m is suspended, the other end of the string is attached to another spring of constant k2. The other ends of both the springs are attached to rigid supports, as shown. Neglecting masses of springs and any friction, find the time period of small oscillations of mass m about equilibrium position.

View Solution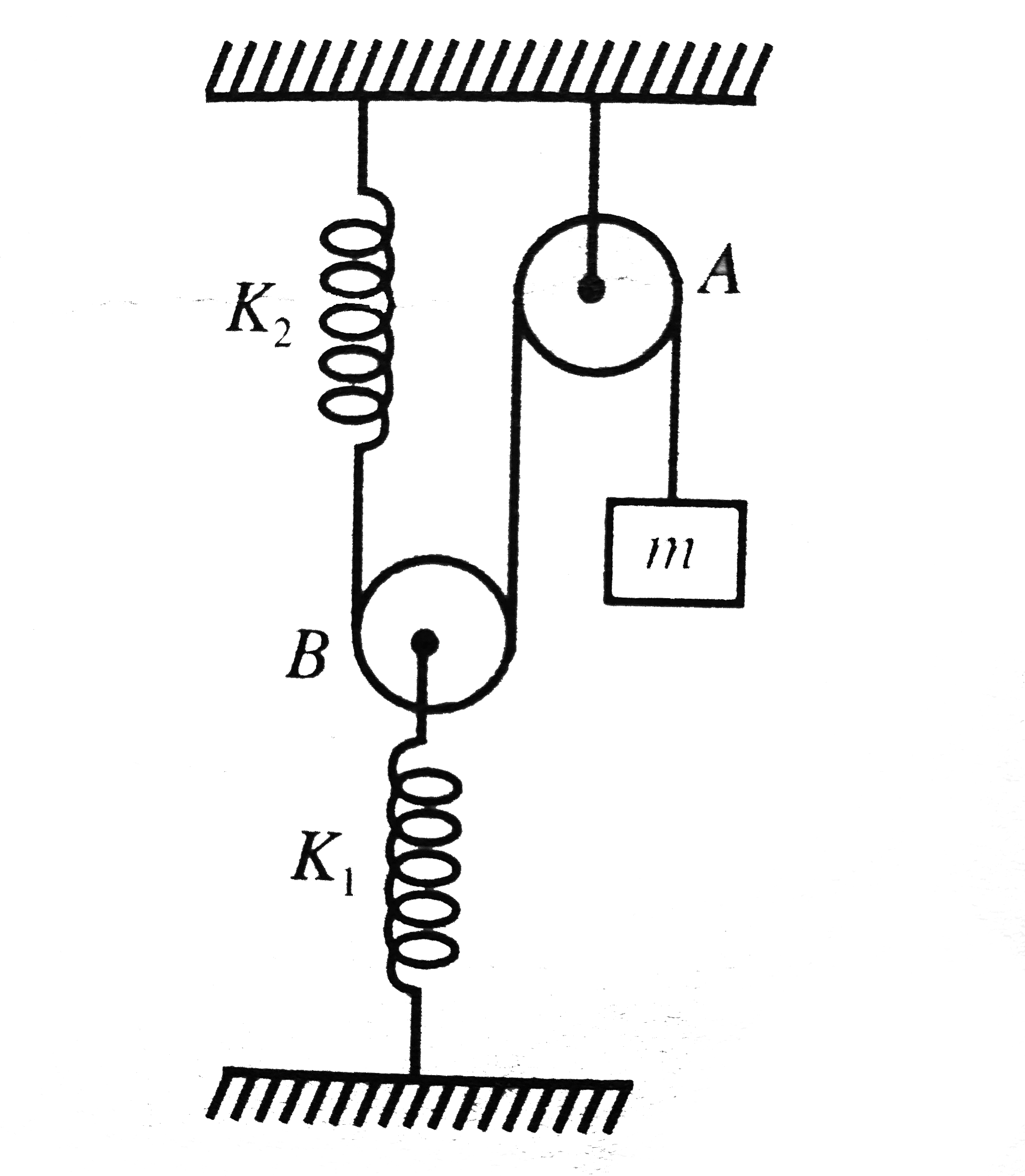
A block of mass m is tied to one end of a spring which passes over a smooth fixed pulley A and under a light smooth movable pulley B. The other end of the string is attached to the lower end of a spring of spring constant K2. Find the period of small oscillation of mass m about its equilibrium position (in second). (Take m=π2kg,K2k=4K1,K1=17Nm.)
View Solution
Knowledge Check
Two identical spring are attached to a small block P The other ends of the springs are fixed at A and B. when P is equilibrium the extension of top spring is 20cm and extension of bottom spring is 10cm The period at small vertical oscillation of p about its equilibrium position is (use g=9.8m/s2)
 A2π7secBπ7secC2π5secDnone of these
A2π7secBπ7secC2π5secDnone of theseIn the figure, a block of mass m is rigidly attached to two identical springs of stiffness k each. The other ends of the springs are connected to the fixed wall. When the block is in equilibrium, length of each spring is b, which is greater than the natural length of the spring. The time period of the oscillation of the block if it is displaced by small distance perpendicular to the length of the springs and released. Space is gravity free.
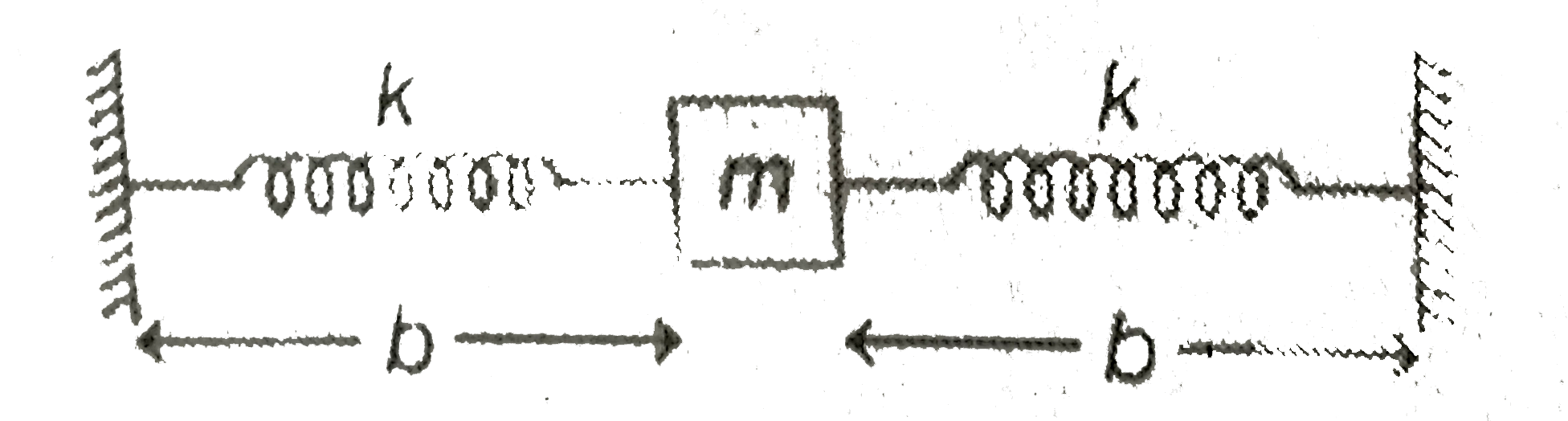 A2π√mbk(b−1)B2π√mb2k(b−l)C2π√(mb−lkb)D2π√(mb−l2kb)
A2π√mbk(b−1)B2π√mb2k(b−l)C2π√(mb−lkb)D2π√(mb−l2kb)
Find the elastic potential energy stored in each spring shown in figure, when the block is in equilibrium. Also find the time period of vertical oscillation of the block.

View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is

View SolutionConsider a block symmetrically attached to two.identical massless springs by means of strings passing over light frictionless pulleys as shown in.the figure. In the equilibrium position extension in each spring is 0.5m. The time period of small vertical oscillation of the block is T second. Find the value of 5√3πT.
'(##CEN_KSR_PHY_JEE_C16_E01_027_Q11##)'
View SolutionConsider a block symmetrically attached to two identical massless springs by means of strings passing over light frictionless pulleys as shown. In the equilibrium position extension in the springs is x0. Find the time period of small vertically oscillations of the blocks.
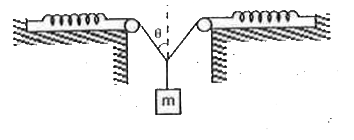
View SolutionA rod of length l and mass m, pivoted at one end, is held by a spring at its mid - point and a spring at far end. The spring have spring constant k. Find the frequency of small oscillations about the equilibrium position.

View SolutionTwo identical springs of spring constant '2k' are attached to a block of mass m and to fixed support (see figure).When the mass is displaced from equilibrium position on either side, it executes simple harmonic motion. The time period of oscillations of this sytem is :

View Solution

