The capacitor C1 in the figure initially carries a charge q0. When the switch S1 and S2 are shut, capacitor C1 is connected in series to a resistor R and a second capacitor C2, which initially does not carry any charge.
If the heat lost in the resistor after a long time of closing the switch is q20C2kC1(C1+C2), then Find the value of k.
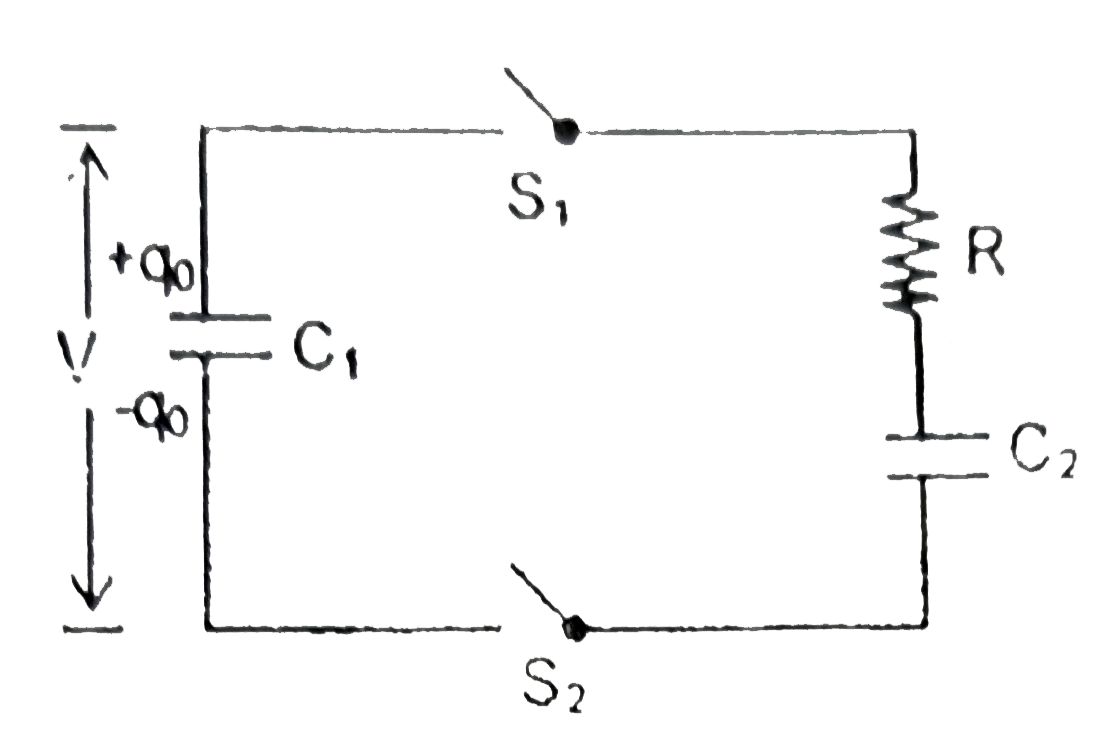
Step by step video & image solution for The capacitor C_(1) in the figure initially carries a charge q_(0). When the switch S_(1) and S_(2) are shut, capacitor C_(1) is connected in series to a resistor R and a second capacitor C_(2), which initially does not carry any charge. If the heat lost in the resistor after a long time of closing the switch is (q_(0)^(2)C_(2))/(kC_(1)(C_(1)+C_(2))), then Find the value of k. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
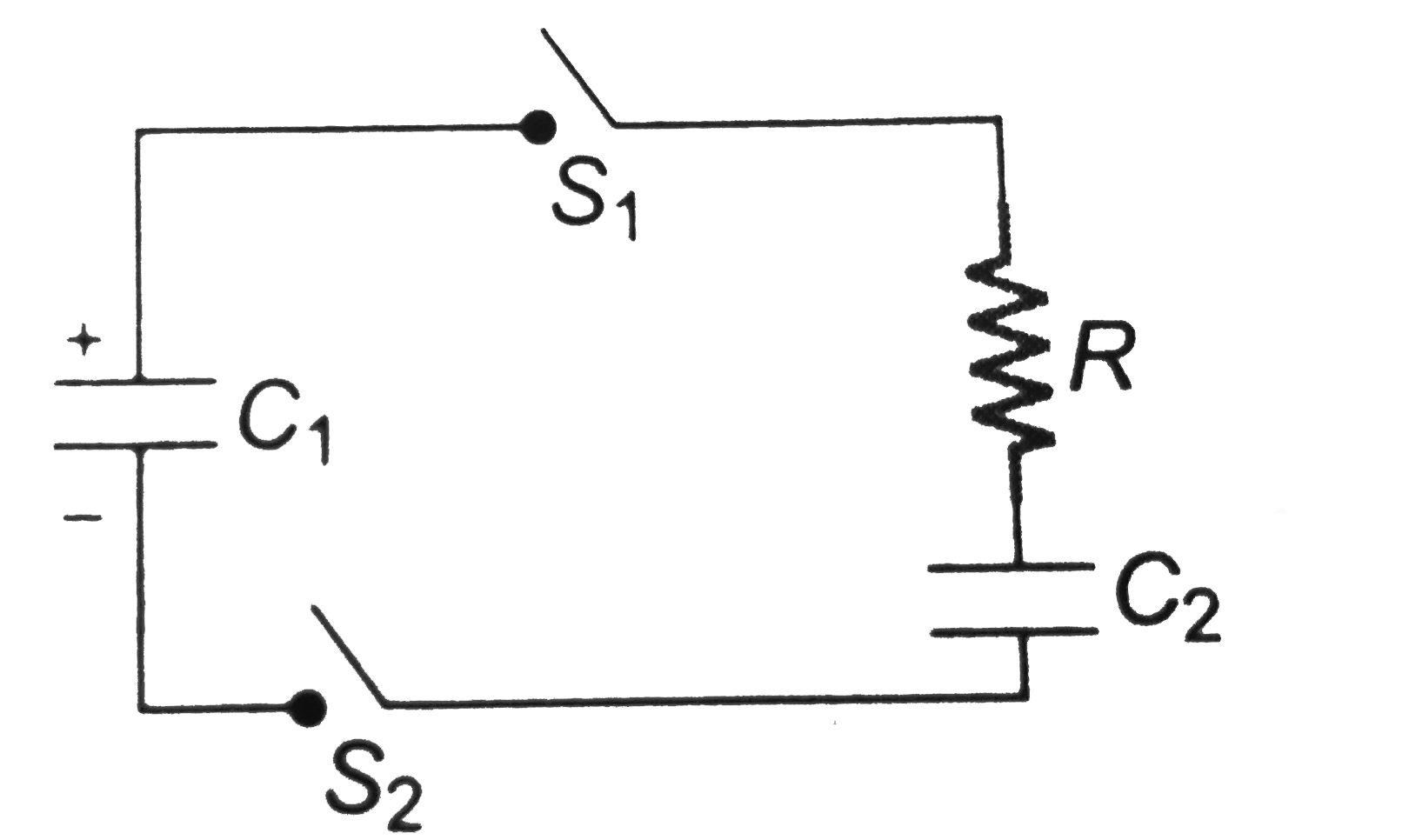
The capactor C1 in the figure initially carries a charge q0. When the i switch S1 and S2 are closed, capacitor C1 is connected to a resistor R and a second capacitor C2, which initially does not carry any charge.
(a) Find the charges deposited on the capacitors in steady state and the current through R as a function of time.
(b) What is heat lost in the resistor after a long time of closing the switch?
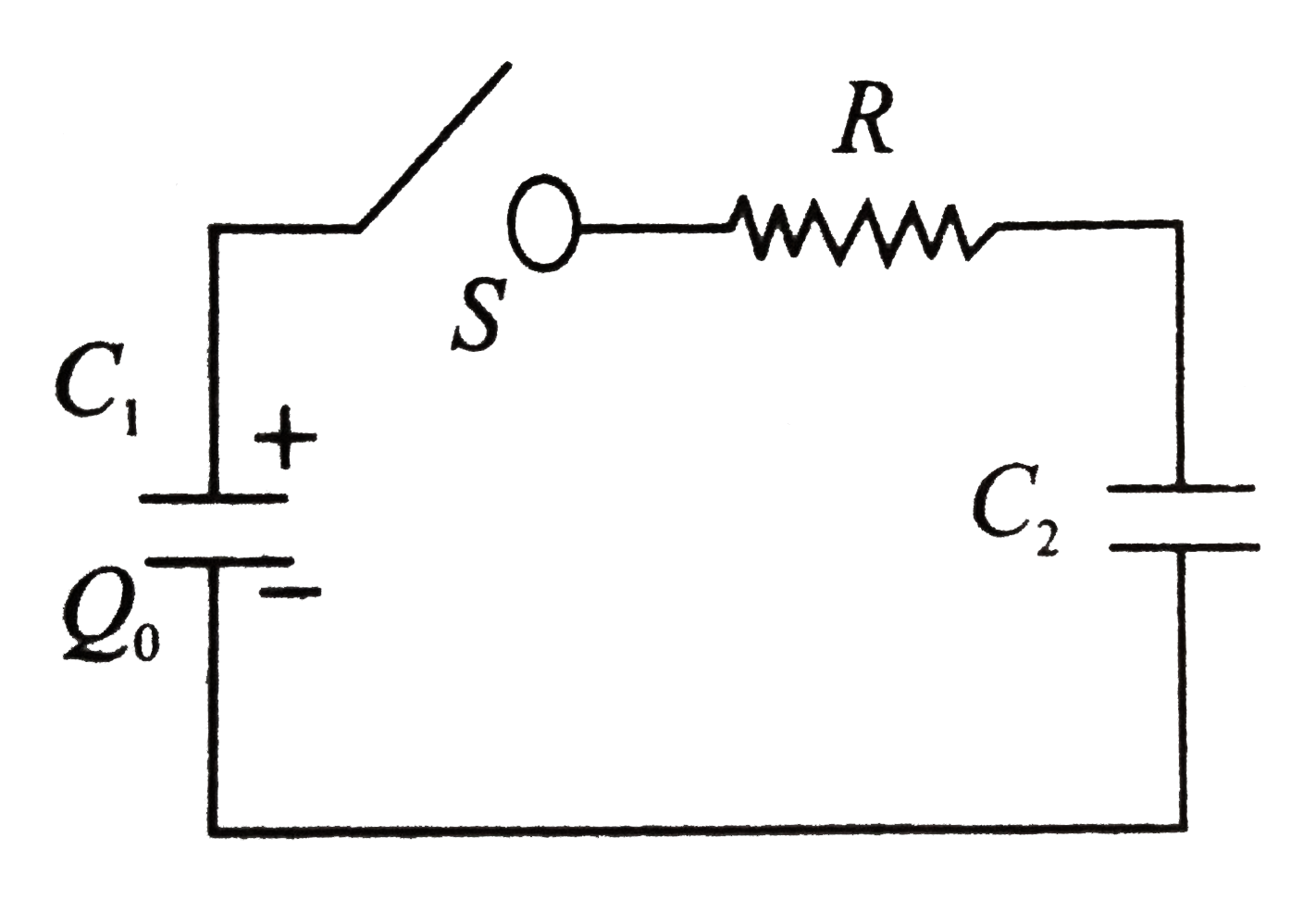
View SolutionIn the circuit shown, the capacitor C1 is initially charged with charge q0. The switch S is closed at time t = 0 . The charge on C2 after time t is
View Solution
Knowledge Check
The capacitor C1 in the figure shown initially carries a charge q0. When the switches S1 and S2 are closed, capacitor C1 is connected in series to a resistor R and a second capacitor C2 which is initially uncharged.
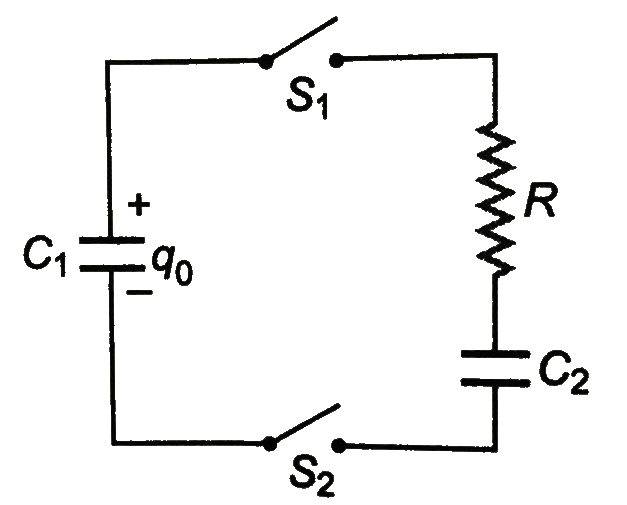
the total head dissipated in the circuit during the discharging process of C1 isAq202C21×CBq202CCq20C22C21Dq202C1C2The capacitor C1 in the figure shown initially carries a charge q0. When the switches S1 and S2 are closed, capacitor C1 is connected in series to a resistor R and a second capacitor C2 which is initially uncharged.

The charge flown through wires as a function of time is
where C=C1C2C1+C2Aq0e−tRC+CC2q0Bq0CC1x[1−e−tRC]Cq0CC1e−tCRDq0e−tRCIn the given figure switch is open initially and capacitor C2 is unchanged
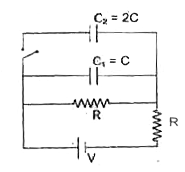
Charge on C2 just after closing the switch isACV2BCV3CCV4DCV8
Two capacitor C1 and C2, charged with chargesq1 and q2 then these are connected in series with an uncharged capacitor C, as shown in figure. As the switch S is closed :
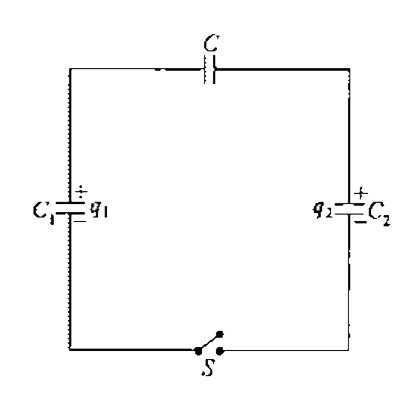
View SolutionIn the given LC circuit if initially capacitor C has change Q on it and 2C has charge 2Q. The polarities are as shown in the figure. Then after closing the switch s at t=0

View SolutionA 10V battery is connected to two capacitors C1 and C2 and a resistor R. When the capacitors are fully charged, then the potential difference across the resistor will be
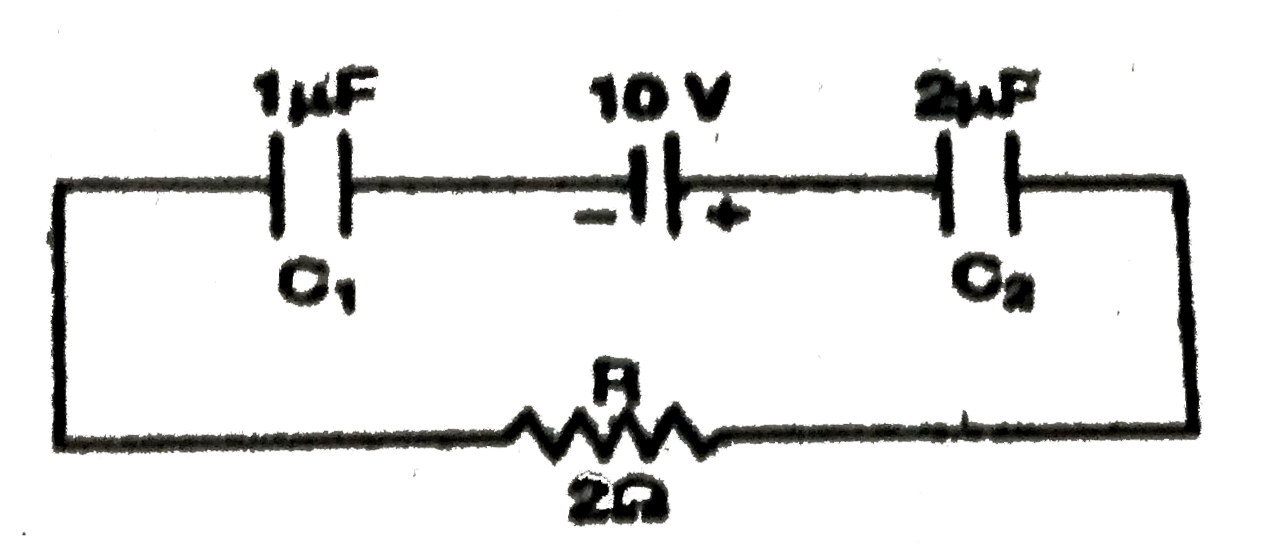
View SolutionIn the given figure switch is open initially and capacitor C2 is unchanged

Potential difference on C1just after closing the switch is
View SolutionA capacitor C is connected to a battery circuit having two switches S1 and S2 and resistances R1 and R2. The capacitor will be fully charged when
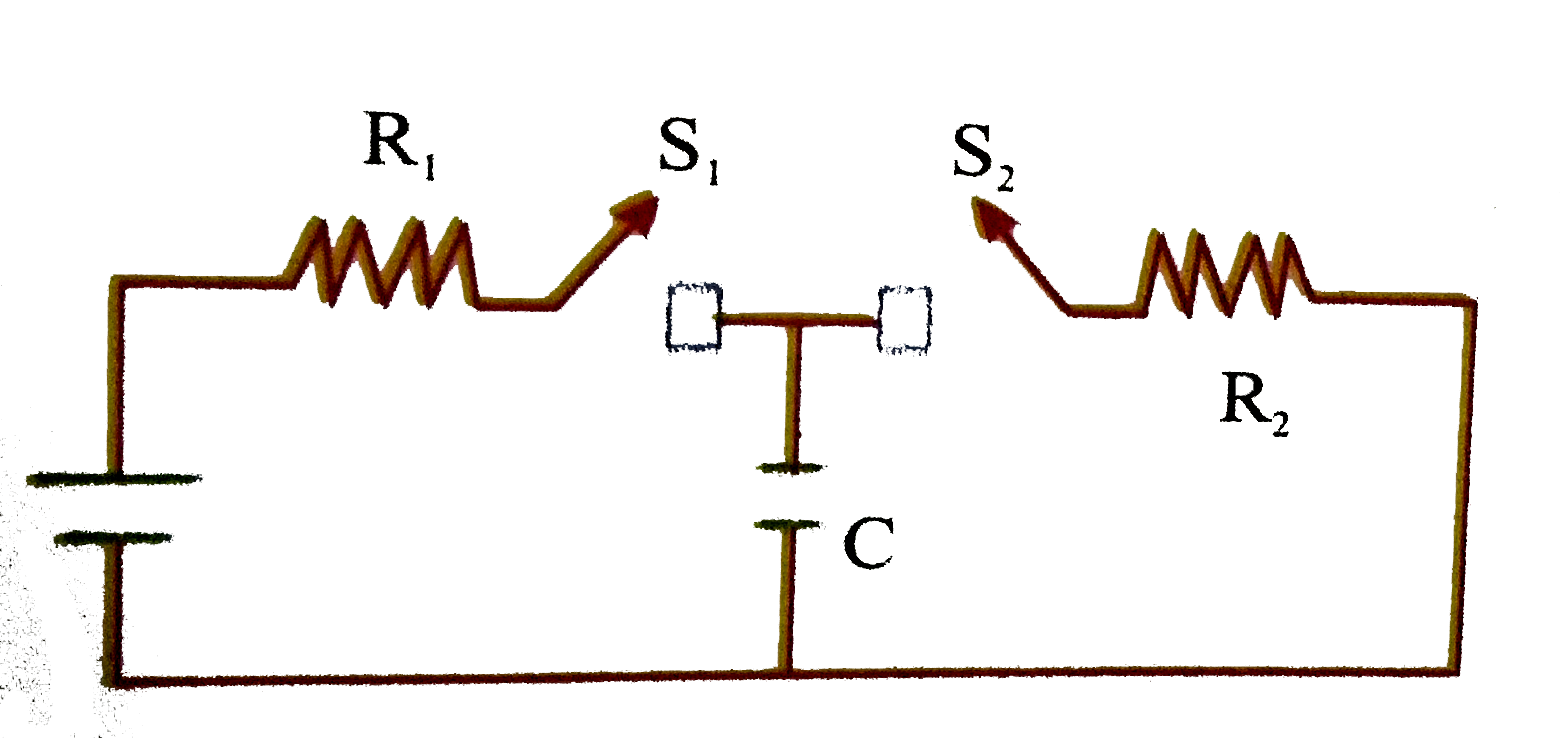 .
.
View Solution
