A particle executes simple harmonic motion along a straight line with an amplitude A . The potential energy is maximum when the displacement is
zero
The correct Answer is:A
To solve the question, we need to determine the displacement of a particle executing simple harmonic motion (SHM) when its potential energy is at a maximum.
1. Understanding Simple Harmonic Motion (SHM):
- In SHM, a particle oscillates back and forth around an equilibrium position. The maximum displacement from this equilibrium position is called the amplitude (A).
2. Energy in SHM:
- In SHM, the total mechanical energy (E) is conserved and is the sum of kinetic energy (KE) and potential energy (PE).
- The relationship can be expressed as:
E=KE+PE
- Kinetic energy is given by:
KE=12mv2
- Potential energy in SHM is given by:
PE=12kx2
where k is the spring constant and x is the displacement from the mean position.
3. Condition for Maximum Potential Energy:
- Potential energy is maximum when kinetic energy is minimum. The minimum value of kinetic energy occurs when the particle momentarily stops, which means its velocity (v) is zero.
4. Finding the Displacement:
- The velocity is zero at the extreme positions of the motion, which are at x=+A and x=−A.
- Therefore, the displacement at which the potential energy is maximum is when the particle is at the amplitude positions:
x=+Aorx=−A
5. Conclusion:
- The potential energy is maximum when the displacement is either at the positive amplitude A or the negative amplitude −A.
Final Answer:
The potential energy is maximum when the displacement is x=+A or x=−A.
---
- In SHM, a particle oscillates back and forth around an equilibrium position. The maximum displacement from this equilibrium position is called the amplitude (A).
- In SHM, the total mechanical energy (E) is conserved and is the sum of kinetic energy (KE) and potential energy (PE).
- The relationship can be expressed as:
E=KE+PE
- Kinetic energy is given by:
KE=12mv2
- Potential energy in SHM is given by:
PE=12kx2
where k is the spring constant and x is the displacement from the mean position.
- Potential energy is maximum when kinetic energy is minimum. The minimum value of kinetic energy occurs when the particle momentarily stops, which means its velocity (v) is zero.
- The velocity is zero at the extreme positions of the motion, which are at x=+A and x=−A.
- Therefore, the displacement at which the potential energy is maximum is when the particle is at the amplitude positions:
x=+Aorx=−A
- The potential energy is maximum when the displacement is either at the positive amplitude A or the negative amplitude −A.
The potential energy is maximum when the displacement is x=+A or x=−A.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:ERRORLESS Chapter:SIMPLE HARMONIC MOTIONExercise:Time period and frequency
Explore 18 Videos
- SIMPLE HARMONIC MOTIONBook:ERRORLESS Chapter:SIMPLE HARMONIC MOTIONExercise:simple pendulum
Explore 61 Videos
- SIMPLE HARMONIC MOTIONBook:ERRORLESS Chapter:SIMPLE HARMONIC MOTIONExercise:Acceleration of simple Harmonic motion
Explore 21 Videos
- ROTATIONAL MOTIONBook:ERRORLESS Chapter:ROTATIONAL MOTIONExercise:Practice Problems (Problems based on motion of connected mass)
Explore 10 Videos
- SURFACE TENSIONBook:ERRORLESS Chapter:SURFACE TENSIONExercise:Exercise
Explore 214 Videos
Similar Questions
Knowledge Check
While a particle executes linear simple harmonic motion
Aits linear velocity and acceleration pass through their maximum and minimum values once in each oscillation.BIts linear velocity and acceleration pass through their maximum and minimum values twice in each oscillation.Cits linear velocity and acceleration pass through their maximum and minimum values four times in each oscillation.Dits linear velocity and acceleration always attain their peak values simlataneaously.A particle is executing linear simple harmonic motion of amplitude 'A'. The fraction of the total energy is the kinetic when the displacement is half of the amplitude is
A14B12√2C12D34If a particle is executing simple harmonic motion, then acceleration of particle
Ais uniformBvaries linearly with timeCis non uniformDBoth (2) & (3)
The variation of displacement with time of a particle executing free simple harmonic motion is shown in the figure.
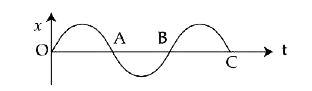
The potential energy U(x) versus time (t) plot of the particle is correctly shown in figure :
View SolutionA particle executes simple harmonic motion with a frequency f. The frequency with which the potential. Energy oscillates is
View SolutionThe phase of a particle executing simple harmonic motion is π2 when it has
View SolutionA particle executes simple harmonic motion with a of period of 6 s and amplitude of 3 cm. Its maximum speed (in cm/s) i
View SolutionA particle is executing simple harmonic motion with an amplitude of 0.02 metre and frequency 50 Hz . The maximum acceleration of the particle is
View Solution

