A cell is connected between two points of a uniformly thick circular conductor. The magnetic field at the centre of the loop will be
(Here and are the currents flowing in the two parts of the circular conductor of radius and has the usual meaning)
Zero
The correct Answer is:A
To find the magnetic field at the center of a uniformly thick circular conductor with two different currents flowing in opposite directions, we can follow these steps:
1. Understanding the Setup:
- We have a circular conductor of radius 'a'.
- There are two segments of the conductor carrying currents i1 and i2 in opposite directions.
- The magnetic field at the center of the loop needs to be calculated.
2. Magnetic Field Due to a Circular Loop:
- The magnetic field B at the center of a circular loop carrying current I is given by the formula:
B=μ0I2a
- Here, μ0 is the permeability of free space, and a is the radius of the loop.
3. Calculating Magnetic Fields for Each Segment:
- For the segment carrying current i1, the magnetic field at the center is:
B1=μ0i12a
- For the segment carrying current i2, the magnetic field at the center is:
B2=μ0i22a
4. Direction of Magnetic Fields:
- The direction of the magnetic field due to i1 can be determined using the right-hand rule. If i1 is flowing in a clockwise direction, B1 will be directed into the plane.
- Conversely, if i2 is flowing in a counterclockwise direction, B2 will be directed out of the plane.
5. Net Magnetic Field Calculation:
- Since B1 and B2 are in opposite directions, the net magnetic field Bnet at the center is:
Bnet=B1−B2
- Substituting the expressions for B1 and B2:
Bnet=μ0i12a−μ0i22a
- This simplifies to:
Bnet=μ02a(i1−i2)
6. Final Result:
- The magnetic field at the center of the loop is given by:
Bnet=μ02a(i1−i2)
- We have a circular conductor of radius 'a'.
- There are two segments of the conductor carrying currents i1 and i2 in opposite directions.
- The magnetic field at the center of the loop needs to be calculated.
- The magnetic field B at the center of a circular loop carrying current I is given by the formula:
B=μ0I2a
- Here, μ0 is the permeability of free space, and a is the radius of the loop.
- For the segment carrying current i1, the magnetic field at the center is:
B1=μ0i12a
- For the segment carrying current i2, the magnetic field at the center is:
B2=μ0i22a
- The direction of the magnetic field due to i1 can be determined using the right-hand rule. If i1 is flowing in a clockwise direction, B1 will be directed into the plane.
- Conversely, if i2 is flowing in a counterclockwise direction, B2 will be directed out of the plane.
- Since B1 and B2 are in opposite directions, the net magnetic field Bnet at the center is:
Bnet=B1−B2
- Substituting the expressions for B1 and B2:
Bnet=μ0i12a−μ0i22a
- This simplifies to:
Bnet=μ02a(i1−i2)
- The magnetic field at the center of the loop is given by:
Bnet=μ02a(i1−i2)
Topper's Solved these Questions
Similar Questions
A cell is connected across two points P and Q of a uniform circular conductor, figure. Prove that the magnetic field at its centre O will be zero.
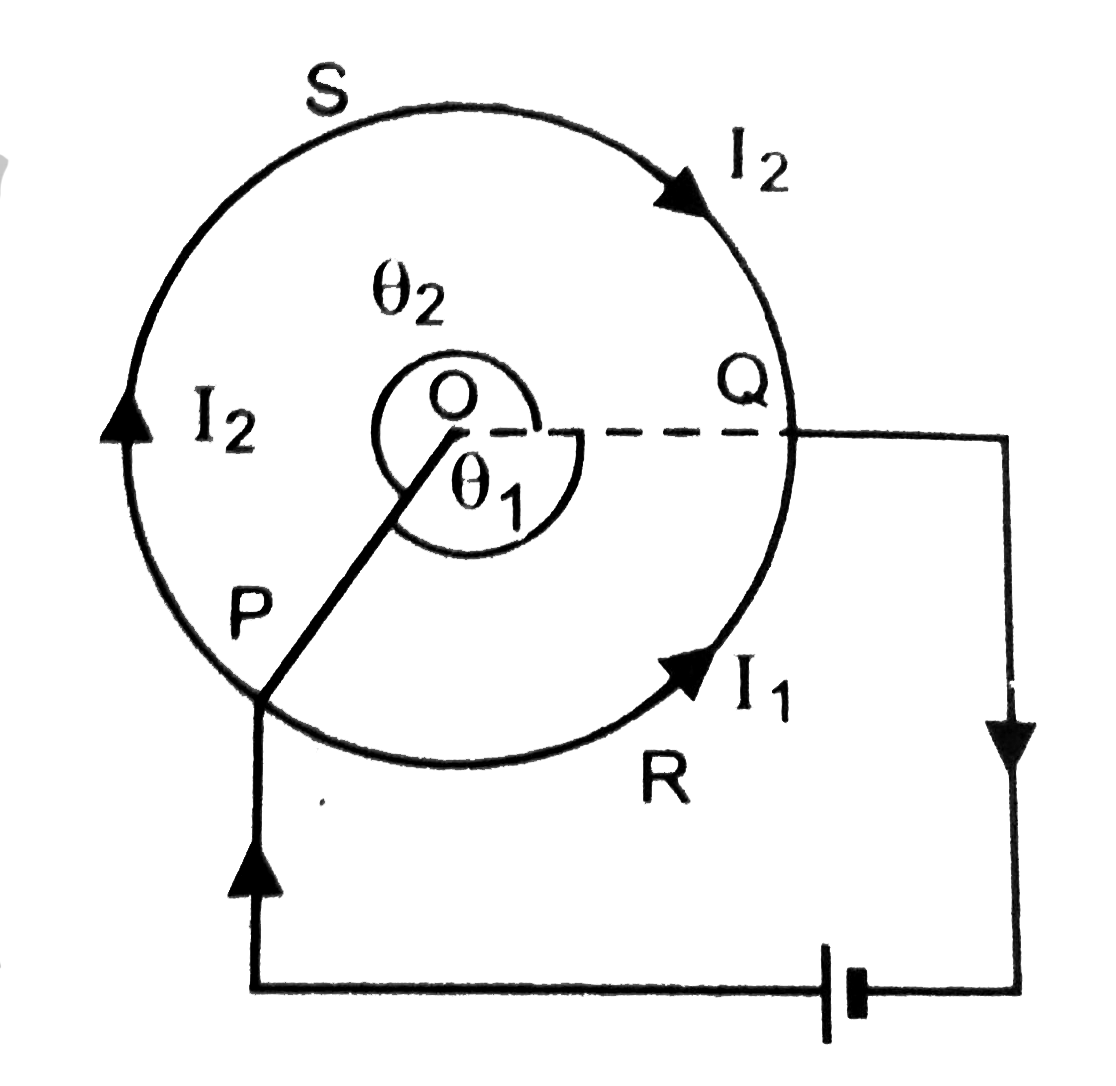
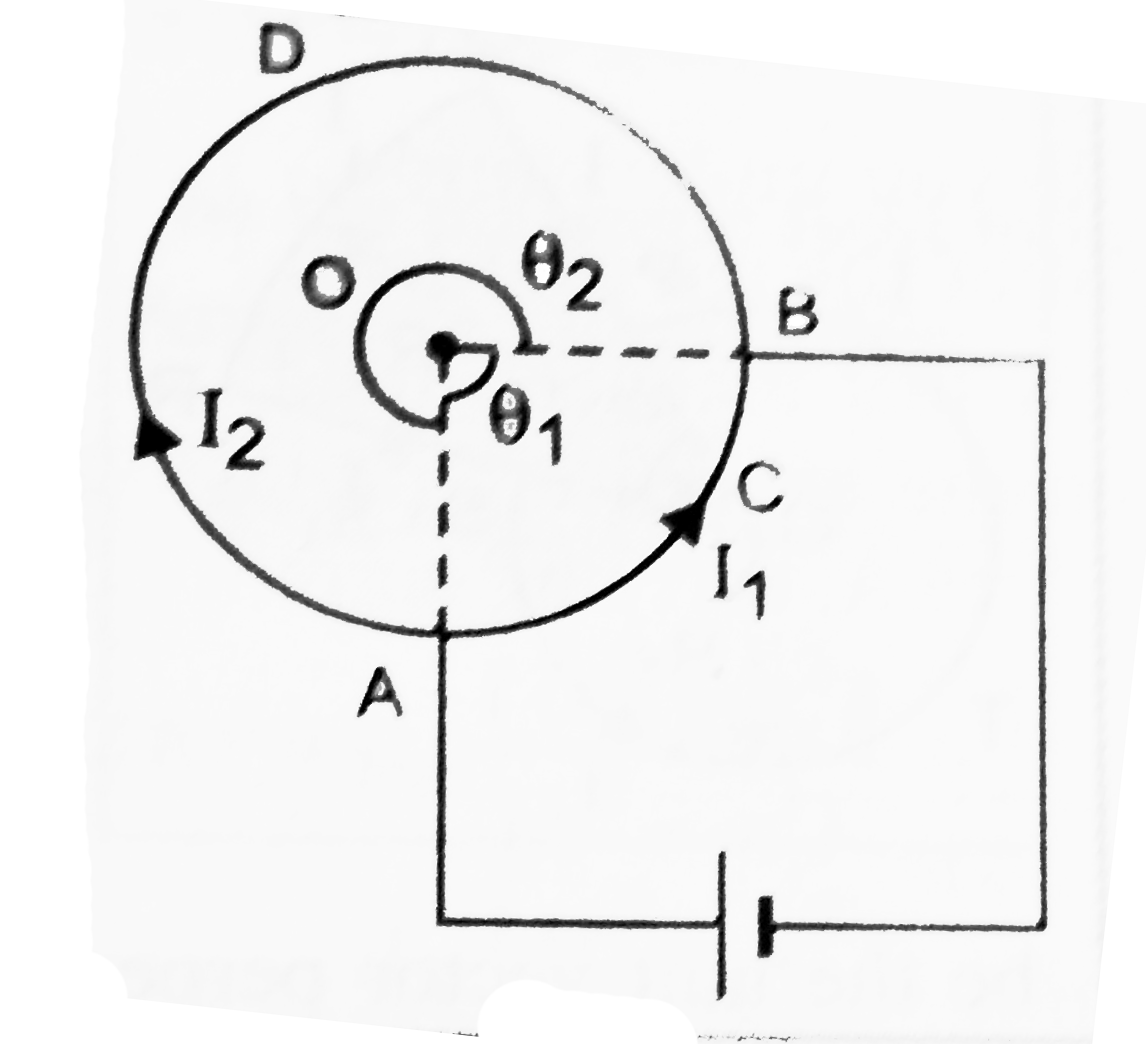
View SolutionAs shown in figure a cell is connected across two points A and B of a uniform circular conductor of radius r. Prove that the magnetic field induction at its centre O will be zero.
View Solution
Knowledge Check
A cell is connected between two points of a uniformly thick circular conductor and i1andi2 are the currents flowing in two parts of the circular conductor of radius a The magnetic field at the centre of the loop will be
AzeroBμ04π(I1−I2)Cμ02a(I1+I2)Dμ0a(I1+I2)A circular loop of radius 0.0157 m carriesa current of 2.0 A. The magnetic field at the centre of the loop is
A1.57×10−5Wb/m2B8.0×10−6Wb/m2C2.5×10−5Wb/m2D3.14×10−5Wb/m2To produce a magnetic field of π tesla at the centre of circular loop of diameter 1 m, the current flowing through loop is :
A5×106AB107AC2.5×106AD2×106A
A circular loop of radius 9.7 cm carries a current 2.3 A. Obtain the magnitude of the magnetic field at the centre of the loop .
View SolutionA circular conductor of radius 5cm produces a magnetic field of 7×10−6T at its centre. The current flowing through the conductor is: ?
View SolutionMagnetic field at the centre of a circular loop with n turns is 0.50 mt. Calculate the value of n if current of 5.3 A flows in the loop and radius of loop is 2 cm.
View SolutionAs shown in figure a cell is connected across two points A and B of a uniform circular conductor of radius r. Prove that the magnetic field induction at its centre O will be zero.

View SolutionA long straight conductor carrying a current i is bent to form an almost complete circular loop of radius r on it. The magnetic field at the centre of the loop

View Solution

