A uniform wire is bent in the form of a circle of radius R. A current I enters at A and leaves at C as shown in the figure :
If the length ABC is half of the length ADC, the magnetic field at the centre O will be
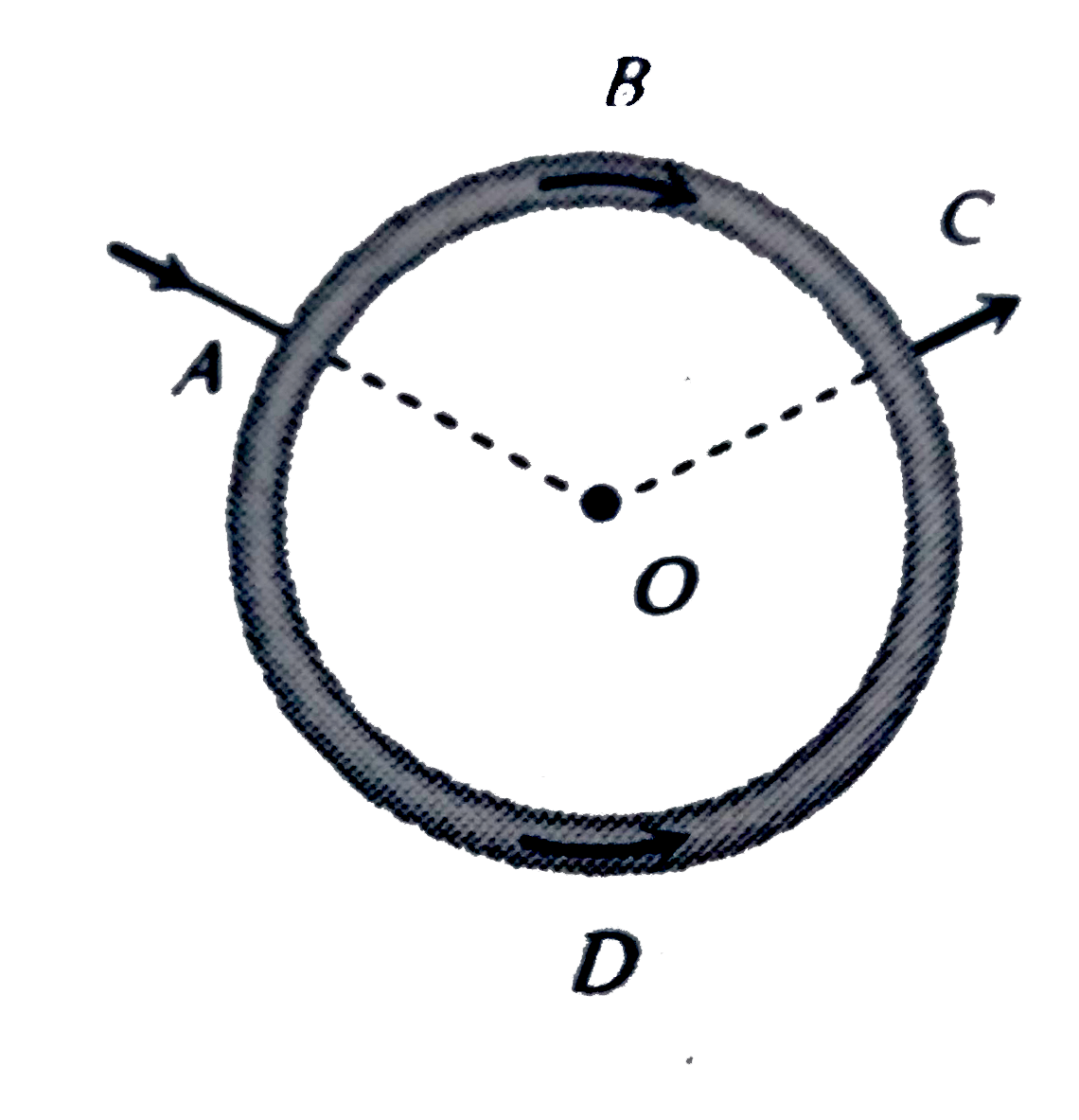
Zero
μ0I2R
μ0I4R
μ0I6R
The correct Answer is:A
Step by step video, text & image solution for A uniform wire is bent in the form of a circle of radius R. A current I enters at A and leaves at C as shown in the figure : If the length ABC is half of the length ADC, the magnetic field at the centre O will be by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
A long wire bent as shown in fig. carries current I. If the radius of the semicircular portion is a, the magnetic field at centre C is
 Aμ0I4aBμ0I4πa√π2+4Cμ0I4a+μ0I4πaDμ0I4πa√(π2−4)
Aμ0I4aBμ0I4πa√π2+4Cμ0I4a+μ0I4πaDμ0I4πa√(π2−4)A current carrying wire is bent in the L shapes as shown in figure. The length of both arms extend to infinity. Then, the magnetic field at O is-
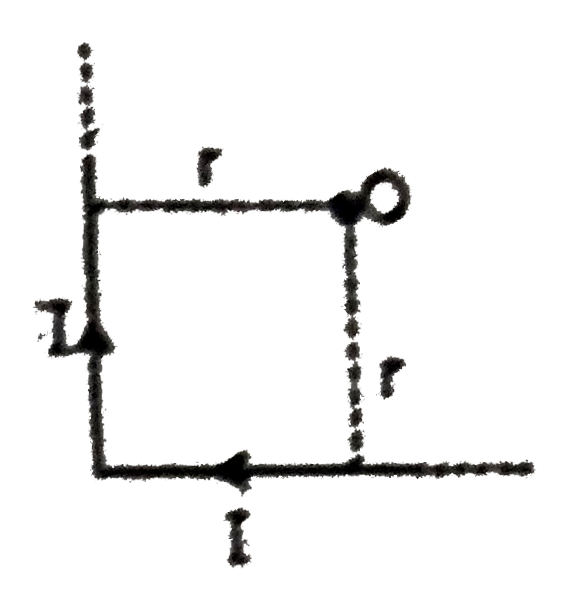 AzeroBμ0I/2πrCμ0I2πr(1+1√2)Dμ0I4πr(1+1√2)
AzeroBμ0I/2πrCμ0I2πr(1+1√2)Dμ0I4πr(1+1√2)A wire A , bent in the shape of an arc of a circle , carrying current of 2 and having radius 2 cm and another wire B, also bent in the shape of arc of a circle , carrying a current of 3 A and having radius of 4 cm , are placed as shown in the figure . The ratio of the magnetic fields due to the wires A and B at the common centre O is :
 A4:6B6:4C6:5D2:5
A4:6B6:4C6:5D2:5
A wire bent in the form of a sector of radius r subtending an angle θ∘ at centre as shown in figure is carrying a current I. The magnetic field at O is :
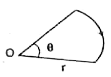
View SolutionA current carrying wire AB of the length L is turned along a circle, as shown in figure. The magnetic field at the centre O.

View SolutionThe resistance of wire ABC is double of resistance of wire ADC. The magnetic field at O is

View SolutionA charged wire is bent in the form of a semicircular arc of radius a. If charge per unit length is λ coulomb/metre, the electric field at the centre O is
View SolutionA conducting wire of length L is bent in the form of an equilateral triangle. If current I is made to pass through it, then calculate the magnetic field intensity at the centre of the triangle.
View Solution