A uniform conducting ring of mass π kg and radius 1 m is kept on smooth horizontal table. A uniform but time varying magnetic field B=(ˆi+t2ˆj)T is present in the region, where t is time in seconds. Resistance of ring is 2(Ω). Then
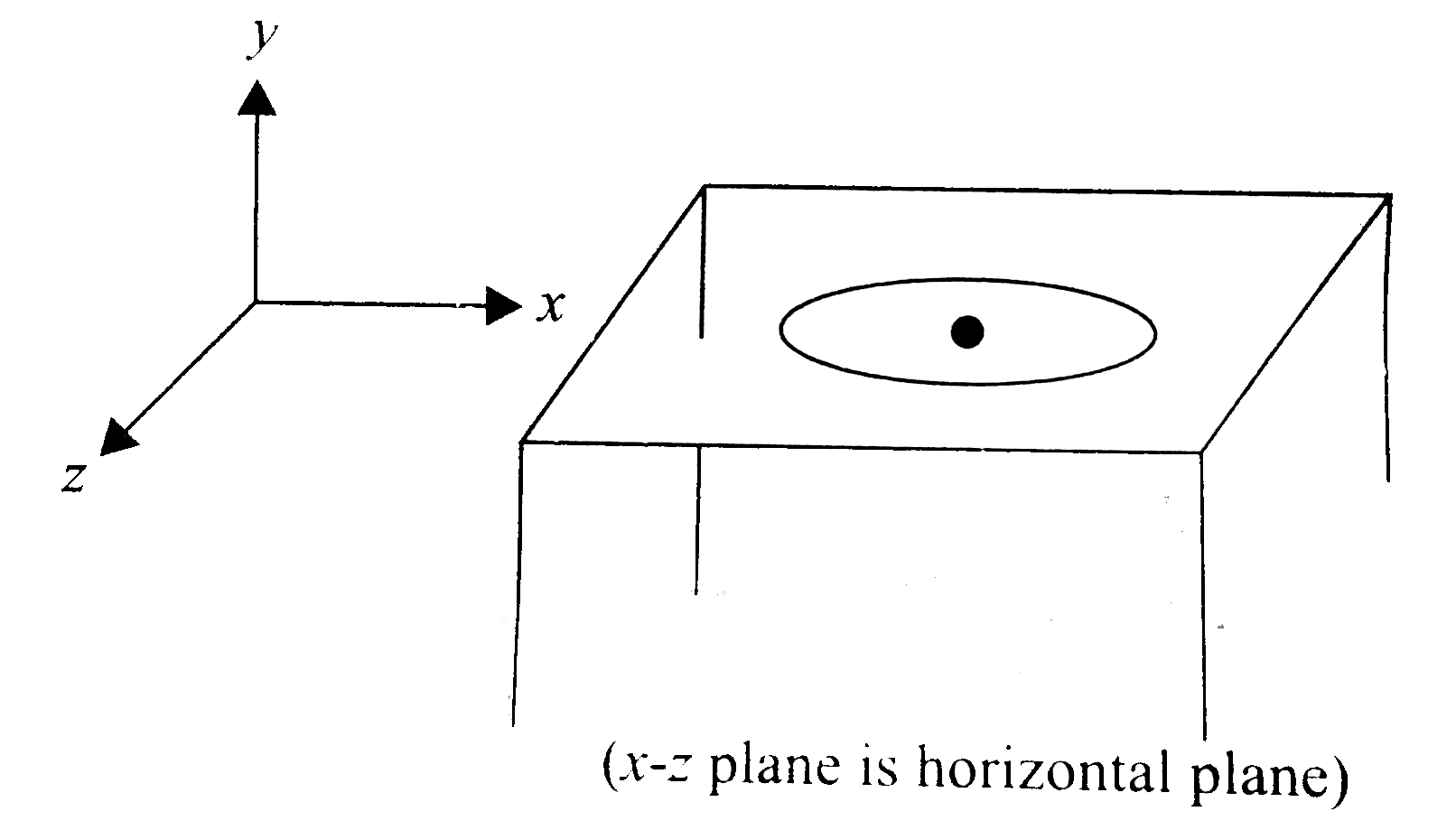
Heat generated (in kJ) through the ring till the instant when ring start toppling is
13πkJ
2πkJ
23πkJ
1πkJ
The correct Answer is:C
Heat generated
H=∫10/π0I2Rd=∫10/π0π2t2×2×dt
=20003πJ=23πkJ
Similar Questions
A conducting ring of mass 2 kg and radius 0.5 m is placed on a smooth horizontal plane. The ring carries a current 4A . A horizontal magnetic field B = 10T is switched on at time t = 0 as shown in figure. The initial angular acceleration of the ring will be:

View SolutionA conducting ring of mass m=πkg and radius R=12m is kept on a flat horizontal surface (xy plane). A uniform magnetic field is switched on in the region which changes with time (t) as →B=(2ˆj+t2ˆk)T. Resistance of the ring is r=πΩ and g=10ms−2.
(a) Calculate the induced electric field at the circumference of the ring at the instant it begins to topple.
(b) Calculate the heat generated in the ring till the instant it starts to topple.
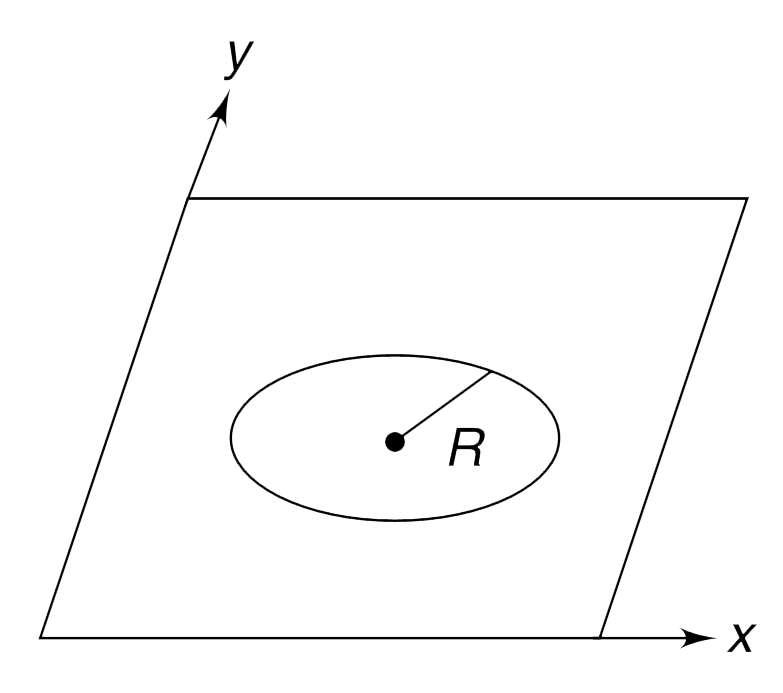
View Solution
Knowledge Check
A uniform conducting ring of mass π kg and radius 1 m is kept on smooth horizontal table. A uniform but time varying magnetic field B=(ˆi+t2ˆj)T is present in the region, where t is time in seconds. Resistance of ring is 2(Ω). Then
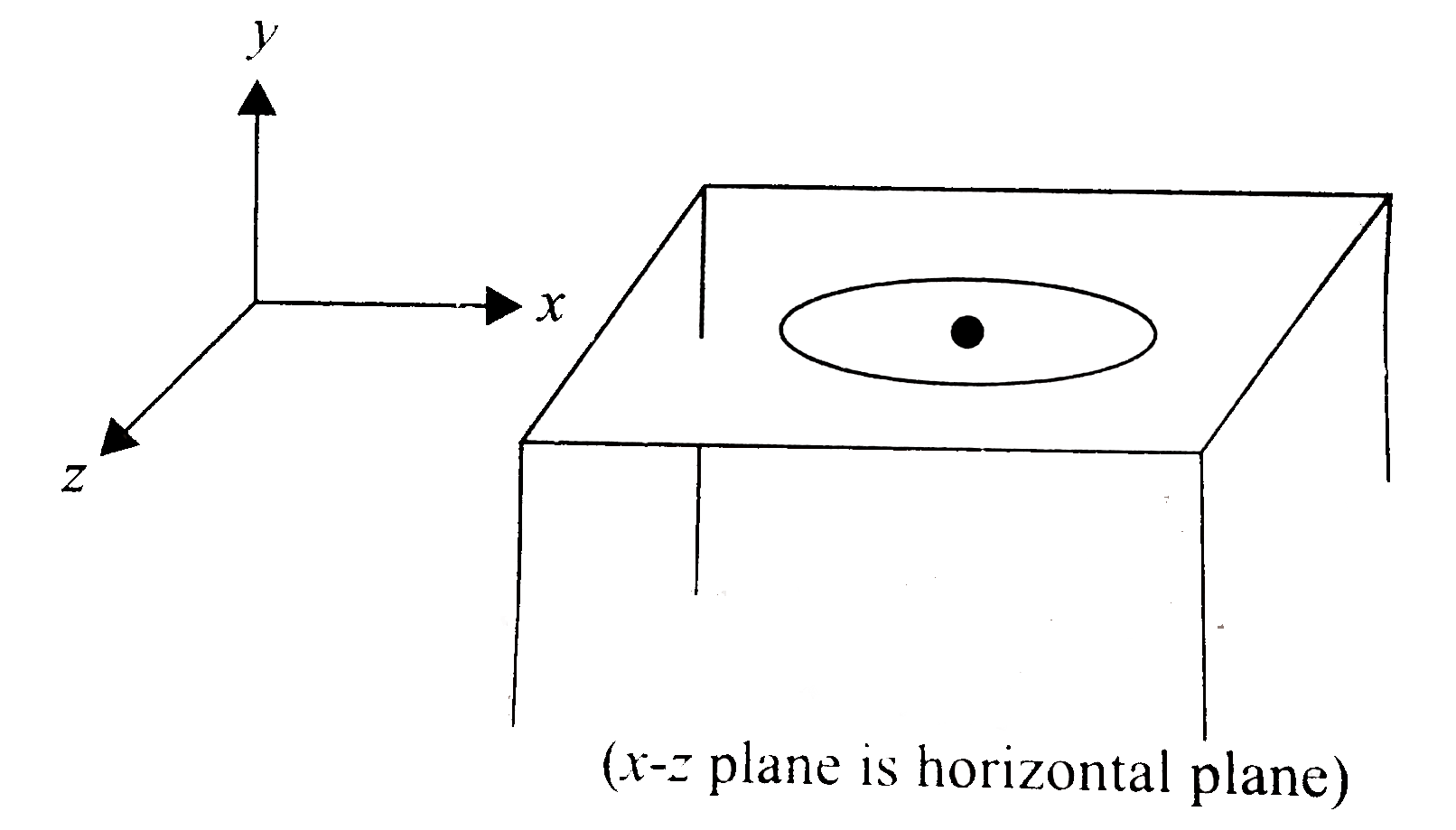
Time (in second) at which ring start toppling isA10πB20πC5πD25πA uniform conducting ring of mass π kg and radius 1 m is kept on smooth horizontal table. A uniform but time varying magnetic field B=(ˆi+t2ˆj)T is present in the region, where t is time in seconds. Resistance of ring is 2(Ω). Then
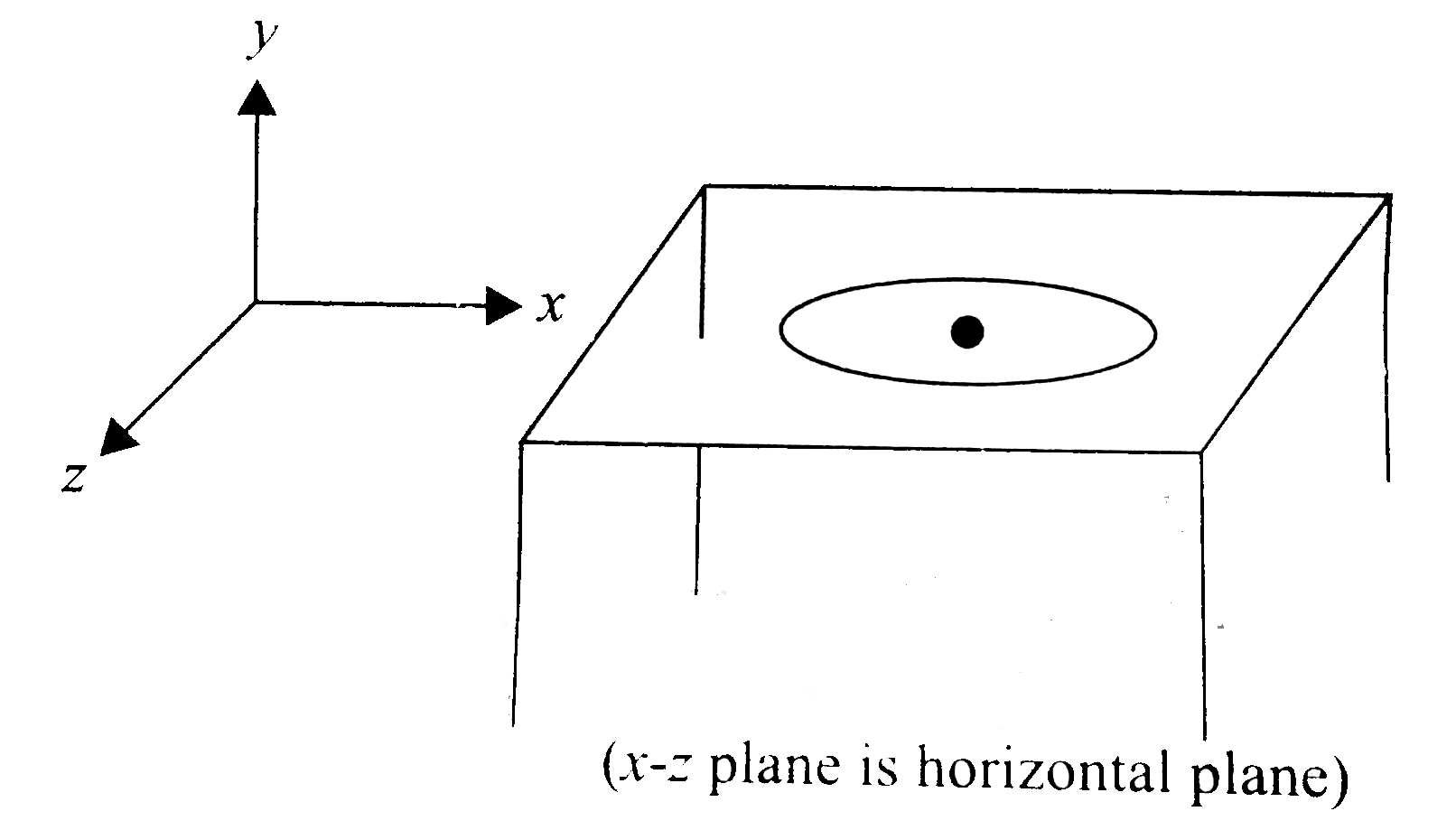
Net magnetic field (in Newton) on conducting ring as function of time isA2π2tB2π2t2C2π2t3DzeroA uniform conducting ring of mass π kg and radius 1 m is kept on smooth horizontal table. A uniform but time varying magnetic field B=(ˆi+t2ˆj)T is present in the region, where t is time in seconds. Resistance of ring is 2(Ω). Then
Induced electric field (in volt/meter) at the circumference of ring at the instant ring start toppling isA10πB20πC5πD25π
A conducting ring of radius r and resistance R is placed in region of uniform time varying magnetic field B which is perpendicular to the plane of the ring. It the magnetic field is changing at a rate α, then the current induced in the ring is
View SolutionA uniform conducting ring of mass m=2kg, radius r=2m and resistance 8Ω is kept on smooth, horizontal surface. A time varying magnetic field →B=(ˆi+t2ˆj) Tesla is present in the region, where t is time in second and take vertical as y-axis. (Take π2=10). Then
View SolutionA rectangular loop of sides of length l and b is placed in x-y plane. A uniform but time varying magnetic field of strength →B=20tˆi+10t2ˆj+50ˆk where t is time elapsed. The magnitude of induced emf at time t is:
View SolutionA conducting ring of mass 2kg and radius 0.5m is placed on a smooth plane. The ring carries a current of i=4A. A horizontal magnetic field B=10T is switched on at time t=0 as shown in fig The initial angular acceleration of the ring will be
 .
.
View SolutionA conducting rign of mass 100 gram and radius 0⋅5m is placed on a smooth horizontal plane. The ring carries a current of I=4A. A horizontal magnetic field B=10T is switched on at time t=0 as shown in figure. The initial angular acceleration of the ring is

View Solution
