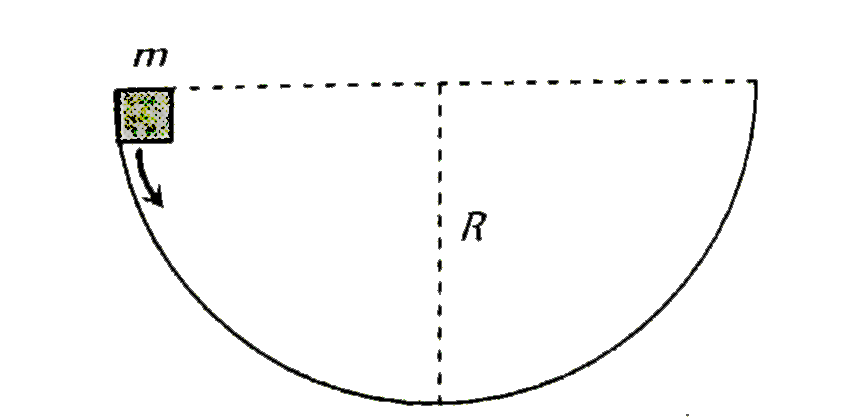
A mass m slips along the wall of a semispherical surface of radius R . The velocity at the bottom of the surface is
√Rg
√2Rg
2√πRg
√πRg
The correct Answer is:B
Step by step video, text & image solution for A mass m slips along the wall of a semispherical surface of radius R . The velocity at the bottom of the surface is by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MOTION IN ONE DIMENSIONBook:ERRORLESS Chapter:MOTION IN ONE DIMENSIONExercise:Critical Thinking
Explore 19 Videos
- MOTION IN ONE DIMENSIONBook:ERRORLESS Chapter:MOTION IN ONE DIMENSIONExercise:Graphical Questions
Explore 23 Videos
- MOTION IN ONE DIMENSIONBook:ERRORLESS Chapter:MOTION IN ONE DIMENSIONExercise:Relative Motion
Explore 13 Videos
- GRAVITATIONBook:ERRORLESS Chapter:GRAVITATIONExercise:SET
Explore 27 Videos
- MOTION IN TWO DIMENSIONBook:ERRORLESS Chapter:MOTION IN TWO DIMENSIONExercise:Exercise
Explore 319 Videos
Similar Questions
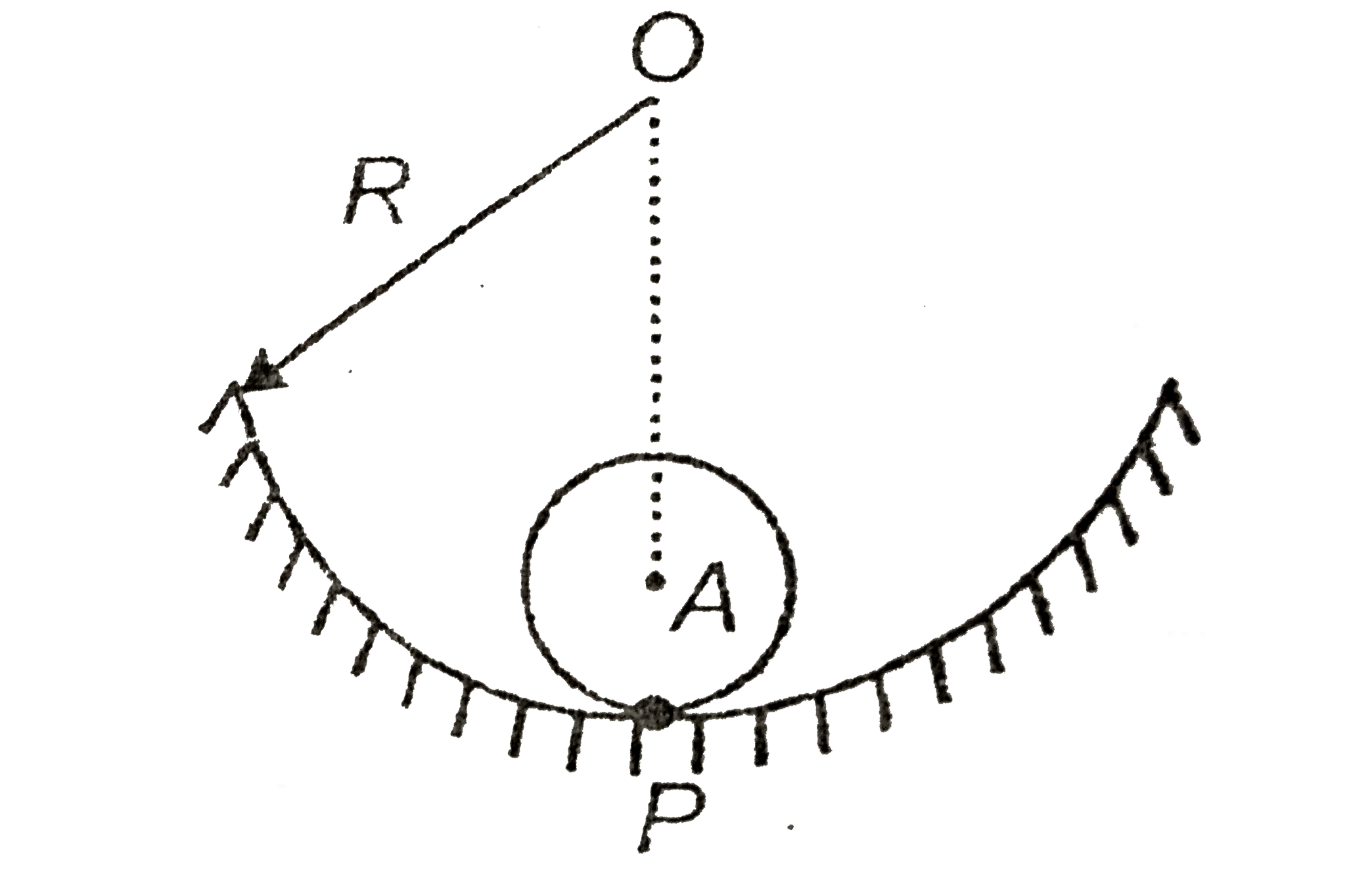
A sphere of radius r is rolling without slipping on a hemispherical surface of radius R. Angular velocity and angular acceleration of line OA is ω and α respectively. Find the acceleration of point P on sphere.
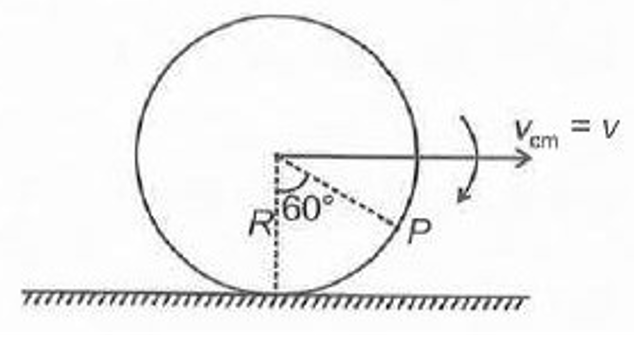
View SolutionA cycle tyre of mass M and radius R is in pure rolling over a horizontal surface. If the velocity of the centre of mass of the tyre is v, then the velocity of point P on the tyre, shown in figure is
View Solution
Knowledge Check
A mass m slips along the wall of a semispherical surface of radius R . The velocity at the bottom of the surface is
 A√RgB√2RgC√λRgD√λRg
A√RgB√2RgC√λRgD√λRgA body of mass m is placed at the centre of the spherical shell of radius R and mass M. The gravitation potential on the surface of the shell is
A−GH(M+m)B−GH(M−m)C−GH(mMM+m)D−GH(mMM−m)A block of mass M is being pulley along horizontal surface .The coefficient of friction the block and the surface is μ If another block of mass M/2 is placed on the block and it is pulled is again pulled on the surface , the coefficient of friction the block and the surface will be
AμB3μ2C2μD5μ2
A particle of mass m strikes elastically with a disc of radius R, with a velocity →v as shown in the figure. If the mass of the disc is equal to that of the particle and the surface of the contact is smooth, find the velocity of the disc just after the collision.

View SolutionA planet has mass equal to mass of the earth but radius one fourth of radius of the earth . Then escape velocity at the surface of this planet will be
View SolutionA block of mass m slides down along the surface of the bowl from the rim to the bottom as shown in fig. The velocity of the block at the bottom will be-

View SolutionInside a uniformly accelerating thin-walled spherical shell of radius R which is rolling on horizontal surface there is a small body slipping around Angle of friction between body and inner surface of sphere is 23∘ which of the following can be the acceleration a of the center of sphere to ensure that the small body stays at R/2 distance from the surface?

View SolutionAn earth satellite of mass m revolves in a circular orbit at a height h from the surface of the earth. R is the radius of the earth and g is acceleration due to gravity at the surface of the earth. The velocity of the satellite in the orbit is given by
View Solution

