Inside a uniformly accelerating thin-walled spherical shell of radius R which is rolling on horizontal surface there is a small body slipping around Angle of friction between body and inner surface of sphere is 23∘ which of the following can be the acceleration a of the center of sphere to ensure that the small body stays at R/2 distance from the surface?

g√3
3g4
gtan23∘
g√32
The correct Answer is:B
R is resultant of friction and normal reaction
Rsin53∘=mg
Rcos53∘=ma
⇒g(cos53∘sin53∘)=a
⇒a=g×cot53∘=3g/4
other possiblity R is resultant of friction and normal reaction
Rsin7∘=ma
Rcos7∘=ma
⇒g(cos7∘sin7∘)⇒a=g×cot7∘ (this option is not given)
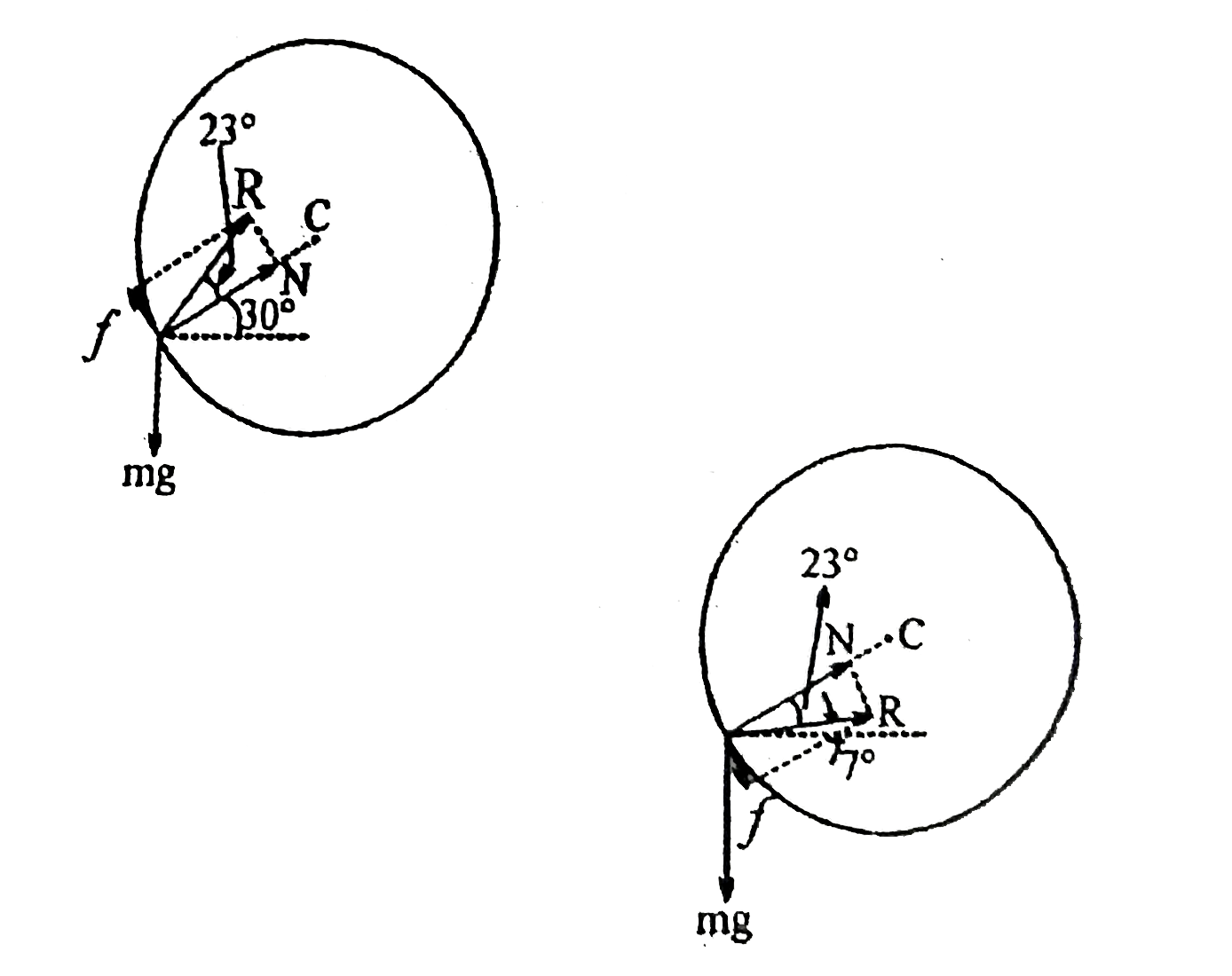
Topper's Solved these Questions
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Comphrehension
134 Videos
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Reasoning
75 Videos
- FLUID MECHANICSBOOK - BANSALCHAPTER - FLUID MECHANICSEXERCISE - PYQS AIEEE
10 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
The velocity- time graph of car moving on a straight track is given below. The car weight 1000kg.
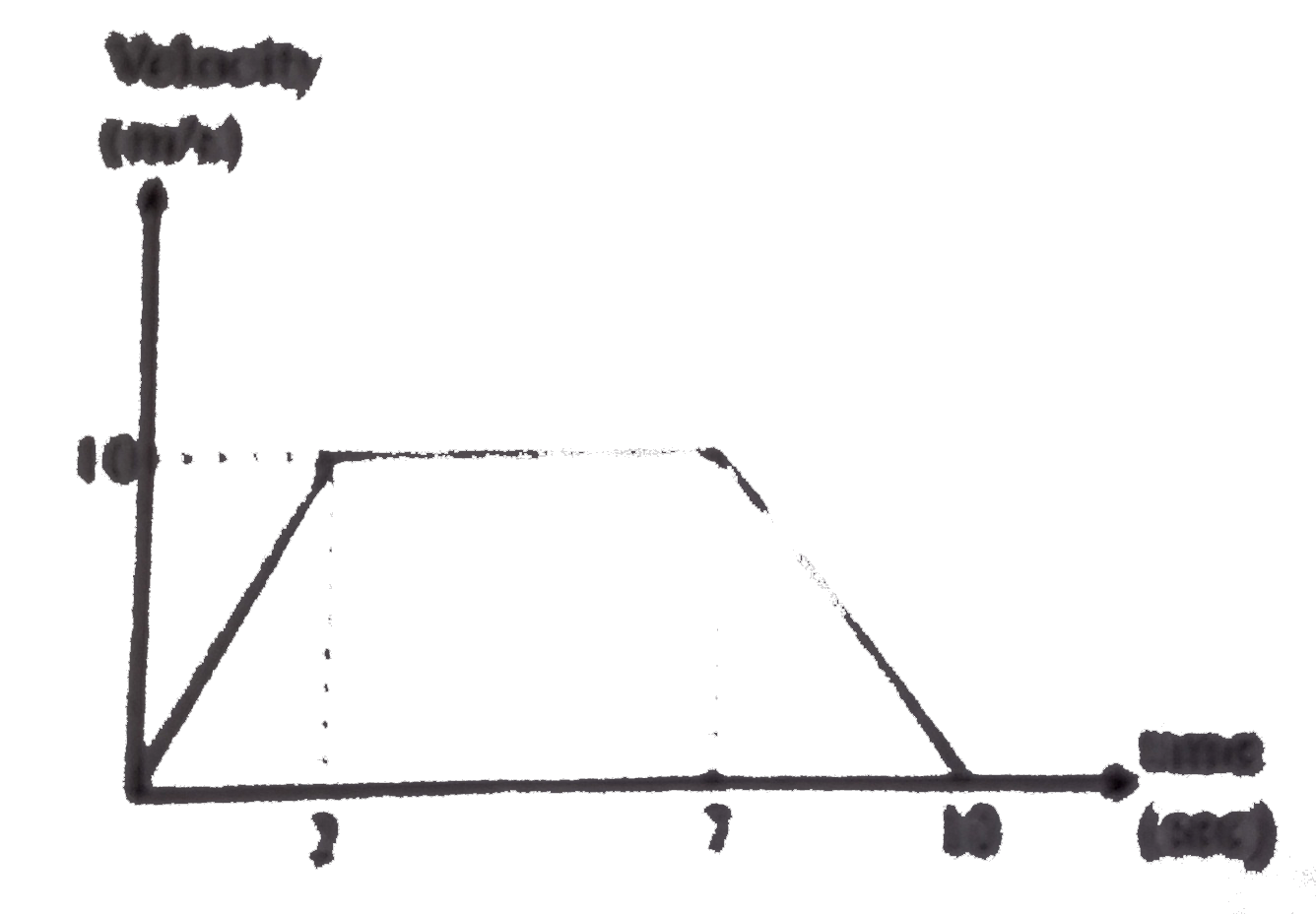 The distance travelled by the car during the whole motion is:
The distance travelled by the car during the whole motion is:
View SolutionStatement-1: The numerical value (n)of a physical quantity is inversely proportional to size of unit (u) being used to measure it.
Statement-2:The magnitude of physical quantity does not change by changing the units.
View SolutionA cylinder of height 20m is completely filled with water. The velocity of effux of water (∈ms−1) through a small hole on the side wall of the cylinder near its bottom is
View SolutionHow does the width of the depletion layer of a p-n junction diode change with decrease in reverse bias?
View SolutionA solid sphere rolling on a rough horizontal surface. Acceleration of contact point is zero. A solid sphere can roll on the smooth surface.
View SolutionA body is on a rough horizontal surface which is moving horizontally in SHM of frequency 2Hz. The coefficient of static friction between the body and the surface is 0.5. The maximum value of the amplitude for which the body will not slip along the surface is approximately
View SolutionA horizontal force is applied on a body on a rough horizontal surface produces an acceleration a .If coefficient of friction between the body and surface which is a is reduced to mu//3 ,the acceleration increses by 2 units .The value of mu is
View SolutionA small body of mass 'm' is placed at the top of a smooth sphere of radius 'R' placed on a horizontal surface as shown, Now the sphere is given a constant horizontal acceleration a_(0) = g . The velocity of the body relative to the sphere at the moment when it loses contact with the sphere is
View SolutionA solid sphere of mass M and radius R is covered with a thin shell of mass M. There is no friction between the inner wall of the shell and the sphere. The ball is released from rest, and then it rolls without slipping down an incline that is inclined at an angle theta to the horizontal. Find the acceleration of the ball.
View SolutionA small body of mass m slides without friction from the top of a hemisphere of radius r. At what height will the body be detached from the surface of hemisphere?

View SolutionA body moves on a horizontal circular road of radius of r, with a tangential acceleration a_(T) . Coefficient of friction between the body and road surface is mu . It begin to slip when it's speed is v , then :
View Solutionपृथ्वी ( त्रिज्या R) के पृष्ठ से 2R की दूरी पर पृथ्वी के आकर्षण के कारण एक पिण्ड का त्वरण होगा ( g = पृथ्वी के पृष्ठ पर गुरुत्वीय त्वरण ) :
View SolutionA horizontal force is applied on a body on a rough horizontal surface produces an acceleration ‘a’. If coefficient of friction between the body and surface which is μ is reduced to μ/3, the acceleration increases by 2 units. The value of 'μ' is
View SolutionA uniform solid sphere of radius R produces a gravitational acceleration of a_g on its surface. At what distance from the sphere's center are there points (a) inside and (b) outside the sphere where the gravitational acceleration is a_g /2?
View SolutionA small body is dropped into a narrow channel drilled along the Earth axis. Considering the Earth to be a homogeneous sphere and disregarding air resistance answer the following questions. (Acceleration due gravity on the surface of the Earth is g, Radius of Earth is R) The magnitude of body's acceleration, a(r) as a function of the distance r from the Earth's center is
View Solution
