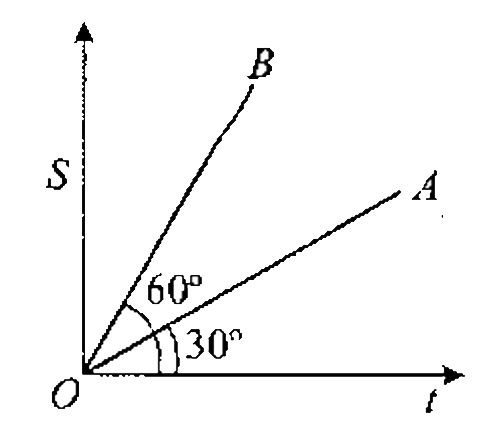
The displacement-time graph for two particles A and B are straight lines inclined at angles of 30∘ and 60∘ with the time axis. The ratio of velocities of VA:VB is
1:2
1:√3
√3:1
1:3
The correct Answer is:D
To solve the problem, we need to determine the velocities of two particles A and B based on the angles of their displacement-time graphs.
1. Understanding the Graphs:
- The displacement-time graph for particle A is inclined at an angle of 30∘ with the time axis.
- The displacement-time graph for particle B is inclined at an angle of 60∘ with the time axis.
2. Identifying the Velocity:
- The velocity of a particle can be calculated from the slope of the displacement-time graph.
- Mathematically, the velocity V is given by:
V=ΔDΔt
- In the context of the graph, this is equivalent to the slope of the line, which can be expressed in terms of the tangent of the angle of inclination.
3. Calculating Velocities:
- For particle A, the velocity VA can be expressed as:
VA=tan(30∘)
- For particle B, the velocity VB can be expressed as:
VB=tan(60∘)
4. Finding the Ratio of Velocities:
- We need to find the ratio of the velocities VA:VB:
VAVB=tan(30∘)tan(60∘)
5. Using Known Values of Tangents:
- We know that:
tan(30∘)=1√3andtan(60∘)=√3
- Substituting these values into the ratio:
VAVB=1√3√3=13
6. Final Ratio:
- Therefore, the ratio of the velocities VA:VB is:
VA:VB=1:3
Summary:
The ratio of the velocities of particles A and B is 1:3.
- The displacement-time graph for particle A is inclined at an angle of 30∘ with the time axis.
- The displacement-time graph for particle B is inclined at an angle of 60∘ with the time axis.
- The velocity of a particle can be calculated from the slope of the displacement-time graph.
- Mathematically, the velocity V is given by:
V=ΔDΔt
- In the context of the graph, this is equivalent to the slope of the line, which can be expressed in terms of the tangent of the angle of inclination.
- For particle A, the velocity VA can be expressed as:
VA=tan(30∘)
- For particle B, the velocity VB can be expressed as:
VB=tan(60∘)
- We need to find the ratio of the velocities VA:VB:
VAVB=tan(30∘)tan(60∘)
- We know that:
tan(30∘)=1√3andtan(60∘)=√3
- Substituting these values into the ratio:
VAVB=1√3√3=13
- Therefore, the ratio of the velocities VA:VB is:
VA:VB=1:3
The ratio of the velocities of particles A and B is 1:3.
Topper's Solved these Questions
- MOTION IN ONE DIMENSIONBook:ERRORLESS Chapter:MOTION IN ONE DIMENSIONExercise:Non-uniform Motion
Explore 86 Videos
- MOTION IN ONE DIMENSIONBook:ERRORLESS Chapter:MOTION IN ONE DIMENSIONExercise:Relative Motion
Explore 13 Videos
- MOTION IN ONE DIMENSIONBook:ERRORLESS Chapter:MOTION IN ONE DIMENSIONExercise:Motion In One Dimension
Explore 24 Videos
- GRAVITATIONBook:ERRORLESS Chapter:GRAVITATIONExercise:SET
Explore 27 Videos
- MOTION IN TWO DIMENSIONBook:ERRORLESS Chapter:MOTION IN TWO DIMENSIONExercise:Exercise
Explore 319 Videos
Similar Questions
A particle experiences a constant acceleration for 20 sec after starting from rest. If it travels distance S1 in the first 10 sec and a distance S2 in the next 10 sec, Then
View SolutionTwo trains, each 50m long, are travelling in opposite directions with velocities 10ms−1and15ms−1. The time of their crossing each other is.
View SolutionA particle moves along the side AB, BC, CD of a square of side 25 m with a velocity of 15ms−1Its average velocity is
View SolutionTwo identical spheres are placed in contact with each other. The force of gravitation between the spheres will be proportional to ( R = radius of each sphere)
View SolutionIf the body is moving in a circle of radius r with a constant speed v , its angular velocity is
View SolutionThe displacement time graph for two particles AandB are straight lines inclined at 30∘ with time axis and at 30∘ to displacement axis respectively. Calcualte ratio of velocities of the two particles.
View SolutionThe displacement-time graph for two particle A and B are straight lines inclined at angles of 45^(@) and 60^(@) with the time axis. The ratio of velocities of v_(A) and v_(B) is
View SolutionThe displacement time graphs of two bodies A and B are shown in figure. The ratio of velocity of A to velocity of B,vA/vB is:

View SolutionThe displacement-time graph for two particle A and B straight lines inclined at angle of 30∘ and 90∘ with the time axis. The ratio of the velocities VA and VB is :
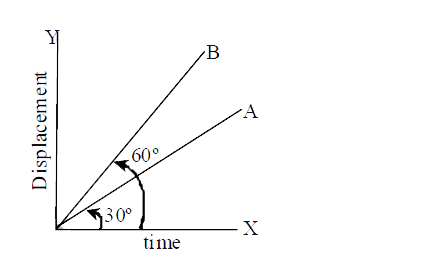
View Solutionदो कणो A तथा B के विस्थापन - समय ग्राफ सरल रेखाएँ है जो समय अक्ष से क्रमशः 30∘ तथा 60∘ के कोण बनाती है यदि कणो के वेग क्रमशः vA तथा vB हों तो VA/vB होगा :
View SolutionFrom the adjoining displacement-time graph for two particles A & B the ratio of velocitiesvA:vB will betime
View SolutionThe displacement - time graph for two particles A and B is as follows. The ratio (v_(A))/(v_(B)) is
View Solutionदो कण A और Bके समय - विस्थापन वक्र सरल रेखाएँ हैं जो समय अक्ष के साथ क्रमशः 30∘ व 60∘ कोण बनाते हैं | इनके वेगों vA:vB में अनुपात होगा
View SolutionCompletion type Question : The displacement time graphs for two particles A and B are straight lines inclined at angles of 30∘ and 45∘ with the time axis. The ratio of their velocities vA:vB = ………..
View SolutionThe displacement time graph for two particles A and B are straight lines inclined at angles 30∘and60∘ with the time axis,f he ratio of the velocities VA and VB is
View Solution

