Two rods of same length and material transfer given amount of heat in 12 s, when they are joined end to end. When they are joined parallelly then they will transfer same amount of heat in same conditions in
1.5s
3s
24s
48s
The correct Answer is:B
To solve the problem, we need to analyze the heat transfer through two rods when they are connected in series and then in parallel. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the Given Information
We have two rods of the same length and material. They transfer a given amount of heat (ΔQ) in 12 seconds when connected end to end (in series).
Step 2: Define Thermal Resistance
The thermal resistance (R) of a rod can be defined as:
R=LkA
where:
- L = length of the rod
- k = thermal conductivity of the material
- A = cross-sectional area of the rod
Since both rods are of the same length and material, their thermal resistance will be the same, say R.
Step 3: Calculate Equivalent Resistance in Series
When the rods are connected in series, the total thermal resistance Req1 is:
Req1=R+R=2R
Step 4: Calculate Equivalent Resistance in Parallel
When the rods are connected in parallel, the total thermal resistance Req2 is given by:
1Req2=1R+1R
This simplifies to:
1Req2=2R
Thus,
Req2=R2
Step 5: Relate Time to Thermal Resistance
The time taken to transfer the same amount of heat (ΔQ) is directly proportional to the thermal resistance:
Δt∝R
This means:
Δt1Δt2=Req1Req2
Step 6: Substitute the Values
From our earlier calculations:
- Δt1=12 seconds (time in series)
- Req1=2R
- Req2=R2
Substituting these values into the equation gives:
12Δt2=2RR2
Step 7: Simplify the Equation
This simplifies to:
12Δt2=4
Step 8: Solve for Δt2
Now, solving for Δt2:
Δt2=124=3 seconds
Conclusion
Thus, when the rods are connected in parallel, they will transfer the same amount of heat in 3 seconds.
We have two rods of the same length and material. They transfer a given amount of heat (ΔQ) in 12 seconds when connected end to end (in series).
The thermal resistance (R) of a rod can be defined as:
R=LkA
where:
- L = length of the rod
- k = thermal conductivity of the material
- A = cross-sectional area of the rod
When the rods are connected in series, the total thermal resistance Req1 is:
Req1=R+R=2R
When the rods are connected in parallel, the total thermal resistance Req2 is given by:
1Req2=1R+1R
This simplifies to:
1Req2=2R
Thus,
Req2=R2
The time taken to transfer the same amount of heat (ΔQ) is directly proportional to the thermal resistance:
Δt∝R
This means:
Δt1Δt2=Req1Req2
From our earlier calculations:
- Δt1=12 seconds (time in series)
- Req1=2R
- Req2=R2
12Δt2=2RR2
This simplifies to:
12Δt2=4
Now, solving for Δt2:
Δt2=124=3 seconds
Thus, when the rods are connected in parallel, they will transfer the same amount of heat in 3 seconds.
Topper's Solved these Questions
Similar Questions
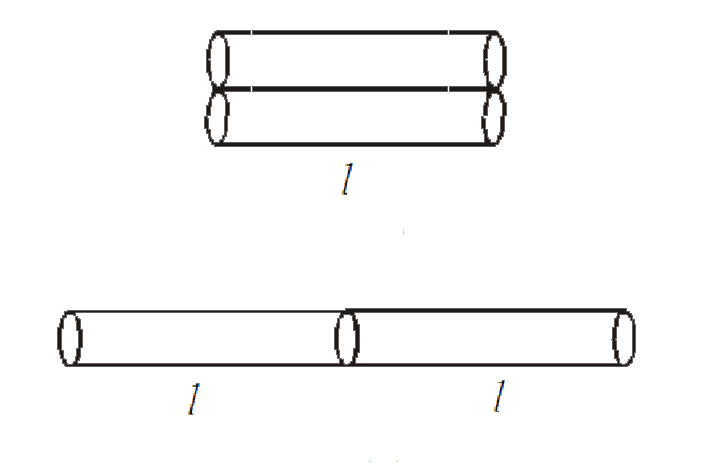
Two rods of same length and transfer a given amount of heat 12 second, when they are joined as shown in figure (i). But when they are joined as shwon in figure (ii), then they will transfer same heat in same conditions in
View SolutionThere are two sphers of same radius and material at the same temperature but one being solid while the other hollow. Which sphere will expand more if they are given the same amount of heat ?
View Solution
Knowledge Check
Two rods of the same length and material transfer a given amount of heat in 12 seconds when they are joined end to end. But when they are joined lengthwise, they will transfer the same amount of heat, in the same conduction, in :
A24 sB10 sC15 sD48 sTwo rods are of same material and having same length and area. If heat ΔQ flows through them for 12 min when they are joined side by side. If now both the rods are joined in parallel, then the same amount of heat ΔQ will flow in
A24 minB3 minC12 minD6 minTwo rods made of same material having same length and diameter are joined in series. The thermal power dissipated through then is 2W.If they are joined in parallel, the thermal power dissipated under the same conditions on the two ends of the rods, will be :
A16 WB8 WC4 WD2 W
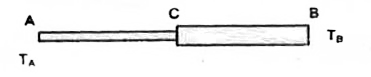
Two rods of same length and same material having area of cross section A and 4A respectively are joined as shown in the figure. If TA and TB are temperatures of free ends in steady state. The temperature of junction point C is (Assume no heat loss wil take place through lateral surface)
View SolutionThe lengths and radii of two rods made of same material are in the ratios 1 : 2 and 2 : 3 respectively. If the temperature difference between the ends for the two rods be the same, then in the steady state, the amount of heat flowing per second through them will be in the ratio
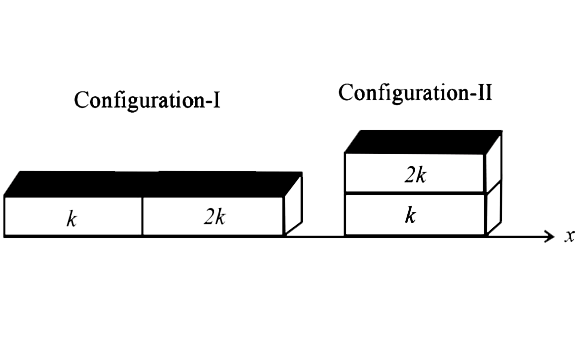
View SolutionTwo rectangular blocks, having identical dimensions, an be arranged either in configuration-I or in configuration-II as shown in the figure. One of the blocks has thermal conductivity k and the other 2k. The temperature difference between the ends along the x-axis is the same in both the configurations. It takes 9s to transport a certain amount of heat from the hot end to the cold end in the configuration-I. The time to transport the same amount of heat in the configuration-II is
View SolutionTwo rods of the same length and areas of cross-section A1 and A2 have their ends at the same temperature. K1 and K2 are the thermal conductivities of the two rods. The rate of flow of heat is same in both the rods if-
View SolutionThe lengths and radii of two rods made of same material are in the ratios 1 : 2 and 2 : 3 respectively. If the temperature difference between the ends for the two rods be the same, then in the steady state, the amount of heat flowing per second through them will be in the ratio
View Solution

