In given circuit initially switch S1 is closed for long time and then opened and now S2 is closed. The total energy dissipated in 4Ω resistor is equal to :-
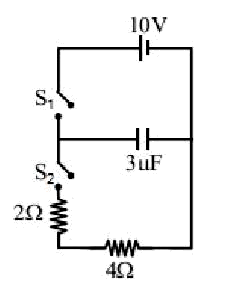
0.5 mJ
0.05 mJ
0.1 mJ
10 mJ
The correct Answer is:C
H1+H2=12CV2
H1H2=R1R2=24=12
H1=H22
H22+H2=12CV2
H2=13CV2
=13×3×10−6×(10)2=10_4J
=0.1mJ
Topper's Solved these Questions
Similar Questions
Initally switch S1 is closed, after a long time, S1 is opened and S2 is closed. Find the heat produced in coil after long time.
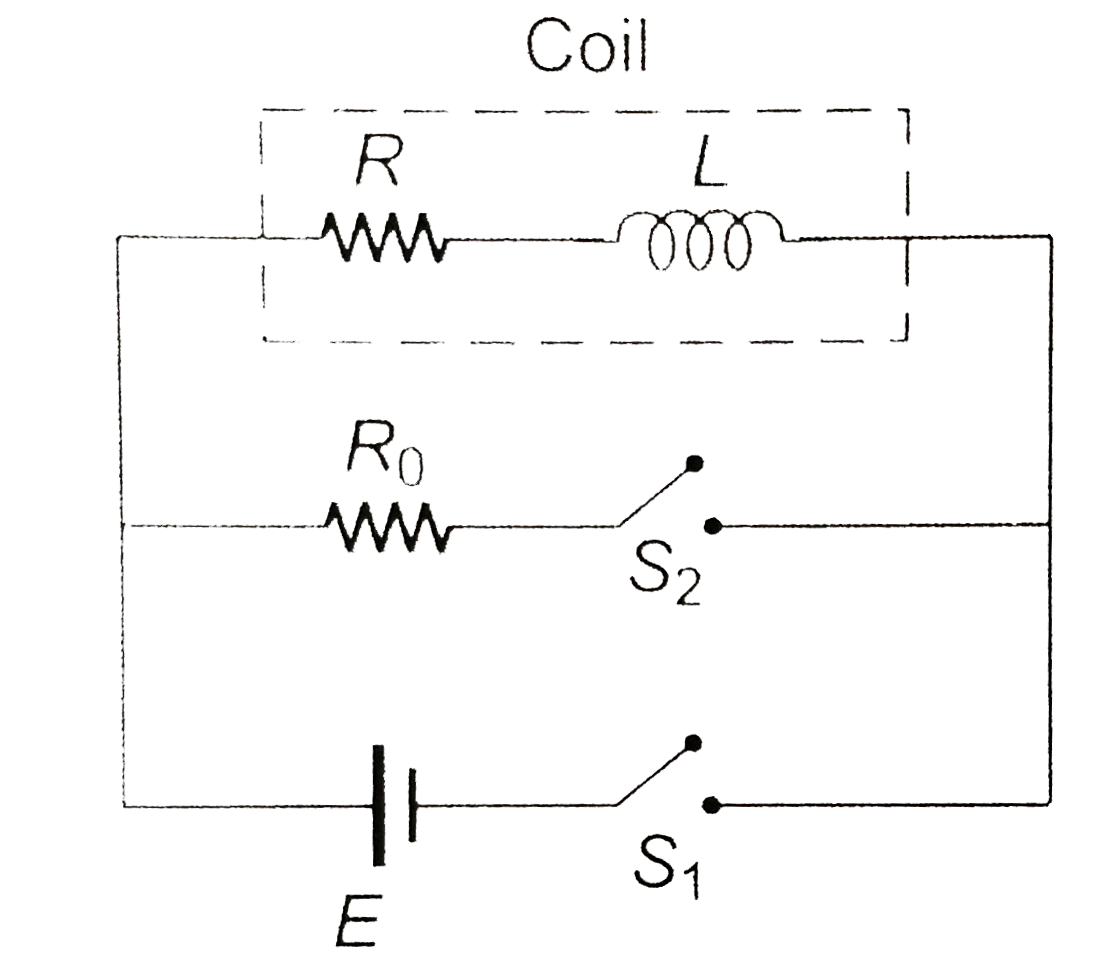
View SolutionIn given circuit initially switch Sw1 is closed and Sw2 is open, Now Sw1 is opened and Sw2 is closed, what is the heat liberated in resistance R?

View Solution
Knowledge Check

In given LR circuit the switch S is closed at time t=0 thenAThe ratio of induced emfs in the inductors of inductance L and 2L will be constantBThe ratio of induced emfs in the inductor of inductance L and 2L will be time varyingCthe potential difference VA−VB increases with timeDThe potential difference VA−VB will be constantIn Fig. switch S is closed for a long time. At t=0, if it is opened, then
 Atotal heat produced in resistor R after opening the switch is 12LεR2Btotal heat produced in resistor R1 after opening the switch is 12Lε2R2(R1R1+R2)Cheat produced in resistor R1 after opening the switch is 12R2Lε2(R1+R2)R2Dno heat will be produced in R1
Atotal heat produced in resistor R after opening the switch is 12LεR2Btotal heat produced in resistor R1 after opening the switch is 12Lε2R2(R1R1+R2)Cheat produced in resistor R1 after opening the switch is 12R2Lε2(R1+R2)R2Dno heat will be produced in R1The switch S shown in figure is kept closed for a long time and then opened at t = 0, then the current in the middle 20Ω resistor at t=0.25 ms is :
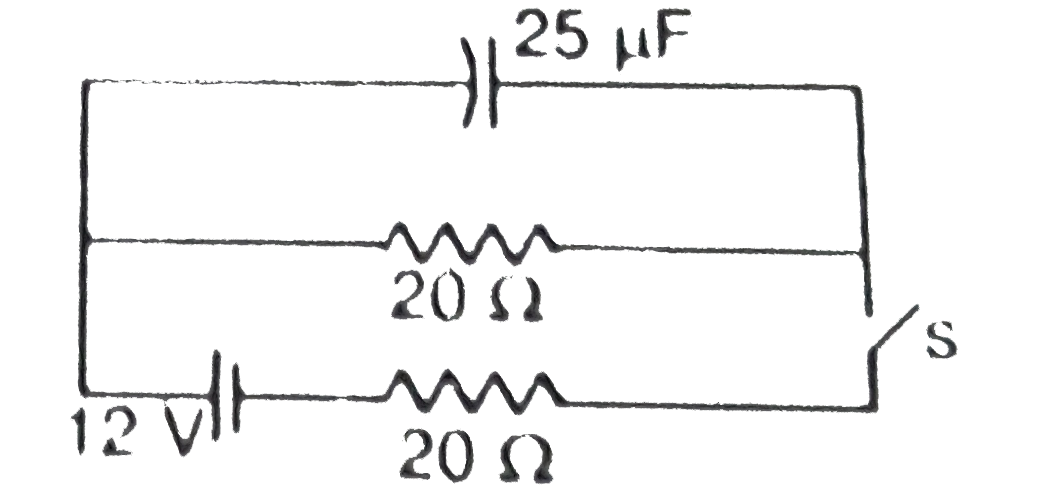 A0.629AB0.489AC0.189AD23 mA
A0.629AB0.489AC0.189AD23 mA
At any time S1 switch is opened and S2 is closed then find out heat generated in circuit.
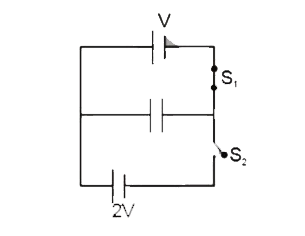
View SolutionAt any time S1 switch is opened and S2 is closed then find out heat generated in circuit.
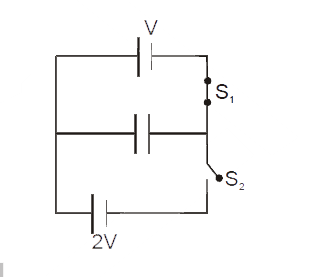
View SolutionIn the given circuit S1 and S2
are switches. S2 is closed for
a long time and S1 remains
Open. Now S1 is also closed. Here
R=10Ω,L=1 mH and
ε=3V.Letdidt is the
magnitude of rate of change of
current (in"A/s"). Just after S1
is Closed. The value for the
inductor L is
didt=x×103A/s. Then find x.
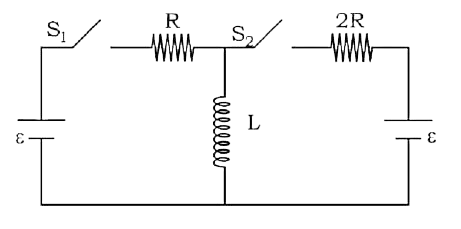
View SolutionA capacitor of capacitance 3μF is first charged by connecting it across a 10V battery by closing key K1, then it is allowed to get discharged through 2Ω and 4Ω resistors by opening K1 and closing the key K2. The total energy dissipated in the 2Ω resistor is equal to

View SolutionA capacitor of capacitance 3μF is first charged by connecting it across a 10 V battery by closing key K1. Then it is allowed to get discharged through 2Ω and 4Ω resistors by closing the key K2. The total energy dissipated in the 4Ω resistor is equal to

View Solution

