The instant of time at which acceleration and velocity are perpendicular is :-

0.6 sec
1.2 sec
2.4 sec
None of this
The correct Answer is:B
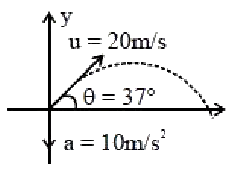
The question can be reframed as shown in figure. The path of particle is parabolic.
∴→a⊥→v ar maximum height, that is at half time of flight.
Hence t0=usinθa=20×3/510=1.2 sec.
Topper's Solved these Questions
Similar Questions
A foot ball is thrown in a parabolic path. Is there a point at which the acceleration is parallel to the velocity ?Perpendicular to the velocity ? Explain.
View SolutionGive examples where a. the velocity of a particle is zero buts its acceleration is not zero. b.the velocity is opposite in direction to the acceleration, c. the velocity is perpendicular to the acceleration.
View Solution
Knowledge Check
At what point of a projectile motion acceleration and velocity are perpendicular to each other
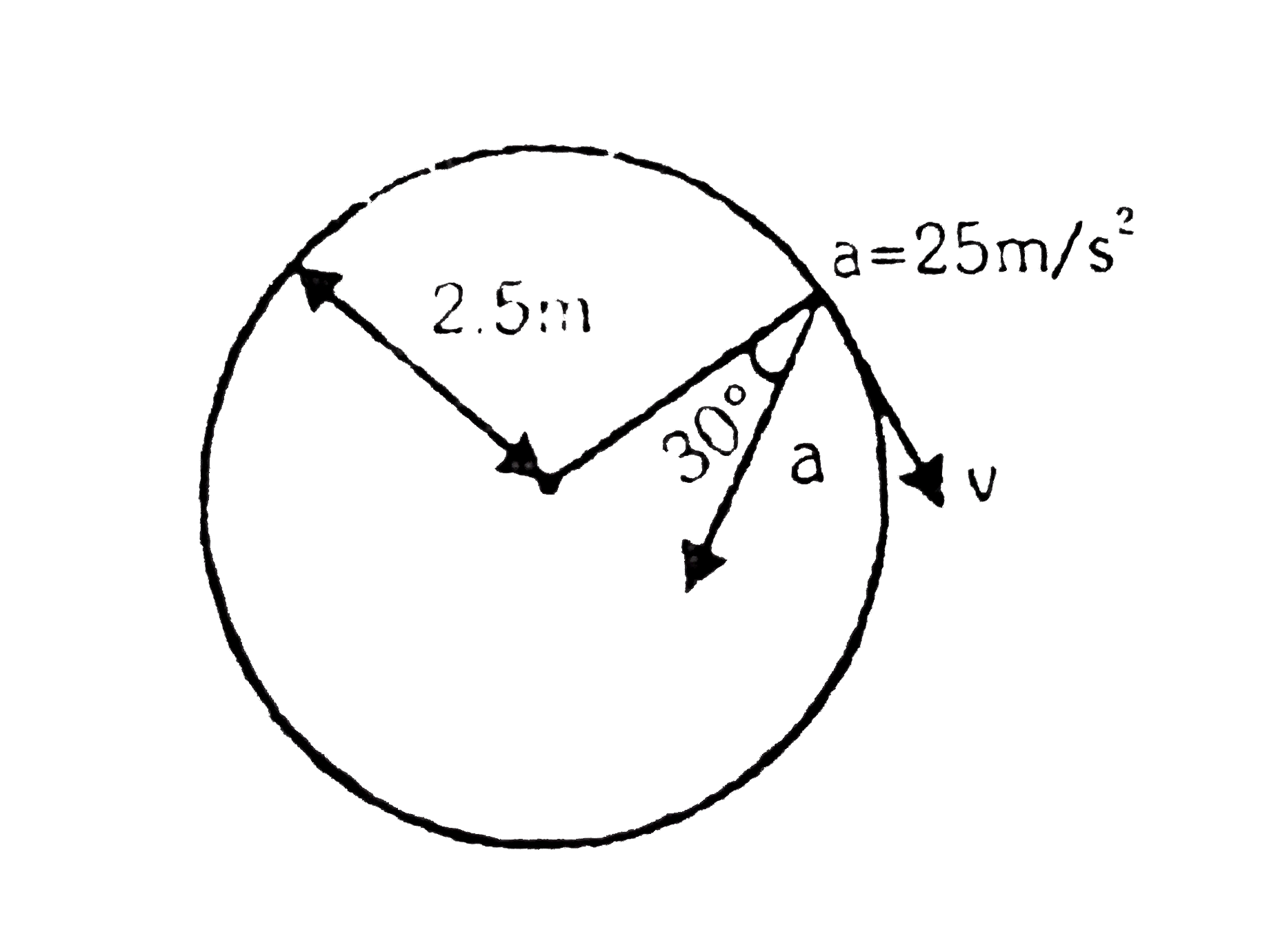
AAt the point of projectionBAt the point of dropCAt the topmost pointDAny where in between the point of projection and topmost pointFigure shows the direction of the total acceleration and velocity of a particle moving clockwise in a circle radius m at an instant of time. Tangential acceleration this instant is 5m/s2. Which of the following statements is not correct?
 AThe centripetal aceleration is 5√3ms−2BParticle is speeding up.CThe net acceleration is 10ms−2DThe particle is slowing down.
AThe centripetal aceleration is 5√3ms−2BParticle is speeding up.CThe net acceleration is 10ms−2DThe particle is slowing down.For any particle moving with some velocity (→v) & acceleration (→a), tangential acceleration & normal acceleration are defined as follows.
Tangential acceleration - The component of acceleration in the direction of velocity.
Normal acceleration - The component of acceleration in the direction perpendicular to velocity.
If at a given instant, velocity & acceleration of a particle are given by .
→c=4ˆi+3ˆj
vaca=10ˆi+15ˆj+20ˆk
Find the tangential acceleration of the particle at the given instant :-A17(4ˆi+3ˆj)B175(4ˆi+3ˆj)C17(4ˆi−3ˆj)D175(4ˆi−3ˆj)
Suppose velocity of a cricket ball hit by a batsman is given by
→v=(2ˆi+6ˆj+(∘0−10t)ˆk)m/s
Find the time (t) the acceleration of the ball is perpendicular to its velocity.
View SolutionFigur shows the total acceleration and velocity of a particle moving clockwise in a circle of radius 2.5m at a given instant of time. At this instant, find:
(a) the radius acceleration,
(b) the speed of the acceleration,
(c) its tangential acceleration.

View SolutionFigure shows the total acceleration and velocity of a particle moving clockwise in a circle of radius 2.5 m at a given instant of time. At this instant, Find: (i) the radial acceleration, (ii) the speed of the particle and (iii) its tangential acceleration.
View SolutionDerive the relation between acceleration, change in velocity and time.
View SolutionFor any particle moving with some velocity (→v) & acceleration (→a), tangential acceleration & normal acceleration are defined as follows.
Tangential acceleration - The component of acceleration in the direction of velocity.
Normal acceleration - The component of acceleration in the direction perpendicular to velocity.
If at a given instant, velocity & acceleration of a particle are given by .
→c=4ˆi+3ˆj
→a=10ˆi+15ˆj+20ˆk
Find the normal acceleration of the particles at the given instant :-
View Solution

