m संहति के पत्थर को किसी डोरी के एक सिरे से बांधकर R त्रिज्या के ऊर्ध्वाधर वृत्त में घुमाया जाता है । वृत्त के निम्नतम तथा उच्चतम बिन्दुओ पर उर्ध्वाधरतः अधोमुखी दिशा में नेट बल है - (सही विकल्प चुनिए)
यहाँ तथा निम्नतम बिंदु पर तनाव तथा चाल दर्शाते है तथा इनके उच्चतम बिंदु पर तदनुरूपी मान है ।
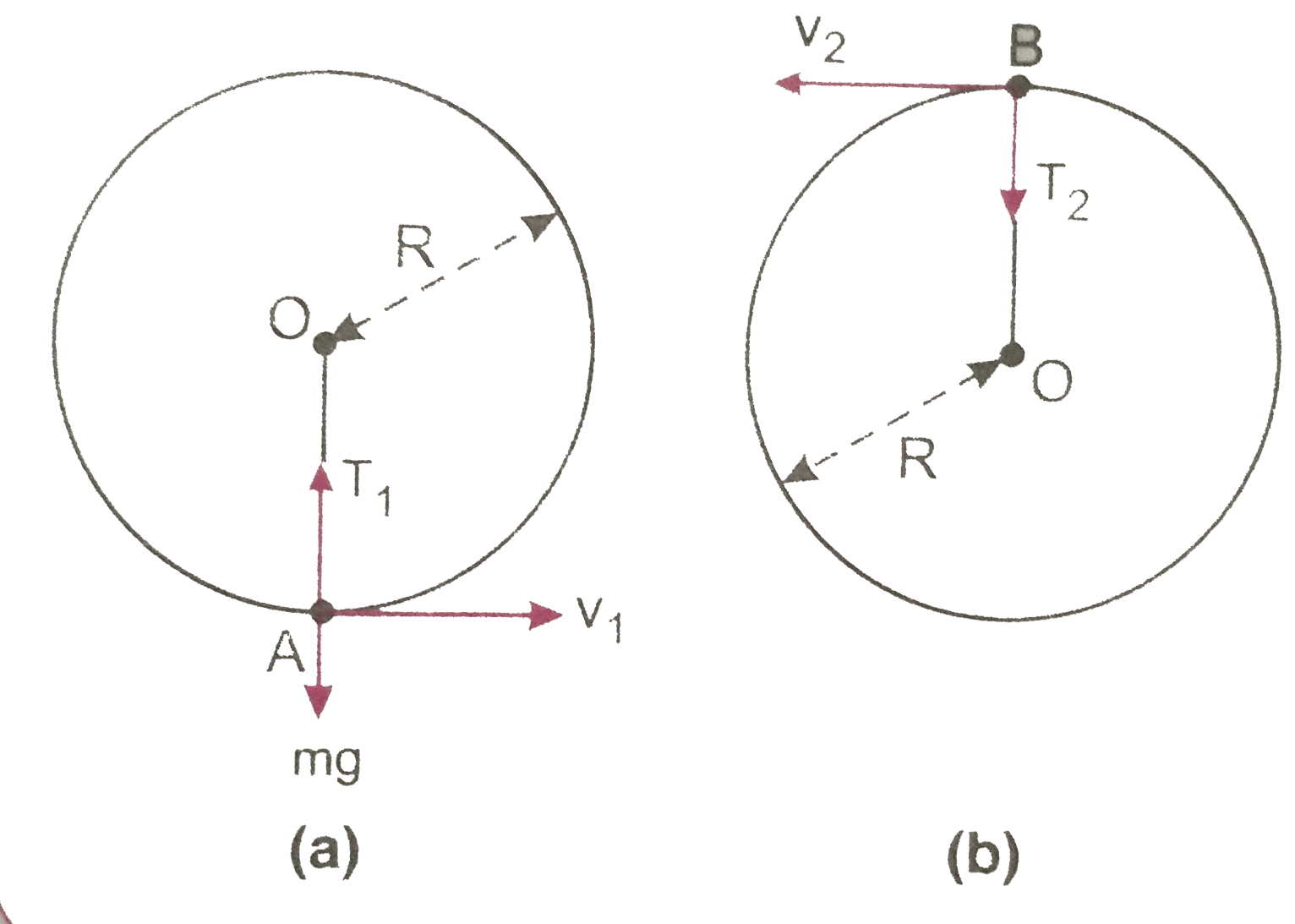
निम्नतम बिंदु पर, इस स्थिति में, पत्थर पर निम्नलिखित दो बल लगेंगे | [चित्र 6.29 (a)]
(i) पत्थर का भार mg नीचे की ओर,
(ii) डोरी में तनाव , वृत्तीय पथ केन्द्र की ओर (अर्थात ऊपर की ओर) । इस प्रकार पत्थर की वृत्तीय गति को बनाए रखने के लिए आवश्यक अभिकेंद्रीय बल, वृत्तीय पथ के केंद्र की ओर लग रहे परिणामी बल द्वारा प्राप्त हो जाता है ।
उच्चतम बिंदु पर, इस स्थिति में, पत्थर पर निम्नलिखित दो बल लगेंगे [चित्र 6.29 (b)],
(i) पत्थर का भार mg नीचे की ओर,
(ii) डोरी में तनाव , वृत्तीय पथ के केंद्र की ओर (अर्थात नीचे की और) ।
इस प्रकार पत्थर की वृत्तीय गति को बनाए रखने के लिए आवश्यक अभिकेंद्रीय बल, वृत्तीय पथ के केन्द्र की और लग रहे परिणामी बल द्वारा प्राप्त हो जाता है
अतः सही विकल्प (i) है
Topper's Solved these Questions
- वृत्तीय गति Book:SHIVLAAL PUBLICATIONChapter:वृत्तीय गति Exercise:बोधात्मक प्रश्न
Explore 8 Videos
- वृत्तीय गति Book:SHIVLAAL PUBLICATIONChapter:वृत्तीय गति Exercise:आंकिक प्रश्न
Explore 2 Videos
- वृत्तीय गति Book:SHIVLAAL PUBLICATIONChapter:वृत्तीय गति Exercise:संख्यात्मक प्रश्न (ऊर्ध्वाधर वृत्त में गति)
Explore 2 Videos
- मापन एवं मात्रक Book:SHIVLAAL PUBLICATIONChapter:मापन एवं मात्रक Exercise:वस्तुनिष्ठ प्रश्न
Explore 67 Videos
- समतल में गति Book:SHIVLAAL PUBLICATIONChapter:समतल में गति Exercise:वस्तुनिष्ठ प्रश्न
Explore 58 Videos
Similar Questions
चक्र दोले में बैठा बालक अपनी कुर्सी की भुजाओ को बाहर की ओर धकेलता है क्यों ?
View Solutionएक वायुयान नियत चाल 900 किमी/घण्टा से उड़ता हुआ त्रिज्या 1 किमी का क्षैतिज वृत्त बनाता है । इसके अभिकेन्द्री त्वरण की गुरुत्वीय त्वरण से तुलना कीजिए ।
View Solutionएक वृत्तीय मार्ग की त्रिज्या 1600 मीटर तथा पटरियों के बीच की दूरी 1⋅4 मीटर है । यदि रेलगाड़ी चाल 60 किमी/घण्टा से सुरक्षित गुजरती है तो बाहर की पटरी, अंदर की पटरी की अपेक्षा कितनी ऊँची है ? (g=10 मीटर/सेकण्ड2)
View SolutionS.I. पद्धति में कुल मूल मात्रको की संख्या है :
View Solutionनिम्नलिखित में से अदिश राशि है :
View SolutionIf the normals at points t1andt2 meet on the parabola, then t1t2=1 (b) t2=−t1−2t1 t1t2=2 (d) none of these
View SolutionA stone of mass m tied to one end of a string is revolved in a vertical circle of radius R the net forces at the lowest (FL and highest (FH) points of the circle directed vertically downwards are :
(a) FL=mg−T1FH=mg+T2
(b) FL=mg+T1,FH=mg−T2
(c) FL=mg+T1−mυ21R,FH=mg−T2+mυ21R
(d) FL=mg−T1−mυ21R,FH=mg+T2+mυ12R
Choose corret alternative T1,υ1 denote the tension and speed at the lowest point T2,υ2 denote corresponding valuse at the highest point .
View SolutionFor any arbitrary motion in space, which of the following relations are true?
(a) vaverage=(1/2)(v(t1)+v(t2))
(b) vaverage=[r(t2)−r(t1]/(t2−t1)
(c) v(t)=v(0)+at
(d) aaverage=[v(t2)−v(t1)]/(t2−t1)
The average stands for average of the quantity over time interval t1 to t2
View Solutionm संहति के पत्थर को किसी डोरी के एक सिरे से बांधकर R त्रिज्या के ऊध्वार्धर वृत्त में घुमाया जाता है। वृत्त के निम्नतम तथा उच्तम बिन्दुओ पर ऊर्ध्वधरत: अधोमुखी दिशा में नेट बल है: (सही विकल्प चुनिए)
निम्नतम बिंदु पर उच्चतम बिंदु पर
(i)mg−T1mg+T2(ii)mg+T1mg−T2(iii)mg+T1(mv21)/Rmg−T2+(mv22)/R(iv)mg−T1−(mv21)/Rmg+T2+(mv22)/R
यहाँ T1 तथा v1 निम्नतम बिंदु पर तनाव तथा चाल दर्शाते है। T2 तहत v2 इनके उच्चतम बिंदु पर तदनुरूपी मान है।
View Solutionदर्शाइए कि परवलय y2=4ax पर बिंदुओं t1,t2 और t3 से बने त्रिभुज के क्षेत्रफल का परिमाण a2(t1−t2)(t2−t3)(t3−t1) है।
View SolutionA stone of mass m tied to the end of a string revolves in a vertical circle of radius R. The net force at the lowest and highest points of the circle directed vertically downwards are: [ Choose the correct alternative]
Lowest Point Highest point
(a) mg +T1 mg+T2
(b) mg +T1 mg−T2
(c ) mg + T1−(mv21)/R mg−T2+(mv21)/R (d) mg -T1−(mv21)/R mg+T2+(mv21)/R
T1andv1 denote the tension and speed at the lowest point. T2andv2 denote corresponding values at the highest point.
View SolutionFor any arbitrary motion in space , which of the following relations are true : (a) Vaverage=(1/2)(v(t1)+v(t2))
(b) Vaverage=[r(t2)−r(t1)]/(t2−t1)
(c ) V(t)=V(0)+at
(d) r(t)=r(0)+v(0)T+(1/2)at2
(e ) aaverage=[v(t2)−v(t1)]/(t2−t1)
(The average stands for average of the quantity over the time interval t1 to t2)
View SolutionFor any arbitrary motion in space , which of the following relations are true : (a) V_("average")=(1//2)(v(t_(1))+v(t_(2))) (b) V_("average")=[r(t_(2))-r(t_(1))]//(t_(2)-t_(1)) (c ) V(t)=V(0)+at (d) r(t) =r(0)+v(0)T+(1//2)at^(2) (e ) a_("average")=[v(t_(2))-v(t_(1))]//(t_(2)-t_(1)) (The average stands for average of the quantity over the time interval t_(1)" to "t_(2))
View SolutionFor any arbitrary motion in space , which of the following relations are true : (a) Vaverage=(1/2)(v(t1)+v(t2))
(b) Vaverage=[r(t2)−r(t1)]/(t2−t1)
(c ) V(t)=V(0)+at
(d) r(t)=r(0)+v(0)T+(1/2)at2
(e ) aaverage=[v(t2)−v(t1)]/(t2−t1)
(The average stands for average of the quantity over the time interval t1 to t2)
View SolutionFollowing are four different relation about displacement,velocity and acceleration for the motion of a particle in general.Choose the incorrect one (S). a) V_(av)=(1)/(2)[v(t_(1))+v(t_(2))] b) V_(av)=(r(t_(2))-r(t_(2)))/(t_(2)-t_(1)) c)r= (1)/(2)(v(t_(2))-v(t_(1))(t_(2)-t_(1)) d) a_(av)=(v(t_(2))-v(t_(1)))/(t_(2)-t_(1))
View Solution