A stone of mass m tied to one end of a string is revolved in a vertical circle of radius R the net forces at the lowest $(F_{L}$ and highest $(F_{H})$ points of the circle directed vertically downwards are :
(a) $F_{L} = m g - T_{1} F_{H} = m g + T_{2}$
(b) $F_{L} = m g + T_{1}, F_{H} = m g - T_{2}$
(c) $F_{L} = m g + T_{1} - \frac{m υ_{1}^{2}}{R}, F_{H} = m g - T_{2} + \frac{m υ_{1}^{2}}{R}$
(d) $F_{L} = m g - T_{1} - \frac{m υ_{1}^{2}}{R}, F_{H} = m g + T_{2} + \frac{m υ_{2}^{1}}{R}$
Choose corret alternative $T_{1}, υ_{1}$ denote the tension and speed at the lowest point $T_{2}, υ_{2}$ denote corresponding valuse at the highest point .

Video Solution

Text Solution

Verified by Experts

The net force at the lowest point L is $F_{L} = (m g - T_{1}$ and the net force at the highest point H is $F_{H = m g + T_{2}}$ Thereforce alternative (a) is correct For details.

Updated on:21/07/2023

Class 11 PHYSICS NEWTONS LAW OF MOTION

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
A main revolves a stone of mass $m$ tied to the end of a string in a circle of radius R The net force at the lowest and height point of the circle directed vertical downward are
Here $T_{1}, T_{2}$ and $(v_{1}, v_{2})$ denote the tension in the string (and the speed of the stone) at the lowest and highest points, respectively.
A $\begin{matrix} Lowest point & highest point m g - T_{1} & m g + T_{2} \end{matrix}$
B $\begin{matrix} Lowest point & highest point m g + T_{1} & m g - T_{2} \end{matrix}$
C $\begin{matrix} Lowest point & highest point m g + T_{1} - \frac{m v^{2}}{r} & m g - T_{2} + \frac{m v^{2}}{r} \end{matrix}$
D $\begin{matrix} Lowest point & highest point m g - T_{1} - \frac{m_{1} v_{1}^{2}}{R} & m g + T + \frac{m_{1} v_{1}^{2}}{R} \end{matrix}$
Question 2 - Select One
A stone of mass m tied to the end of a string revolves in a vertical circle of radius R. The net forces at the lowest and highest points of the circle directed vertically downwards are: [Choose the correct alternative] Lowest point Highest point
$T_{1}$ and $V_{1}$ denote the tension and speed at the lowest point $T_{2}$ and $V_{2}$ denote the corresponding values at the highest points.
A $m g - T_{1} m g + T_{2}$
B $m g + T_{1} m g - T_{2}$
C $m g + T_{1} - (m v_{1}^{2}) / R m g - T + (m v_{1}^{2}) / R$
D $m g - T_{1} - (m v_{1}^{2}) / R m g + t_{2} + (m v_{1}^{2}) / R$
Question 3 - Select One
An object of mass $m$ is tied to a string of length $l$ and a variable force F is applied on it which brings the string gradually at angle $θ$ with the vertical. Find the work done by the force $F$ .
.
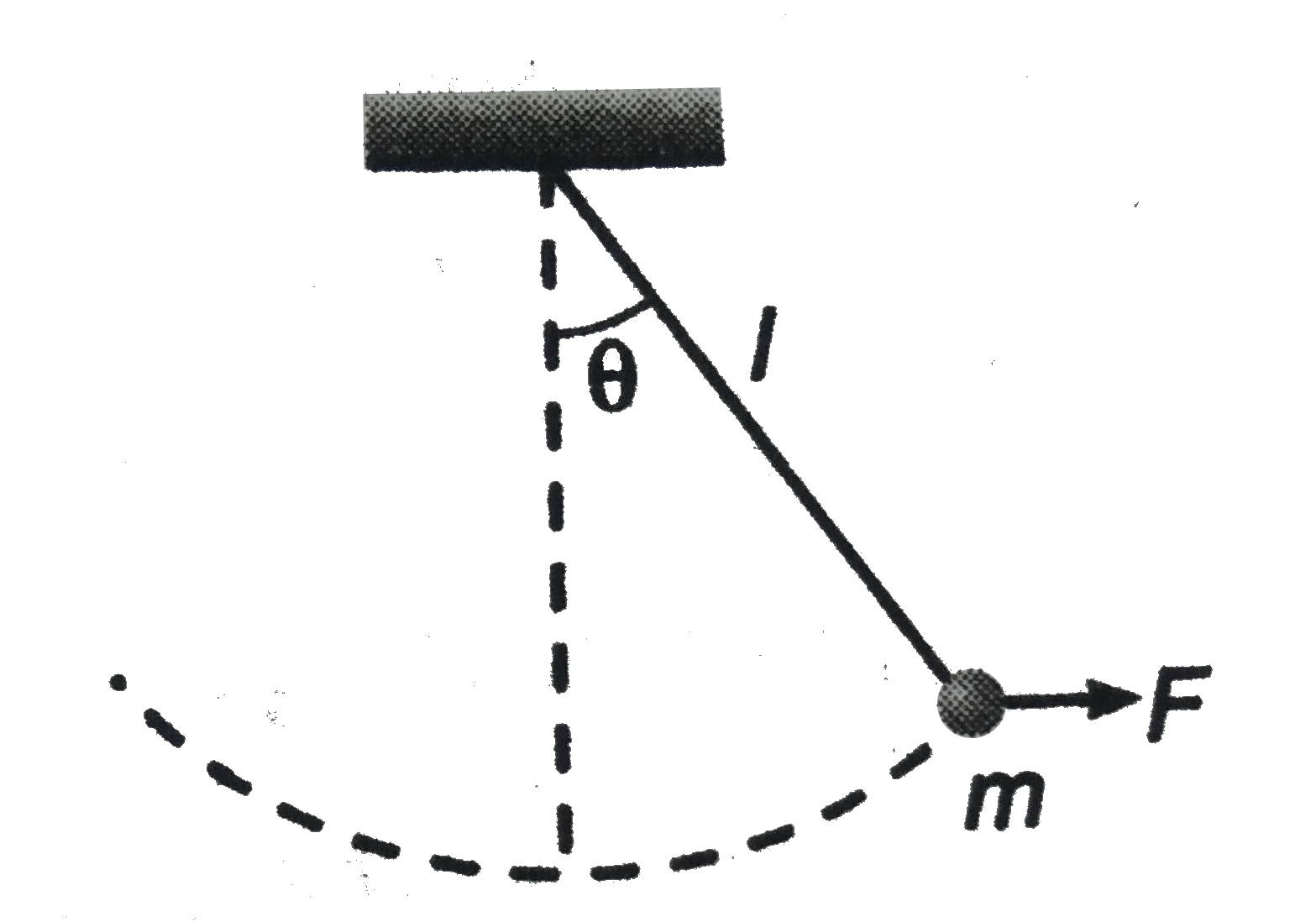A $m g l (1 + cos θ)$
B $\frac{m g}{l (1 - cos θ)}$
C $m g l (1 - cos θ)$
D $\frac{m g}{l (1 + cos θ)}$

PRADEEP-LAWS OF MOTION-EXERCISES

Home
Ask Doubt
Profile

The net force at the lowest point L is FL=(mg−T1 and the net force at the highest point H is FH=mg+T2 Thereforce alternative (a) is correct For details.

Topper's Solved these Questions

Similar Questions

Knowledge Check

An object of mass m is tied to a string of length l and a variable force F is applied on it which brings the string gradually at angle θ with the vertical. Find the work done by the force F. .

PRADEEP-LAWS OF MOTION-EXERCISES

The net force at the lowest point L is $F_{L} = (m g - T_{1}$ and the net force at the highest point H is $F_{H = m g + T_{2}}$ Thereforce alternative (a) is correct For details.

An object of mass $m$ is tied to a string of length $l$ and a variable force F is applied on it which brings the string gradually at angle $θ$ with the vertical. Find the work done by the force $F$ .
.