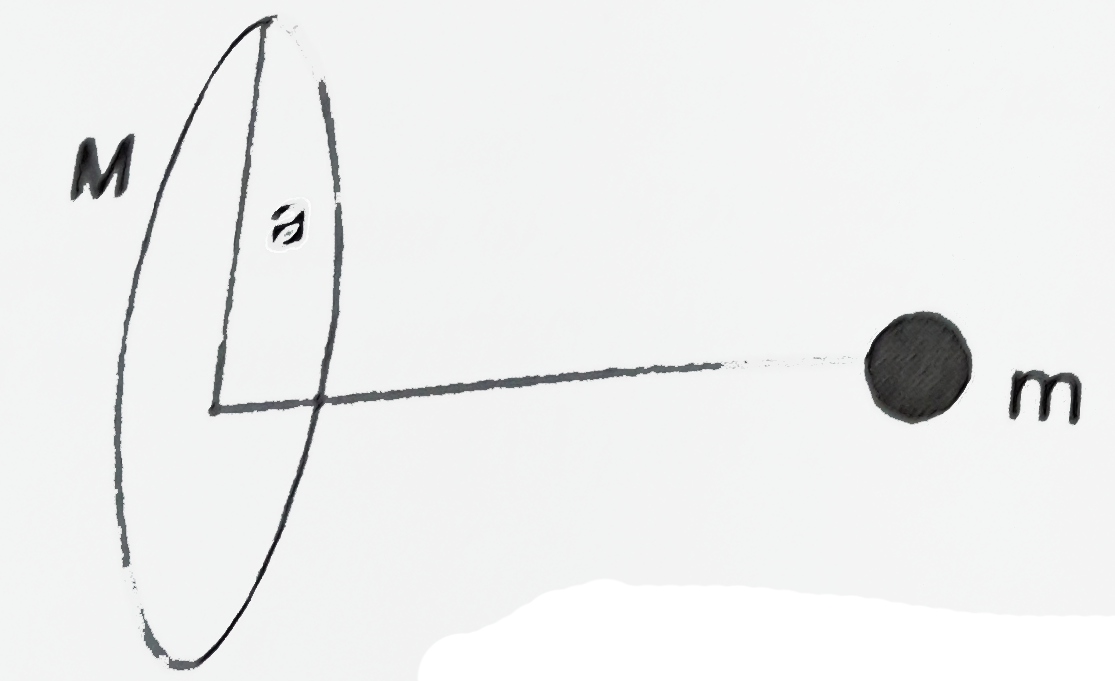
A point $P$ lies on the axis of a fixed ring of mass $M$ and radius $a$ , at a distance $a$ from its centre $C$ . A small particle starts from $P$ and reaches $C$ under gravitational attraction only. Its speed at $C$ will be.

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $\sqrt{\frac{2 G M}{a} (1 - \frac{1}{\sqrt{2}})}$

Potential at the axis of ring $V_{p} = - \frac{G M}{\sqrt{R^{2} + x^{2}}}$
$V_{p} = - \frac{G M}{\sqrt{a^{2} + a^{2}}} \Rightarrow V_{p} = - \frac{G M}{\sqrt{2} a} \Rightarrow V_{0} = - \frac{G M}{a}$
From energy conservation Loss of potential of particle = Gain of kinetic energy.
$U_{i} - U_{f} = K_{f} - K_{i}$
$- \frac{G M m}{\sqrt{2} a} - (- \frac{G M m}{a}) - \frac{1}{2} m v^{2} \Rightarrow \frac{G M}{a} (1 - \frac{1}{\sqrt{2}}) = \frac{v^{2}}{2}$
$v^{2} = \frac{2 G M}{a} (1 - \frac{1}{\sqrt{2}}) \Rightarrow v = \sqrt{\frac{2 G M}{a} (1 - \frac{1}{\sqrt{2}})}$

|

Updated on:21/07/2023

Class 11 PHYSICS GRAVITATION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A point $P$ lies on the axis of a fixed ring of mass $M$ and radius $R$ , at a distance $2 R$ from its centre $O$ . A small particle starts from $P$ and reaches $O$ under gravitational attraction only. Its speed at $O$ will be
A $\sqrt{\frac{2 G M}{R} (1 - \frac{1}{\sqrt{5}})}$
B $\sqrt{\frac{2 G M}{R}}$
C $\sqrt{\frac{2 G M}{R} (\sqrt{5} - 1)}$
Dzero
Question 2 - Select One
A point P $(R \sqrt{3} m, 0,)$ lies on the axis of a ring of mass M and radius R. The ring is located in $y - z$ plane with its centre at origin. A small particle of mass m start from P and reaches O under gravitational attraction only. Its speed at O will be.
A $\sqrt{\frac{G M}{R}}$
B $\sqrt{\frac{G m}{R}}$
C $\sqrt{\frac{G M}{\sqrt{2} R}}$
D $\sqrt{\frac{G m}{\sqrt{2} R}}$
Question 3 - Select One
A point $P (R \sqrt{3}, 0, 0)$ lies on the axis of a ring of mass M and radius R. The ring is located in yx-plane with its centre at origin O. A small particle of mass $m$ starts from P and reaches O under gravitational attraction only. Its speed at O will be
A $\sqrt{\frac{G M}{R}}$
B $\sqrt{\frac{G m}{R}}$
C $\sqrt{\frac{G M}{2 R}}$
D $\sqrt{\frac{2 m}{\sqrt{2} R}}$

BANSAL-GRAVITATION-EXERCISE -3 [Miscellaneous Exercise]

Home
Ask Doubt
Profile