Two bodies of same mass tied with an inelastic string of length l lie together. One of them is projected vertically upwards with velocity √6gl. Find the maximum height up to which the centre of mass system of the two masses rises.
The correct Answer is:l
To solve the problem, we will follow these steps:
Step 1: Understand the System
We have two bodies of the same mass m connected by an inelastic string of length l. One body (let's call it A) is projected upwards with an initial velocity of v0=√6gl, while the other body (B) remains stationary initially.
Step 2: Determine the Initial Conditions
The initial position of the center of mass (CM) of the system can be calculated as:
hCM, initial=hA+hB2=0+l22=l4
where hA=0 (the height of A) and hB=l2 (the height of B).
Step 3: Analyze the Motion of Body A
As body A moves upwards, it will continue to rise until the string becomes taut. We need to find the velocity of body B when the string becomes taut.
Step 4: Apply Conservation of Momentum
When the string becomes taut, both bodies will have the same speed v′. By conservation of momentum:
mv0+m⋅0=mv′+mv′
This simplifies to:
v0=2v′
Thus, we find:
v′=v02=√6gl2=√62√gl
Step 5: Calculate the Maximum Height of the Center of Mass
The center of mass will rise with the velocity v′ until both bodies reach their maximum height. The maximum height can be calculated using the kinematic equation:
v2=u2+2as
where v=0 (final velocity at maximum height), u=v′, and a=−g (acceleration due to gravity).
Setting up the equation:
0=(√62√gl)2−2gh
This gives:
0=64gl−2gh
Rearranging gives:
2gh=64gl
h=6l8=3l4
Step 6: Calculate the Final Height of the Center of Mass
The final height of the center of mass is the initial height of the center of mass plus the height it rises:
hCM, final=hCM, initial+h=l4+3l4=l
Final Answer
The maximum height up to which the center of mass of the system rises is:
l
---
We have two bodies of the same mass m connected by an inelastic string of length l. One body (let's call it A) is projected upwards with an initial velocity of v0=√6gl, while the other body (B) remains stationary initially.
The initial position of the center of mass (CM) of the system can be calculated as:
hCM, initial=hA+hB2=0+l22=l4
where hA=0 (the height of A) and hB=l2 (the height of B).
As body A moves upwards, it will continue to rise until the string becomes taut. We need to find the velocity of body B when the string becomes taut.
When the string becomes taut, both bodies will have the same speed v′. By conservation of momentum:
mv0+m⋅0=mv′+mv′
This simplifies to:
v0=2v′
Thus, we find:
v′=v02=√6gl2=√62√gl
The center of mass will rise with the velocity v′ until both bodies reach their maximum height. The maximum height can be calculated using the kinematic equation:
v2=u2+2as
where v=0 (final velocity at maximum height), u=v′, and a=−g (acceleration due to gravity).
0=(√62√gl)2−2gh
This gives:
0=64gl−2gh
Rearranging gives:
2gh=64gl
h=6l8=3l4
The final height of the center of mass is the initial height of the center of mass plus the height it rises:
hCM, final=hCM, initial+h=l4+3l4=l
The maximum height up to which the center of mass of the system rises is:
l
Topper's Solved these Questions
- CENTRE OF MASS & MOMENTUM CONSERVATIONBook:BANSALChapter:CENTRE OF MASS & MOMENTUM CONSERVATIONExercise:EXERCISE-4 (SECTION-A) (JEE-ADVANCED Previous Year Questions)
Explore 11 Videos
- CENTRE OF MASS & MOMENTUM CONSERVATIONBook:BANSALChapter:CENTRE OF MASS & MOMENTUM CONSERVATIONExercise:EXERCISE-4 (SECTION-A) (Comprehension)
Explore 3 Videos
- CENTRE OF MASS & MOMENTUM CONSERVATIONBook:BANSALChapter:CENTRE OF MASS & MOMENTUM CONSERVATIONExercise:EXERCISE-2[MATRIX TYPE]
Explore 2 Videos
- GRAVITATIONBook:BANSALChapter:GRAVITATIONExercise:EXERCISE -4 Section - B
Explore 6 Videos
Similar Questions
Two particles A and B of equal masses lie close together on a horizontal table and are connected by a light inextensible string of length l. A is projected vertically upwards with a velocity √10gl. Find the velocity with which it reaches the table again.
View SolutionIf two particles of masses m1 and m2 are projected vertically upwards with speed v1 and v2, then the acceleration of the centre of mass of the system is
View Solution
Knowledge Check
Two stones of masses m and 2m are projected vertically upwards so as to reach the same height. The ratio of the kinetic energies of their projection is
A2:1B1:2C4:1D1:4Two bodies are thrown vertically upwards with their initial velocity in the ratio 2:3. Then the ratio of the maximum height attained by them is
A1:1B4:9C2:3D√2:√3A body projected vertically upwards with a velocity of 19.6m/s reaches a height of 19.8 m on earth. If it is projected vertically up with the same velocity on moon, then the maximum height reached by it is
A19.18 mB3.3 mC9.9 mD118.8 m
Two particles of same mass are project simultaneously with same speed 20ms−1 from the top of a tower of height 30m. One is projected vertically upwards and other projected horizontally.The maximum height attained by centre of mass from the ground will be (g=10ms−2)
View SolutionTwo particles of equal mass are projected simultaneously with speeds 20m/s end 10√3m/s as shown in figure. Find the maximum height reached by the centre of mass of the particles
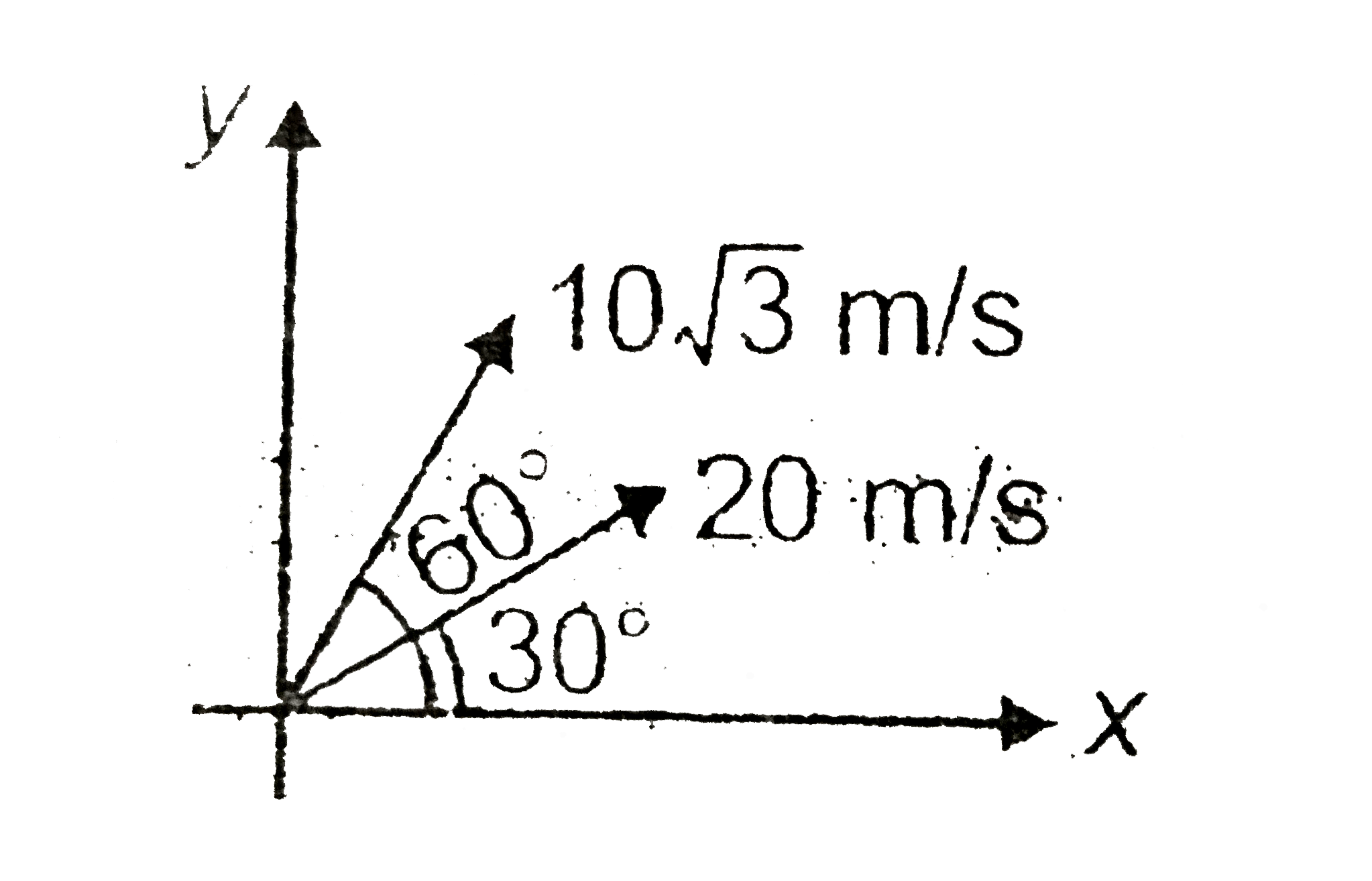
View SolutionA particle of mass m is suspended by a string of length l from a fixed rigid support. Particle is imparted a horizontal velocity u=√2gl. Find the angle made by the string with the vertical when the acceleration of the particle is inclined to the string by 45∘?
View SolutionA small ball is connected to a block by a light string of length l. Both are initially on the ground. There is sufficient friction on the ground to prevent the block from slipping. The ball is projected vertically up with a velocity u, where 2gl<u2<3gl. The centre of mass of the block + ball' system is C.

View SolutionA body is projected vertically upwards with a speed of √GMR ( M is mass and R is radius of earth ) . The body will attain a height of
View Solution

