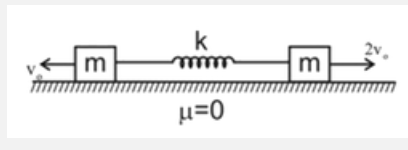
Two identical blocks of mass m, each are connected by a spring as shownin the figure. At any instant of time t=0, one block is given a velocity v1 and other is given a velocity v2(v1>v2) in the same direction simultaneously as shown in the figure. Find the maximum energy stored in the spring.
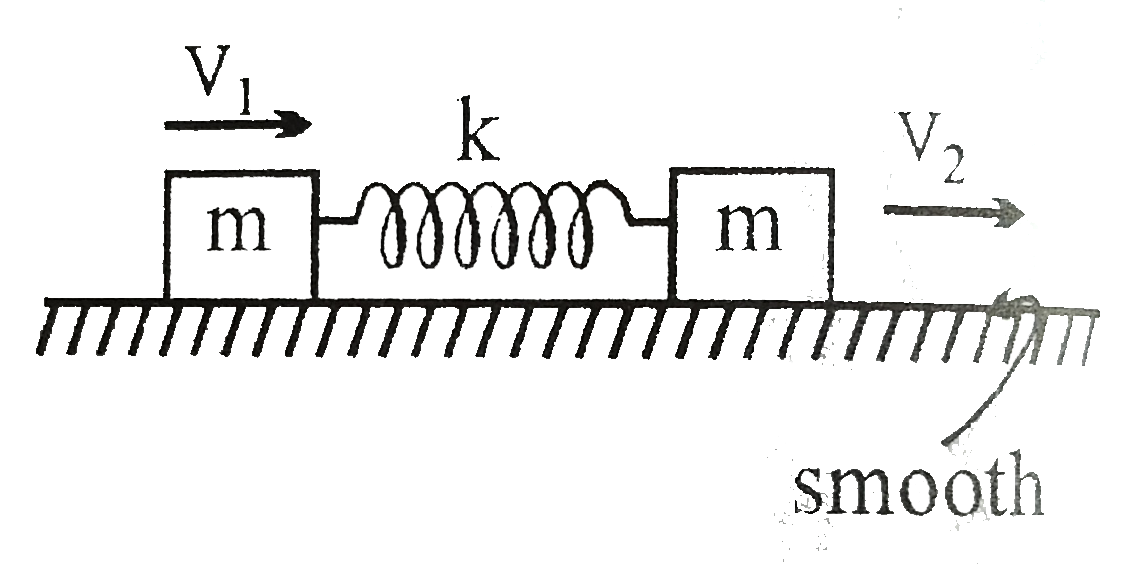
The correct Answer is:14m(v1−v2)2
14μv2rel=12kx2max=Umax
⇒Umax=12((m)(m)m+m)(v2−v1)2=14m(v1−v2)2
Topper's Solved these Questions
- CENTRE OF MASS & MOMENTUM CONSERVATIONBOOK - BANSALCHAPTER - CENTRE OF MASS & MOMENTUM CONSERVATIONEXERCISE - EXERCISE-4 (SECTION-A) (JEE-ADVANCED Previous Year Questions)
11 Videos
- CENTRE OF MASS & MOMENTUM CONSERVATIONBOOK - BANSALCHAPTER - CENTRE OF MASS & MOMENTUM CONSERVATIONEXERCISE - EXERCISE-4 (SECTION-A) (Comprehension)
3 Videos
- CENTRE OF MASS & MOMENTUM CONSERVATIONBOOK - BANSALCHAPTER - CENTRE OF MASS & MOMENTUM CONSERVATIONEXERCISE - EXERCISE-2[MATRIX TYPE]
2 Videos
- GRAVITATIONBOOK - BANSALCHAPTER - GRAVITATIONEXERCISE - EXERCISE -4 Section - B
6 Videos
Similar Questions

A block of mass 200 g is given velocity 2(m)/(s) on a horizontal surface as shown in the figure. Find the maximum compression of spring of spring constant k=100(N)/(m)
View SolutionTwo masses are connected by a spring as shown in the figure. One of the masses was given velocity v = 2 k, as shown in figure where 'k' is the spring constant. Then maximum extension in the spring will be
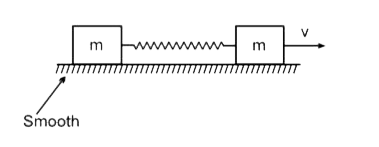
View Solution
Knowledge Check
Two identical blocks of mass m, each are connected by a spring as shown in figure. At any instant of t = 0, one block is given a velocity V0 and other is given a velocity 2V0 in the same direction simultaneously as shown in figure. The maximum energy stored in spring
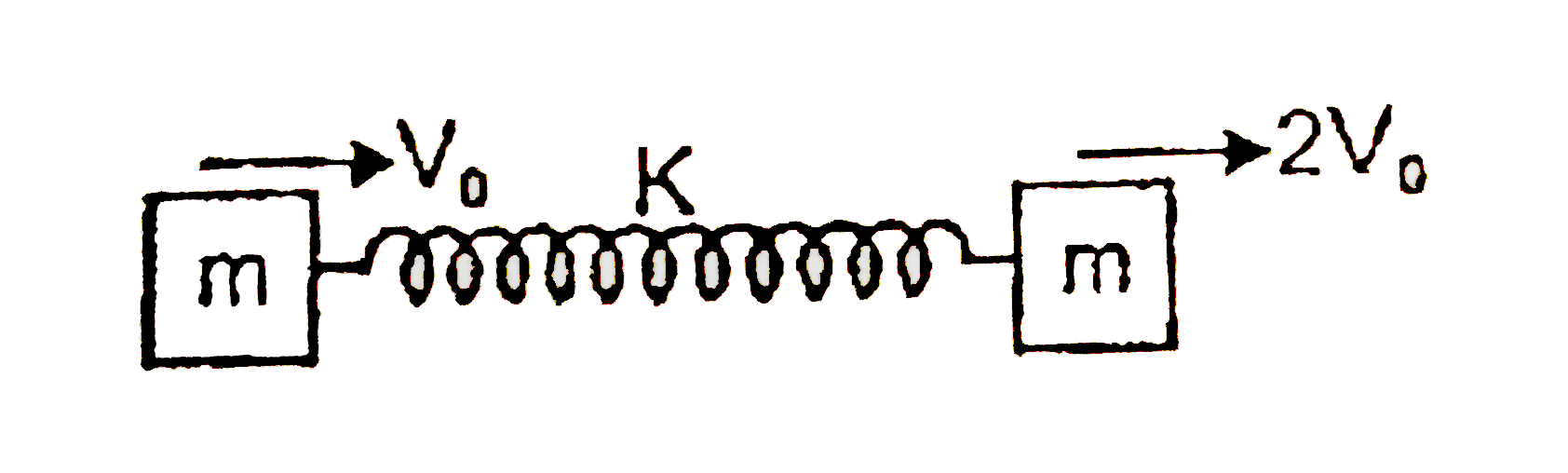 A12mV20B14mV20C34mV20D52mV20
A12mV20B14mV20C34mV20D52mV20Blocks A&B of mass m each are connected with spring of constant k both blocks lie on frictionless ground and are imparted horizontal velocity v as shown when spring is unstretched find the maximum stretch of spring.
 Av√mkBv√m2kCv√2mkDnone
Av√mkBv√m2kCv√2mkDnoneTwo masses A and B of mass M and 2M respectively are connected by a compressed ideal spring. The system in placed on a horizontal frictionless table and given a velocity uˆk in the z-direction as shown in the figure. The spring is then released. In the subsequent motion the line from B to A alwyas points along the ˆi unit vector. All some instant of time mass B has a x-component of velocity as vxˆi. The velocity →vA of mass A at that instant is :-
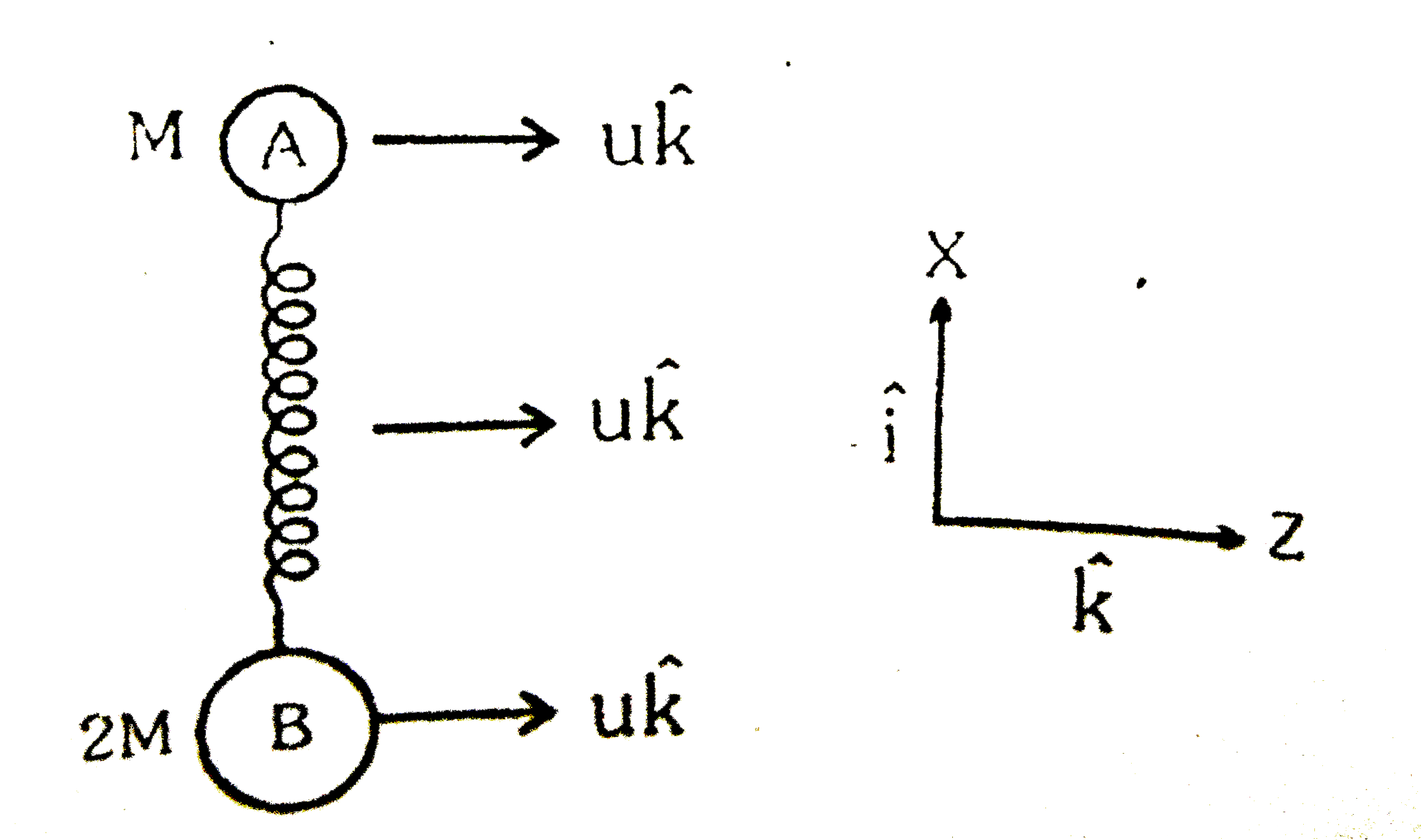 Avxˆi+uˆkB−vxˆi+uˆkC−2vxˆi+uˆkD2vxˆi+uˆk
Avxˆi+uˆkB−vxˆi+uˆkC−2vxˆi+uˆkD2vxˆi+uˆk
The figure shows two blocks of mass m each, connected by an ideal unstretched spring and then placed on a frictionless floor. If the blocks are given velocities v0and2v0 as shown, then the maximum extension in the spring is
View SolutionA block of mass m held touching the upper end of a light spring of force constant K as shown in figure. Find the maximum potential energy stored in the spring if the block is released suddenly on the spring.

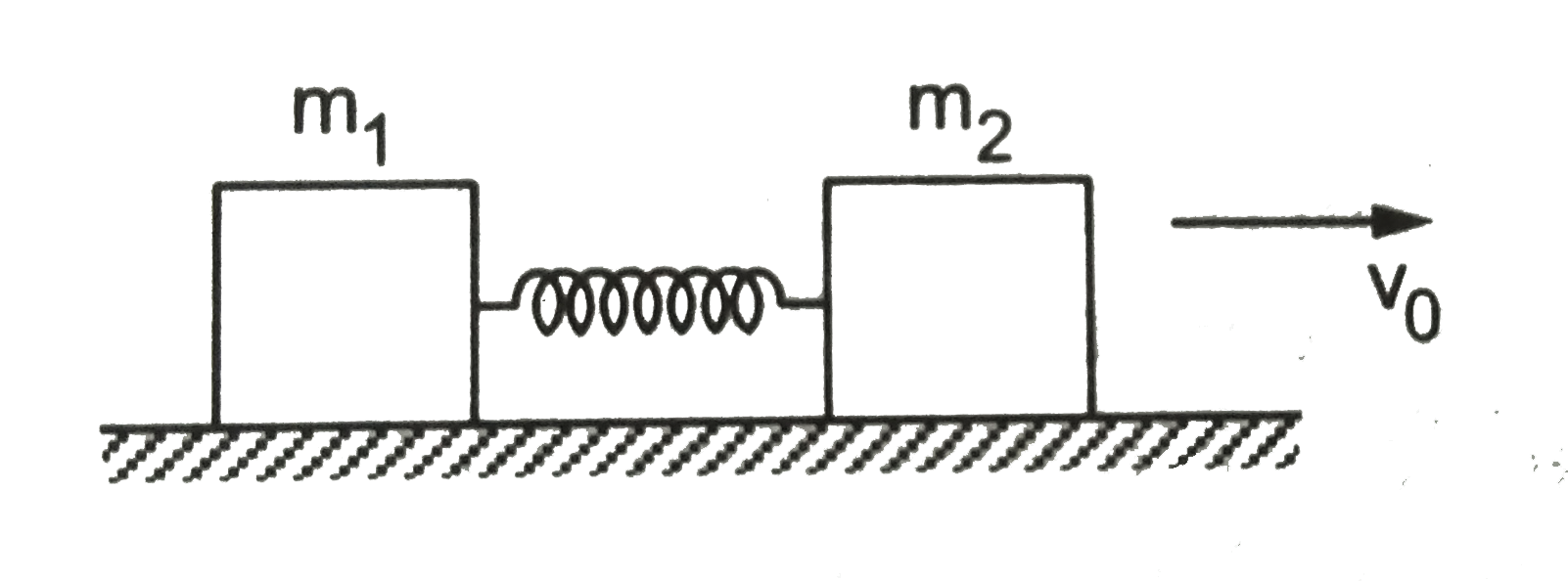
View SolutionTwo blocks of masses m1andm2 are connected by a spring of spring constant k figure. The block of mass m2 is given a shapr imulse so that it acquires a velocity v0 twoards right. Find a. the velocity of the cenre of mas b. the maximum elongation that teh spring will suffer.
View SolutionA dumbbell consists of two balls A and B of mass m=1 kg and connected by a spring. The whole system is placed on a smooth horizontal surface as shown in the figure. Initially the spring is at its natural length, the ball B is imparted a velocity v0=8√7m/s in the direction shown. The spring constant of the spring is adjusted so that the length of the spring at maximum elongation is twice that of the natural, length of the spring. Find the maximum potential energy stored (in Joule) in the spring during the motion.

View SolutionA small block of mass m is plced over a long plank of mass M the coefficient of friction between then is μ ground is smooth At t=0m is given a velocity v1 and M a velocity v2(>v1) as shown in figure After this M is maintained at constant celeration a(<μg)
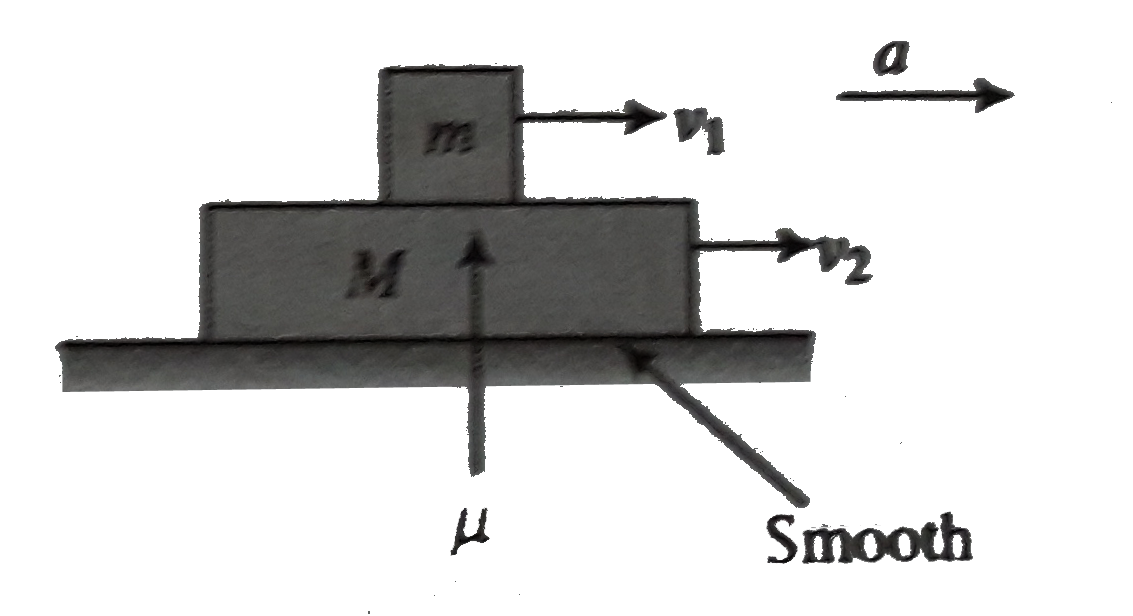
Initially there will be some relative motion between the block and the plank ,but after some time relative motion will cease and velocities of both will become
Draw the velocition of velocity of block as a function of time.
View Solution
