A projectile is fired at a speed of 100 m/s at an angel of 370 above the horizontal. At the highest point, the projectile breaks into two parts of mass ratio 1:3 the smaller coming to rest. Find the distance from the launching point to the where the heavier piece lands.
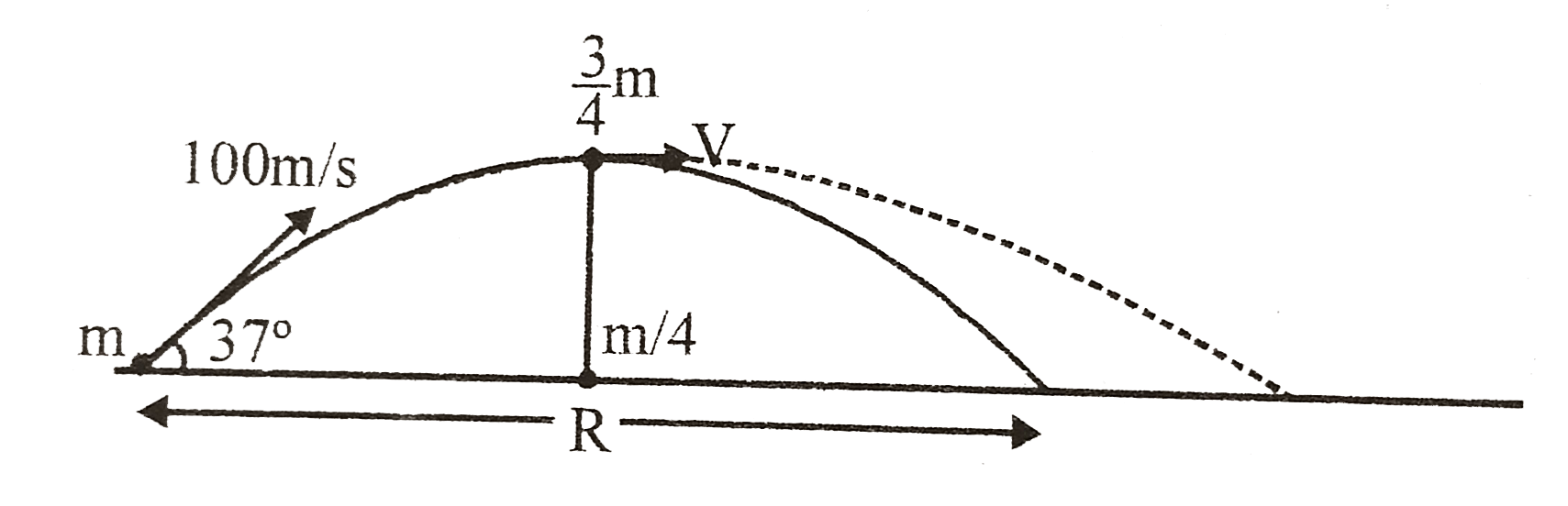
As there is no external force in horizontal direction, (Psys)xis conserved let the horizontal velovity of heavier mass at the highest point be v Applying conservation of momentum in x - direction, at highest point,
(m×ucos37∘)=(m4×0+3m4×v)
⇒ v=3203m/s
for projectile time to reach highest point and time to reach ground are equal toT2
for time of flight T, using concept of projectile motion,
T=2usinθg
T=12sec,
∴ T/2=6sec
∴horizontal distance travelled in first 6 sec. & next 6 sec is (ucos37∘×6)&(v×6) respectively
x=480+640
=1120m
Topper's Solved these Questions
- CENTRE OF MASS & MOMENTUM CONSERVATIONBOOK - BANSALCHAPTER - CENTRE OF MASS & MOMENTUM CONSERVATIONEXERCISE - Solved Examples
15 Videos
- CENTRE OF MASS & MOMENTUM CONSERVATIONBOOK - BANSALCHAPTER - CENTRE OF MASS & MOMENTUM CONSERVATIONEXERCISE - Practice Exercise
20 Videos
- GRAVITATIONBOOK - BANSALCHAPTER - GRAVITATIONEXERCISE - EXERCISE -4 Section - B
6 Videos
Similar Questions
A projectile is fired at a spedd of 100 m/s at an angel of 370 above the horizontal. At the highest point, the projectile breaks into two parts of mass ratio 1:3 the smaller coming to rest. Findthe distance from the launching point to the where the heavier piece lands.

View SolutionA bomb is thrown at a speed 20m/s at an angle 45∘. At the highest point , it explodes into two parts of equal mass , the one part coming to rest. Find the distance from the origin to the point where the other part strikes the ground.
View Solution
Knowledge Check
A bullet fired from gun with a velocity 30 m/s at an angle of 60∘ with horizontal direction. At the highest point of its path, the bullet explodes into two parts with masses in the ratio 1 : 3. The lighter mass comes to rest immediately. Then the speed of the heavier mass is
A30 m/sB20 m/sC10 m/sD5 m/sA projectile of mass 20 kg is fired with a velocity of 400m/sat an angle of 45∘ with the horizontal .At the highest point of the trajectocy the projectile explodes into two fragments of equal mass,one of which falls vertically downward with zero initial speed, The distance of the point where the other fragment falls from the point offiring is:
A24000 mB16000 mC32000 mD8000 mA particle is projected such that its horizontal range would be R. At the highest point, the particle breaks into two identical parts P and Q. If P comes to rest, the horizontal distance of point from the point of projection (i.e. origin) where the particle Q lands on the ground is
A1.5 RBRC2.5 RD2 R
A body is projected with a speed 160 m/s at an angle 53∘ with the horizontal, At the highest point, body explodes into two pieces with mass ratio 1:3. Smaller piece comes to rest immediately after explosion. Find the distance of point from point of projection where heavier piece strikes the horizontal surface.
View SolutionA particle is projected at an angle of60∘ above the horizontal with a speed of 10m/s .When the projectile reaches highest point, change in velocity is
View SolutionAn object of mass 5 kg is projected with a velocity of 20 m/s at angle of 60° to the horizontal. At the highest point of its path, the projectile explodes and breaks up into two fragments of masses 1 kg and 4 kg. The fragments separate horizontally after the explosion. The explosion releases internal energy such that the kinetic energy of the system at the highest point is doubled. If the separation between the two fragments when they reach the ground is x, then find the value of x5√3.
View SolutionA projectile of mass "m" is projected from ground1 with a speed of 50 m/s at an angle of 53∘ with the horizontal. It breaks up into two equal parts at the highest point of the trajectory. One particle coming to rest immediately after the explosion.
The distance between the pieces of the projectile when they reach the ground are :
View SolutionA particle of mass 3m is projected from the ground at some angle with horizontal. Its horizontal range is R. At the highest point of its path it breaks into two pieces of masses m and 2m respectively. The smallar mass comes to rest. The larger mass finally falls at a distance x from the point of projection where x is equal to
View Solution
