A particle moves along x-axis in positive direction. Its acceleration 'a' is given as a=cx+d, where x denotes the x- coordinate of particle, c and d are positive constants. For velocity position graph of particle to be of type as shown in figure,
the value of speed of particle at x=0 should be 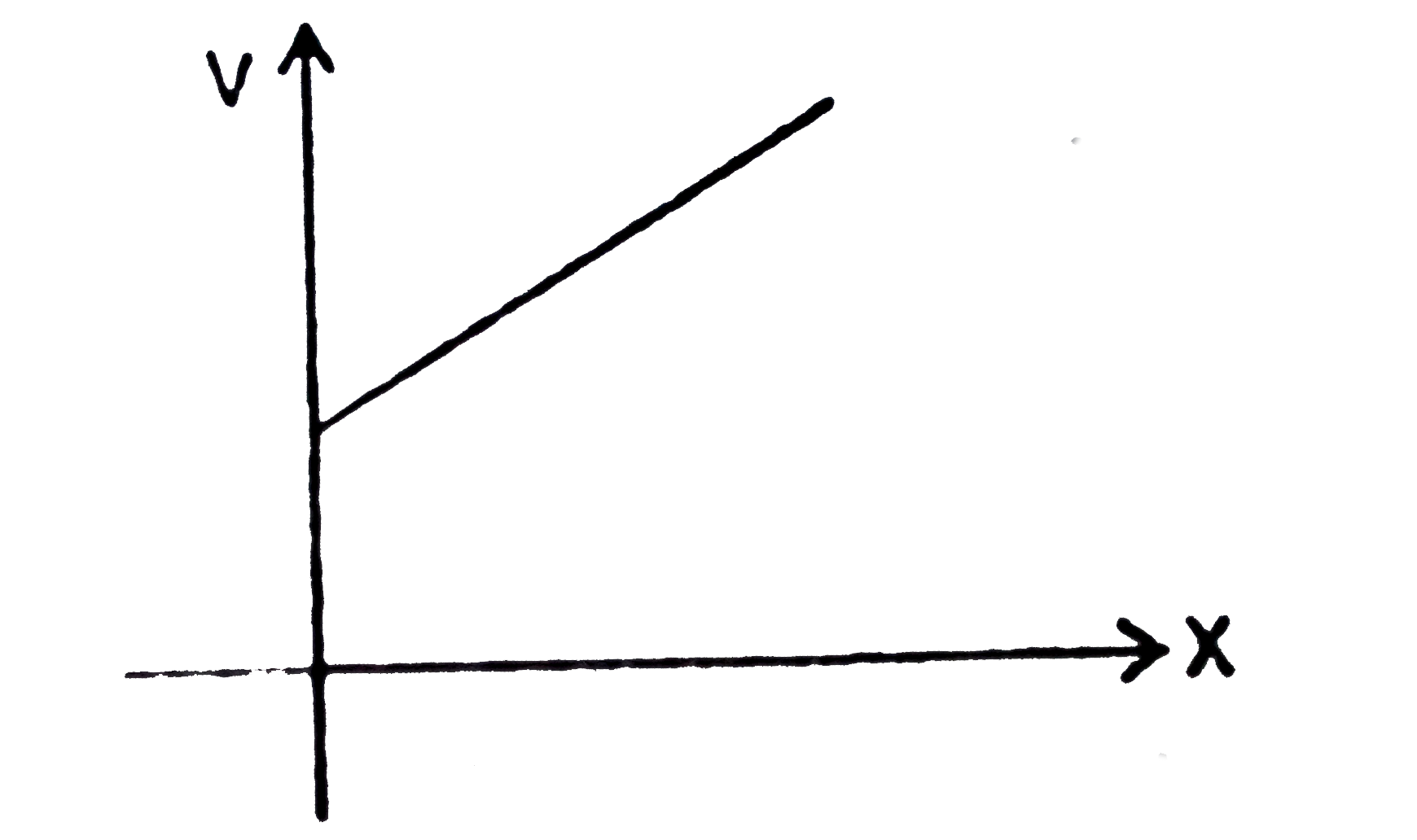
√2d2c
√(8d2c)
√4d2c
√d2c
The correct Answer is:D
a=Vdvdx=cx+d
Let at x=0v=u
∴∫vuvdv=∫x0(cx+d)dx
or v2=cx2+2dx+u2
v shall be linear function of x if cx2+2dx+u2 is perfect square
Topper's Solved these Questions
Similar Questions
Knowledge Check
The velocity –position graph of a particle moving along a straight line is shown. Then acceleration of the particle at s = 15 m is :
 A23ms−2B−23ms−2C203ms−2D−203ms−2
A23ms−2B−23ms−2C203ms−2D−203ms−2Position-time graph for a particle moving along x− direction is as shown in the figure. Average speed of the particle from t=0 to t=4 is :
 A154m/sB103m/sC52m/sD54m/s
A154m/sB103m/sC52m/sD54m/sThe x-t graph of a particle moving along a straight line is shown in figure

The speed-time graph of the particle is correctly shown byA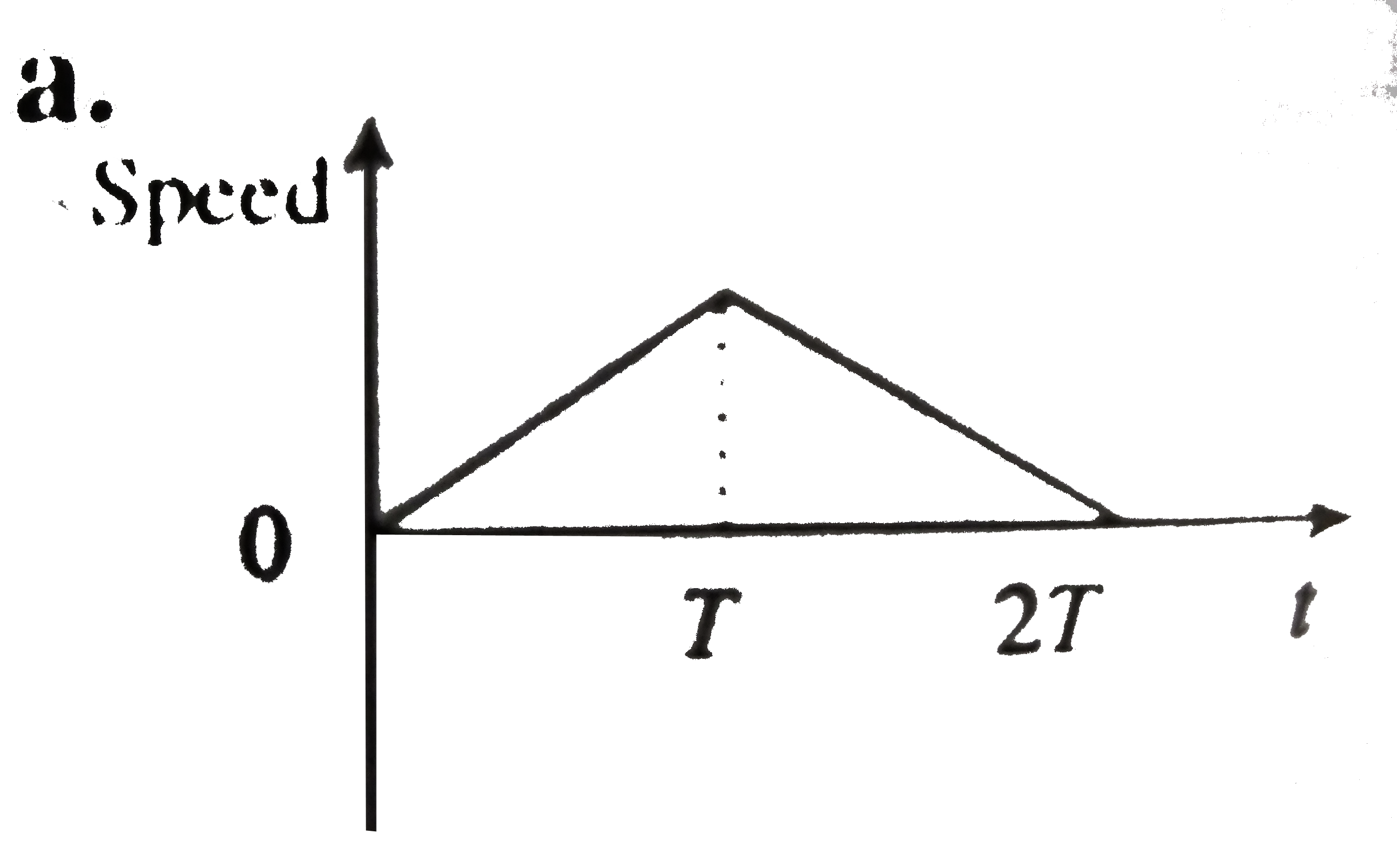 B
B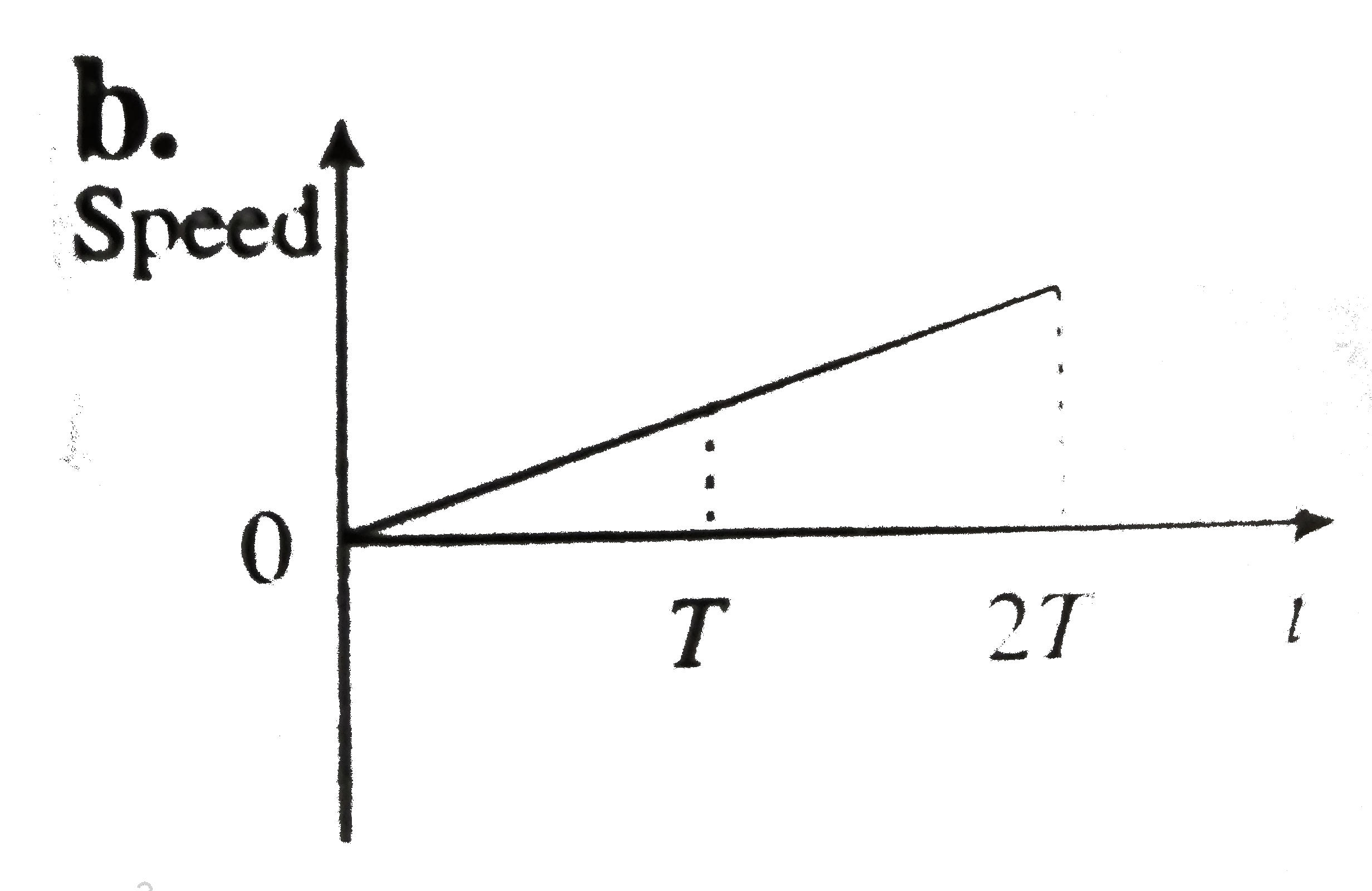 C
C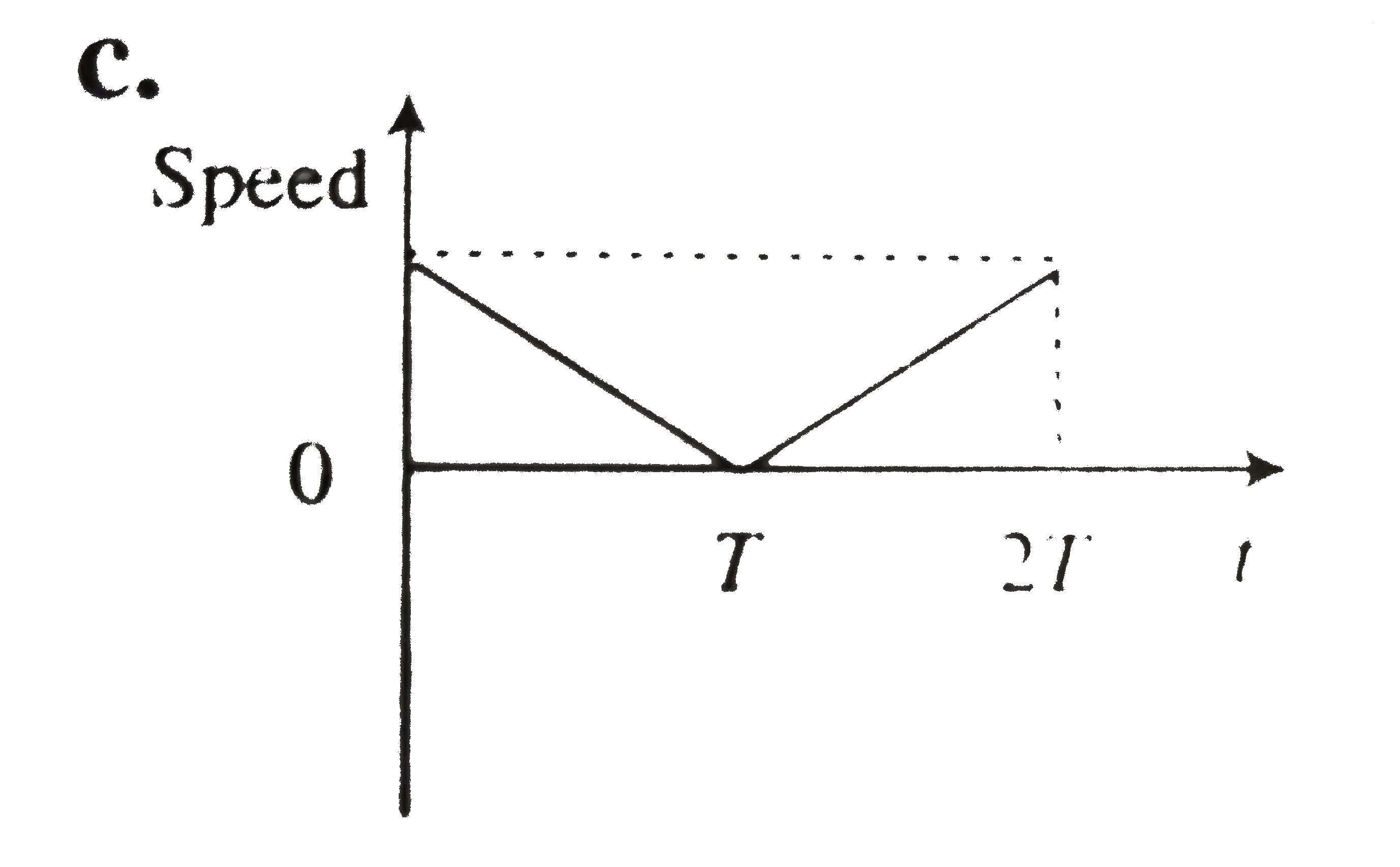 D
D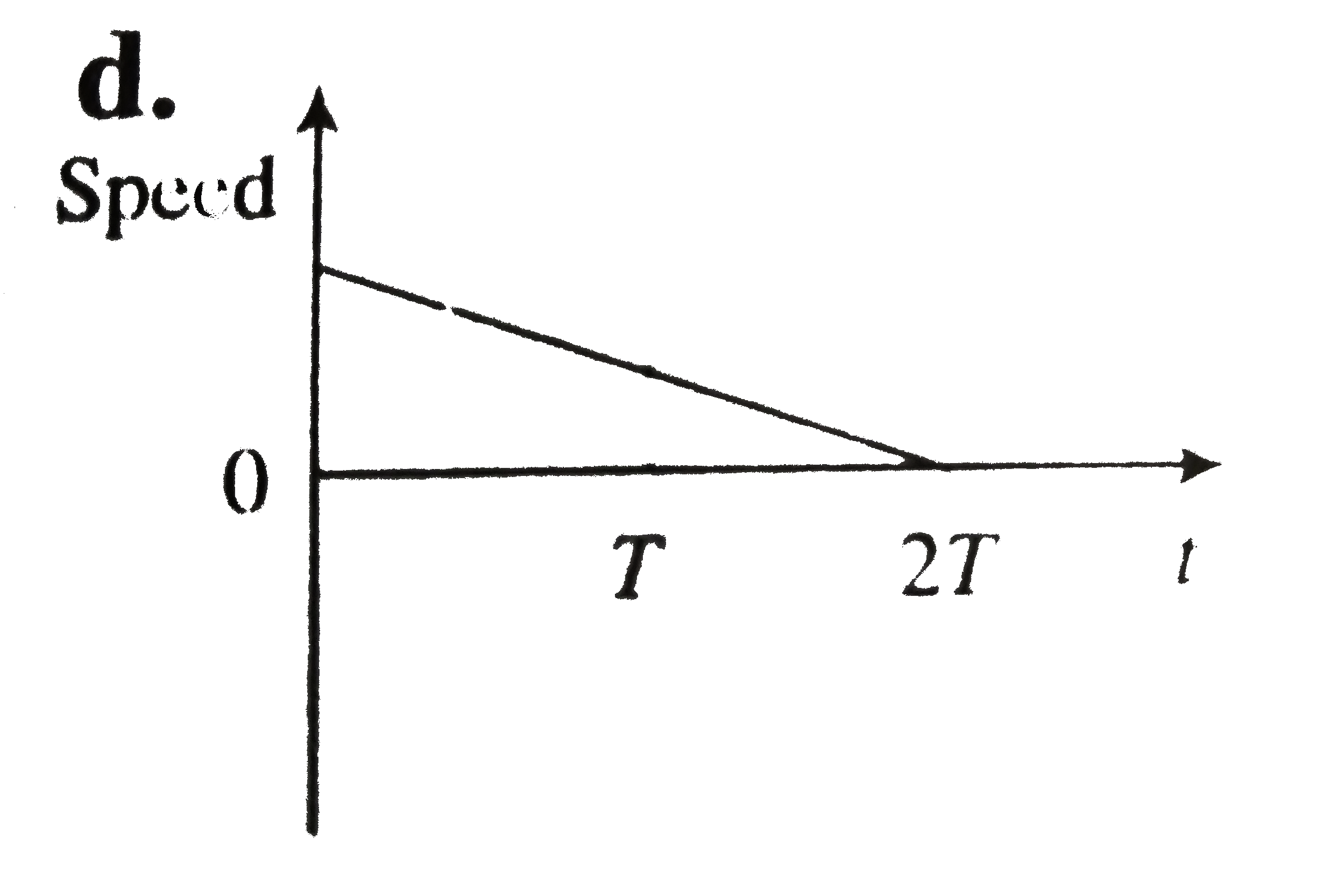
The velocity-position graph of a particle moving in a straight line along x -axis is givenbelow.Acceleration of particle,at x=2m is
View SolutionThe velocity-position graph of a particle moving in a straight line along x-axis is given below. Acceleration of particle at x = 2 m is
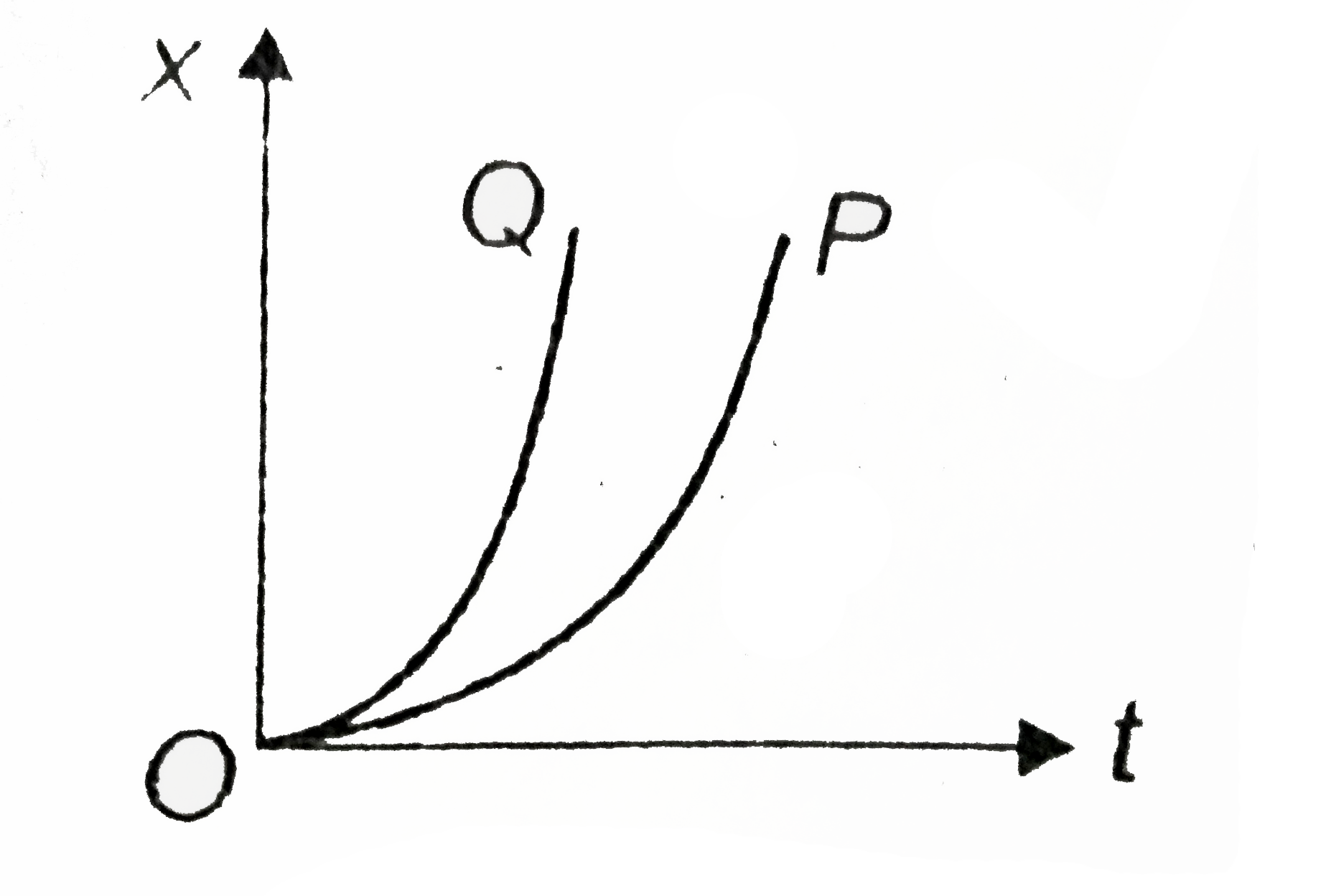
View SolutionThe position-time graph for two particles P and Q moving on x-axis is shown in the figure. Then
View SolutionA particle moves in the xy plane with a constant acceleration ω directed along the negative y-axis. The equation of motion of particle has the form y=cx−dx2, where c and d are positive constants. Find the velocity of the particle at the origin of coordinates.
View SolutionFor a particle moving along x-axis, velocity-time graph is as shown in figure. Find the displacement of the particle?
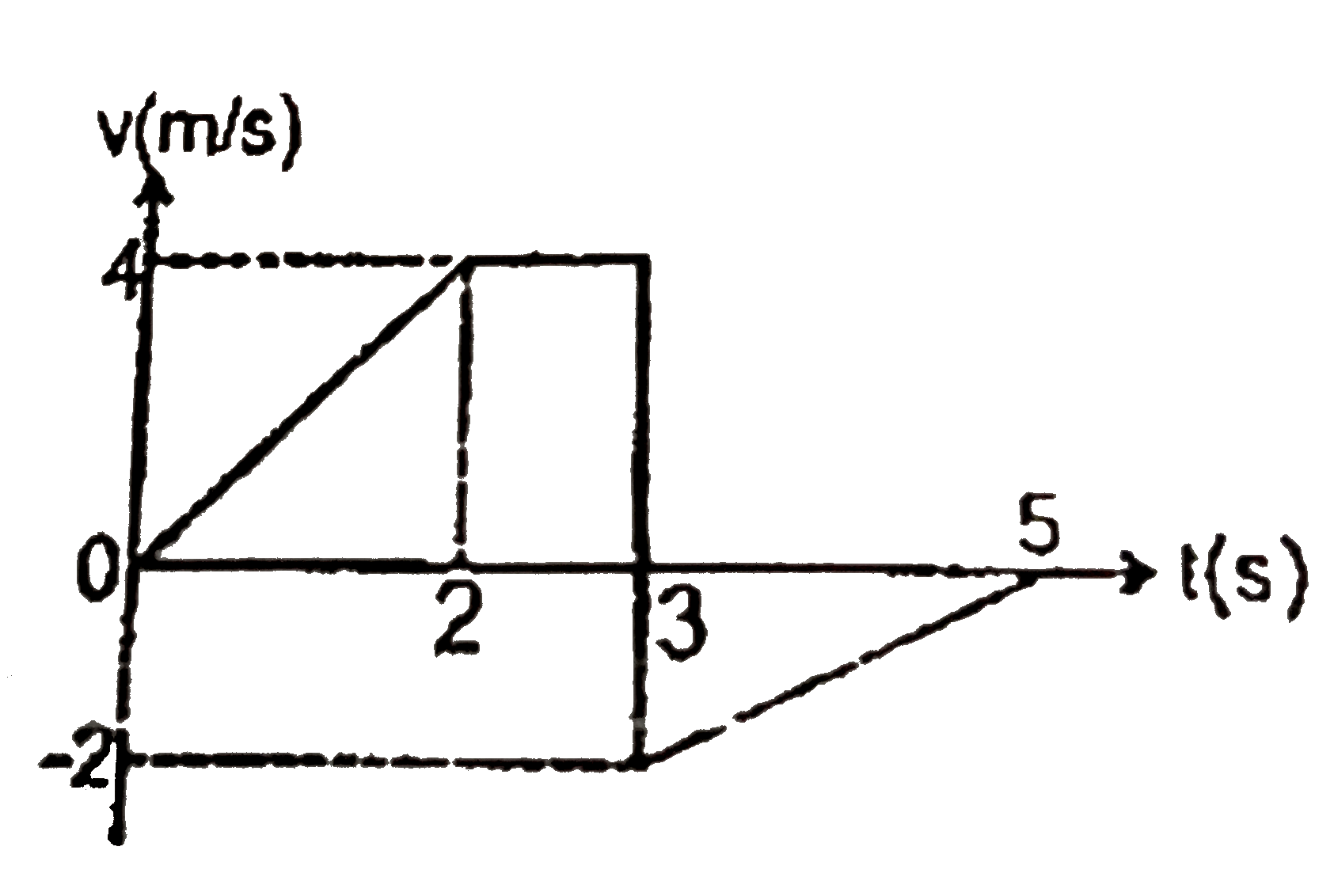
View Solution

