A semi circular disc of radius R is placed on a smooth horizontal surface. Figure shows top view of this. If temperature is increased by Δt then displacement of (coefficient of linear expansion is α): 
B along x-axis is RαΔt
B along y-axis is zero
A along y-axis isRαΔt
A along x- axis is −4R3παΔt
The correct Answer is:B, C, D
Displacement of centre of mass is zero. So take centre of mass as origin then find displacement of all points.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
A uniform metallic disc of radius r and mass m is spinning with angular speed ω0 about an axis passing through its centre and perpendicular to plane. If its temperature is increased (slightly) by ΔT its new angular speed is (The coefficient of linear expansion of the metal is α)
Aω0(1+2αΔT)Bω0(1+αΔT)Cω0(1−2αΔT)Dω0(1−3αΔT) - Question 2 - Select One
A uniform circular disc of radius R is placed on a smooth horizontal surface with its plane horizontal and hinged at circumference through point O as shown . An impulse P is applied at a perpendicular distance h from its centre C. The value of h so that the impulse due to hinge is zero, isARBR/2CR/3DR/4 - Question 3 - Select One
A uniform circular disc of mass 'm' and radius 'R' is placed on a rough horizontal surface and connected to the two ideal non-deformed spring of stiffness k and 2k at the centre 'C' and point 'A' as shown . The centre of the disc is slighty displaced horizontally from equilibrium positon and then released, then the time period of small oscillation of the disc is (there is no slipping between the disc and the surface).
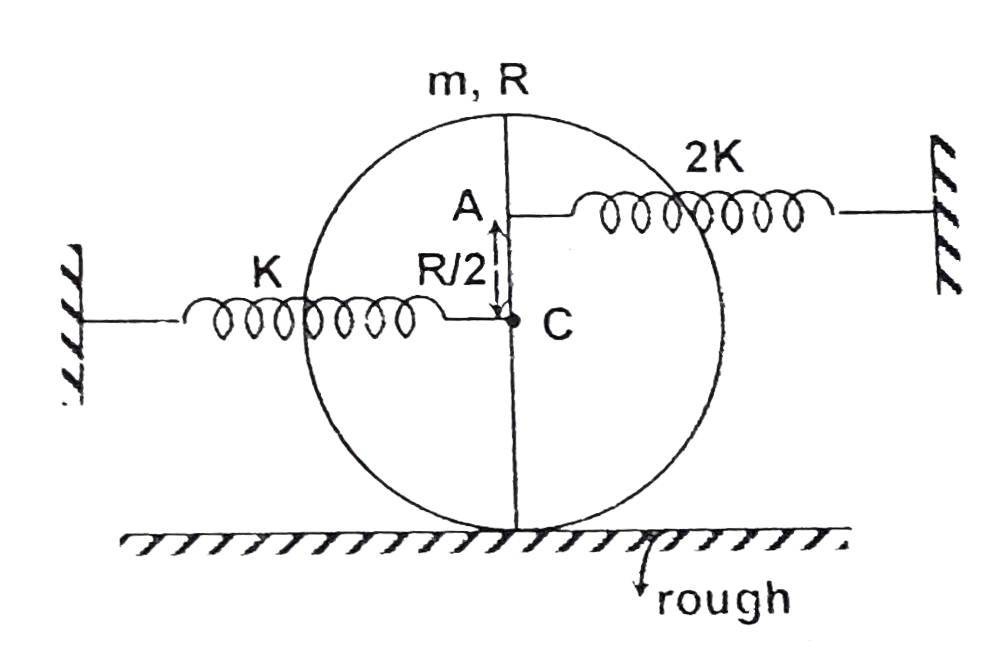A2π√5m7kB2π√3m7kC2π√5m11kD2π√3m11k
A circular disc of radius r is rolling without slipping on a horizontal surface. What is the ratio of the translational KE and rotational KE of disc ?
View SolutionA metal cylinder of radius R is placed on a wooden plank BD. The plank is kept horizontal suspended with the help of two identical string AB and CD each of length L. The temperature coefficient of linear expansion of the cylinder and the strings are a1 and a2 respectively. Angle q shown in the figure is 30∘. It was found that with change in temperature the centre of the cylinder did not move. Find the ratio α1α2 , if it is know that L = 4R. Assume that change in value of θ is negligible for small temperature changes
View SolutionFigure shows a block A of mass 6m having a smooth semicircular groove of radius a placed on a smooth horizontal surface. A block B of mass m is released from a position in groove where its radius is horizontal. Find the speed of the bigger block when the smaller block reaches its bottom most position.
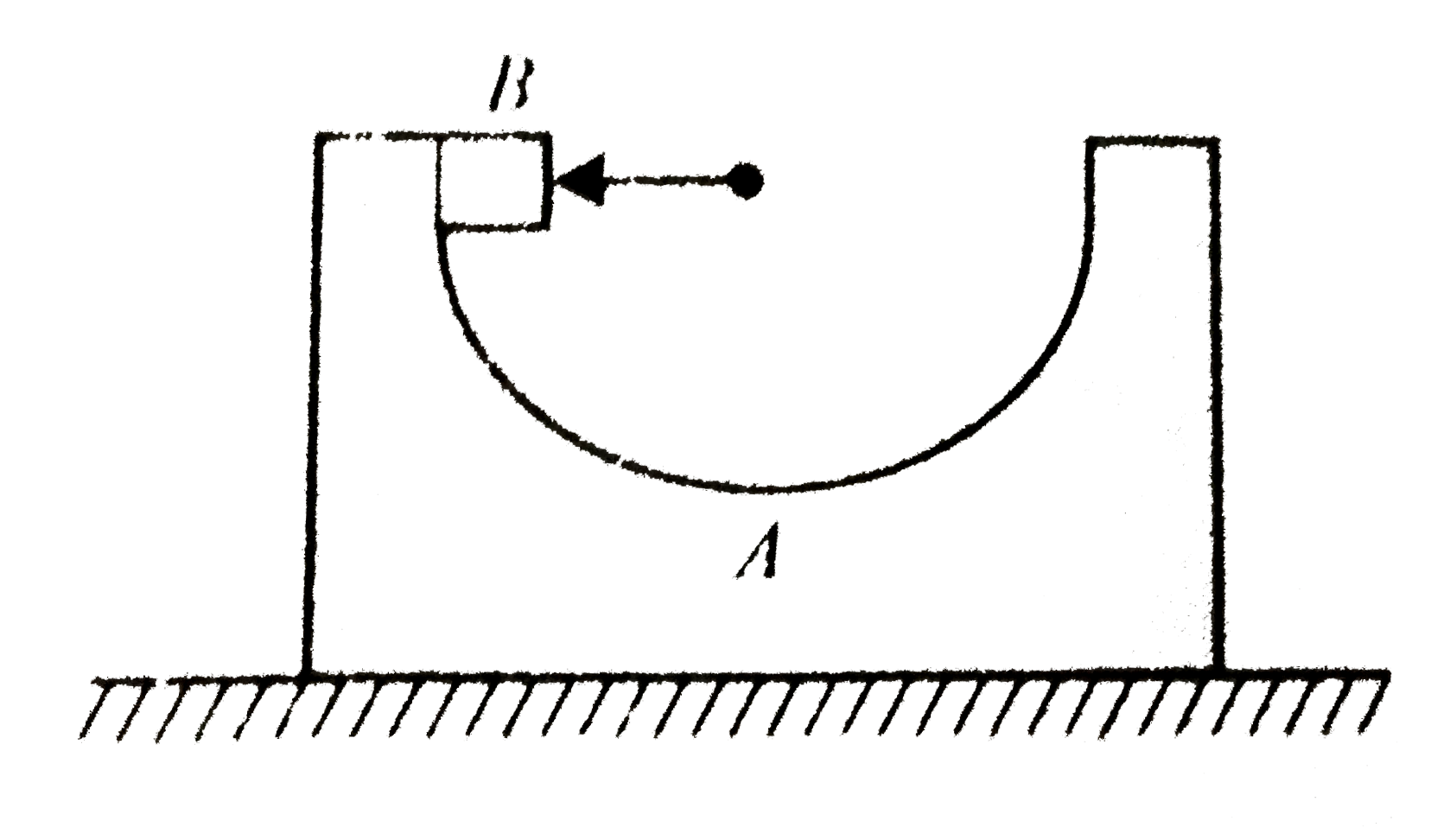
View SolutionThe diameter of a fly wheel is R. Its coefficient of linear expansion is α. If its temperature is increased by δT the percentage increase in its moment of inertia is
View SolutionThe moment of ineratia of a uniform thin rod about its perpendicular bisector is I. If the temperature of the rod is increased by Δt , the moment of inertia about perpendicular bisector increases by (coefficient of linear expansion of material of the rod is α).
View Solution