A particle moves in the $x y$ plane with a constant acceleration $ω$ directed along the negative y-axis. The equation of motion of particle has the form $y = c x - {d x}^{2}$ , where $c$ and $d$ are positive constants. Find the velocity of the particle at the origin of coordinates.

Video Solution

Text Solution

Verified by Experts

Proceed as in the previous problem, here $ω = g$
$= \sqrt{\frac{ω (1 + c^{2})}{2 d}}, θ = {tan}^{- 1} (c)$
OR
$y = c x - d x^{2}$
$\frac{d y}{d t} = c \frac{d x}{d t} - d .2 x \frac{d x}{d t}$
$v_{y} = c v_{x} - 2 d x v_{x}$
$\frac{d v_{y}}{d t} = c \frac{d v_{x}}{d t} - 2 d [x \frac{d v_{x}}{d t} + v_{x} . \frac{d x}{d t}]$
$a_{y} = c . a_{x} - 2 d [x a_{x} + v_{x}^{2}]$
$a_{x} = 0, a_{y} = - ω$
$- ω = - 2 d v_{x}^{2} \Rightarrow v_{x} = \sqrt{\frac{ω}{2 d}}$ (indepedent of $x$ )
$v_{y} = c v_{x} - 2 d x v_{x}$
At origin,
$x = 0, v_{y} = c v_{x} = c \sqrt{\frac{ω}{2 d}}$
$v = \sqrt{v_{x}^{2} + v_{y}^{2}}$
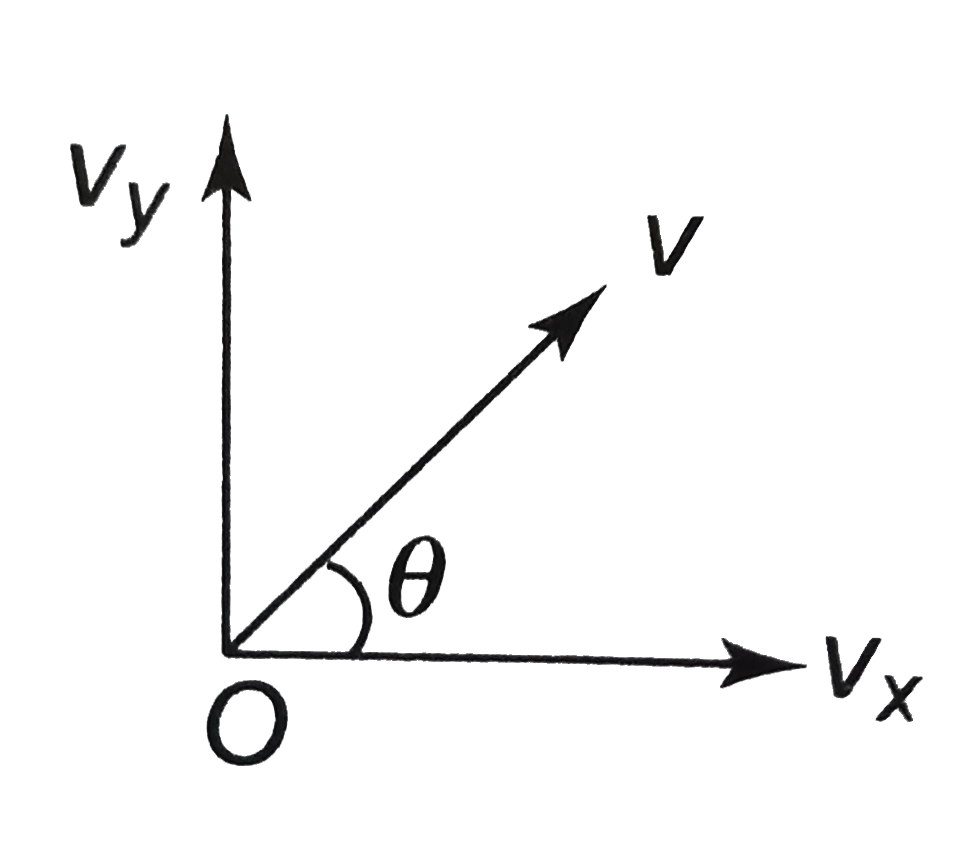
$= \sqrt{\frac{ω}{2 d} + \frac{c^{2} ω}{2 d}} = \sqrt{\frac{ω (1 + c^{2})}{2 d}}$
$tan θ = \frac{v_{y}}{v_{x}} = c \Rightarrow = θ t a^{- 1} (c)$

Updated on:21/07/2023

A particle moves in the $x y$ plane with a constant acceleration 'g' in the negative-direction. Its equqaiton of motion is $y = a x - b x^{2}$ , where $a$ and $b$ are constants. Which of the following are correct?
AThe x-compound of its velocity is constant.
BAt the origin, the y-compound of its velocity is a $\sqrt{\frac{g}{2 b}}$ .
CAt the origin, its velocity makes an angle ${tan}^{- 1}$ (a) with yeh x-axis.
DThe particle moves exactly like a projectile.
A particle moves in a plane with constant acceleration in a direction different from the initial velocity. The path of the particle will be
AA straight will be
BAn arc of a circle
CA parabola
DAn ellipse
A particle moving along the X-axis executes simple harmonic motion, then the force acting on it is given by
where, A and K are positive constants.
A $- A k x$
B $A cos k x$
C $A exp (- k x)$
D $A k x$