A block of mass m compresses a spring iof stifffness k through a distacne l/2 as shown in the figure .If the block is not fixed to the spring the period of motion of the block is

2π√mk
(π+4)√mk
(1+π)√mk
None of these
The period of oscillation =2π√mk
⇒ The period of motion till the block is in contact with the spring is
t=T2=π√mk then it leaves the spring with a speed v=ωA
v=(√km)(l2)
Then it moves with constant velocity v for a distance D=l+l=2l
⇒ The corresponding time of motion =t2=2l/v
⇒t2=2ll2√km=4√mk
∴ The time period of motion =t=t1+t2=π√mk+4√mk
=√mk[π+4].
Topper's Solved these Questions
Similar Questions
A block of mass m moving at a speed v0 compresses a spring of spring constant k as shown in the figure. Find (a) the maximum compression of spring and (b) speed of the block when the spring is compressed to half of maximum compression.
View SolutionA block of mass m is released from rest onto a spring. A having stiffness kA=mg/2h as shown in figure. If the block compresses spring B through a distance h, find the:

a. stiffness of the spring B
b. equilibrium position of the block
c. maximum velocity of the block
d. maximum acceleration of the block
View Solution
Knowledge Check
A block of mass m is at rest on an another block of same mass as shown in figure lower block is attached to the spring than the maximum amplitude of motion so that both the block will remain in contact is
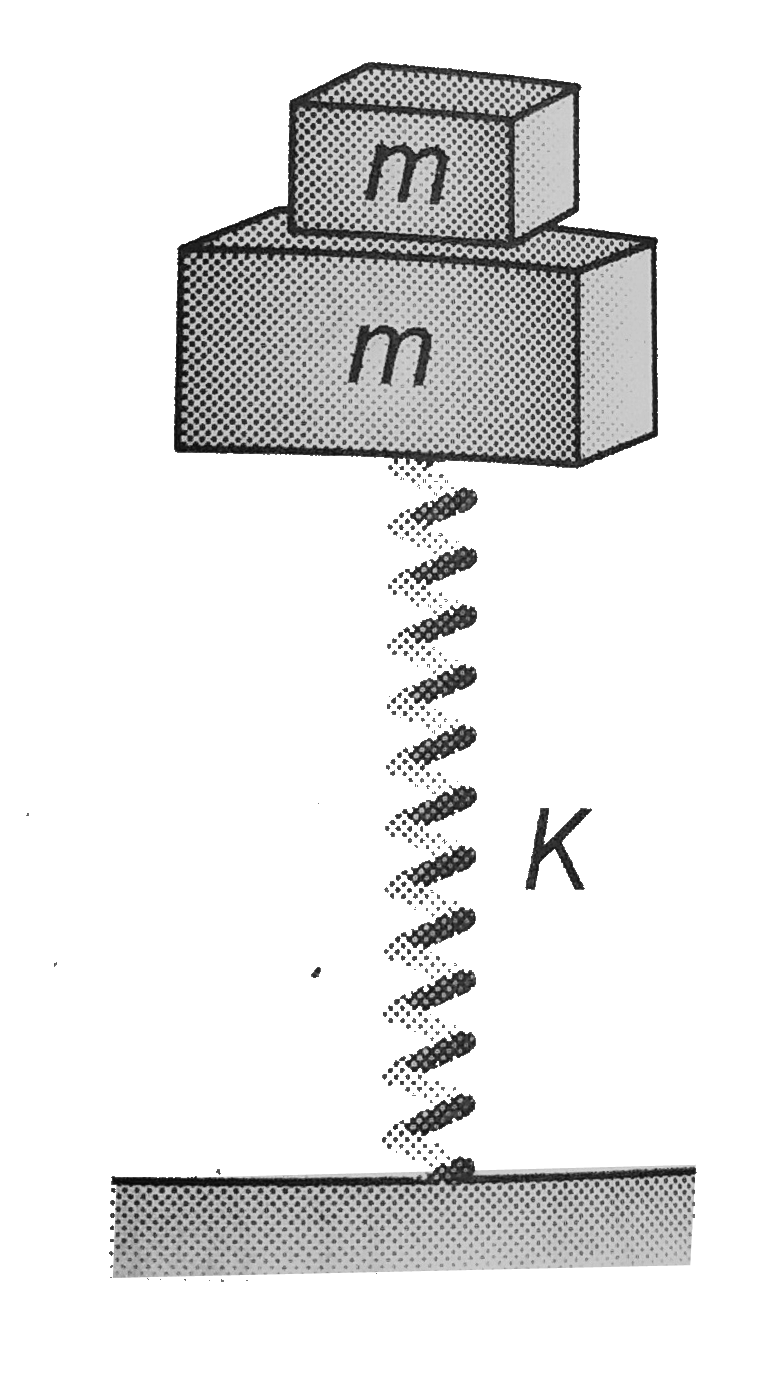 Amg2kBmgkC2mgkD3mg2k
Amg2kBmgkC2mgkD3mg2kA block of mass m rigidly attached with a spring k is compressed through a distance A. If the block is released, the period of oscillation of the block for a complete cycle is equal to
 A4π3√mkBπ√2√mkC2π3√mkDNone of these
A4π3√mkBπ√2√mkC2π3√mkDNone of theseTwo springs are in a series combination and are attached to a block of mass 'm' which is in equilibrium. The spring constants and extension in the springs are as shown in the figure. Then the force exerted by the spring on the block is :
 Ak1k2k1+k2(x1+x2)Bk1x1+k2x2Ck1x1DNone of these
Ak1k2k1+k2(x1+x2)Bk1x1+k2x2Ck1x1DNone of these
A block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. The other end of the spring is fixed, as shown in the figure. The block is initally at rest in its equilibrium position. If now the block is pulled withe a constant force F, the maximum speed of the block is :

View SolutionA block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. The other end of the spring is fixed, as shown in the figure. The block is initally at rest in its equilibrium position. If now the block is pulled withe a constant force F, the maximum speed of the block is :

View SolutionA block of mass m held touching the upper end of a light spring of force constant K as shown in figure. Find the maximum potential energy stored in the spring if the block is released suddenly on the spring.

View SolutionA block of mass m moving with a velocity v0 on a smooth horizontal surface strikes and compresses a spring ofstiffuess k till mass coines to rest as shown in the figure. This phenomenon is observed by two observers :
(a) Standing on the horizontal surface
(b) standing on the block
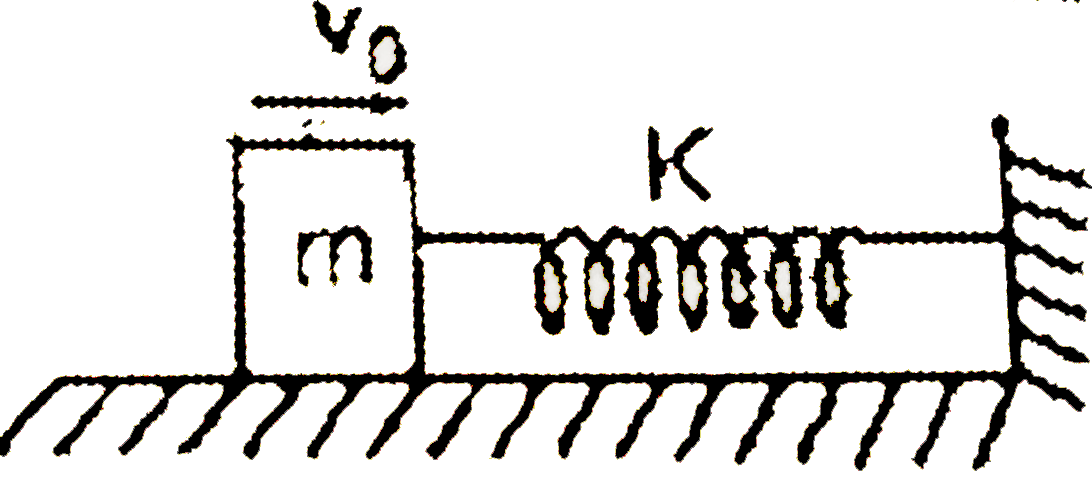
To an observer B, when the block is compressing the spring :
View SolutionTwo blocks of masses m1 and m2 are kept on a smooth horizontal table as shown in figure. Block of mass m1 (but not m2 is fastened to the spring. If now both the blocks are pushed to the left so that the spring is compressed a distance d. The amplitude of oscillatin of block of mass m1 after the system is released is
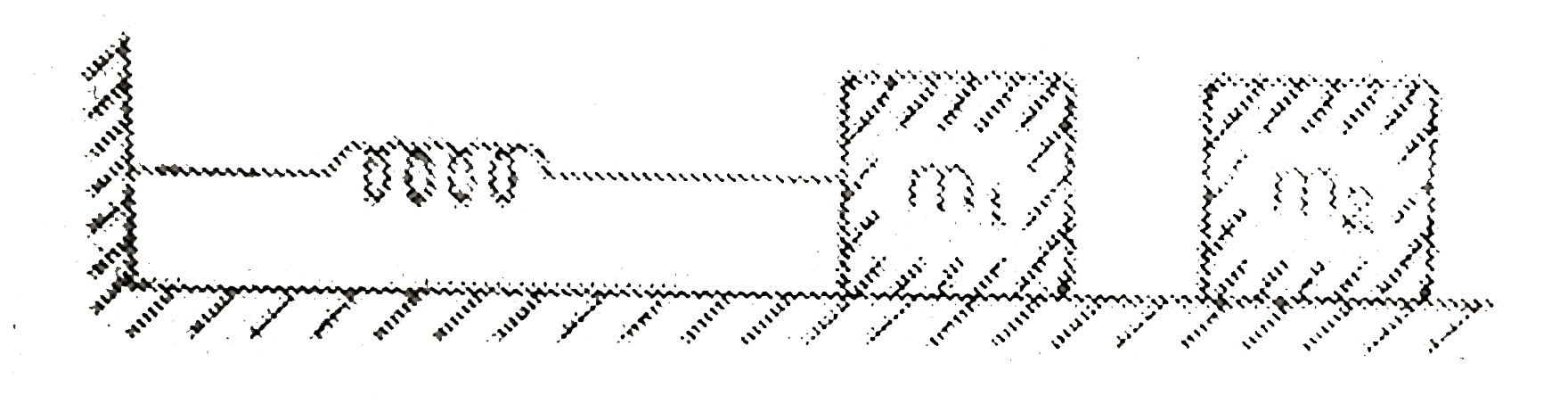
View Solution
