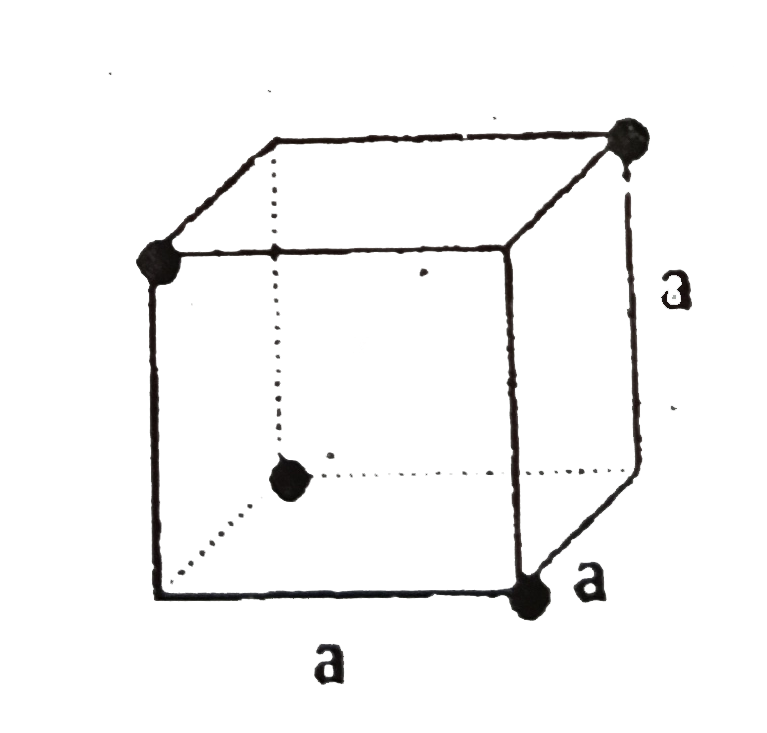
Figure shows 4 identical masses of mass m, arranged on a cube as shown.
The potential energy of the system is
it will collide with one of the masses
It execute an oscillatory motion (not SHM)
It executes SHM
none of these
PE=6×GM2√2a
=−3√2GM2a
F=3×GM22a2×√2√3=√32GM2a2
Topper's Solved these Questions
- GMP ASSESMENTBook:FIITJEEChapter:GMP ASSESMENTExercise:Numerical Based
Explore 61 Videos
- GMP ASSESMENTBook:FIITJEEChapter:GMP ASSESMENTExercise:Multiple Question
Explore 58 Videos
- GENERAL PHYSICSBook:FIITJEEChapter:GENERAL PHYSICSExercise:MATRIX MATCH TYPE
Explore 3 Videos
- GRAVITATIONBook:FIITJEEChapter:GRAVITATIONExercise:Numerical based Question
Explore 2 Videos
Similar Questions
Knowledge Check
Figure shows 4 identical masses of mass m, arranged on a cube as shown.
The force on any particle isA32GM2a2B√32GM2a2C√6GM2a2Dnone of theseA particle of mass m is moved from A to B as show in figure. Then potential energy of the the particle
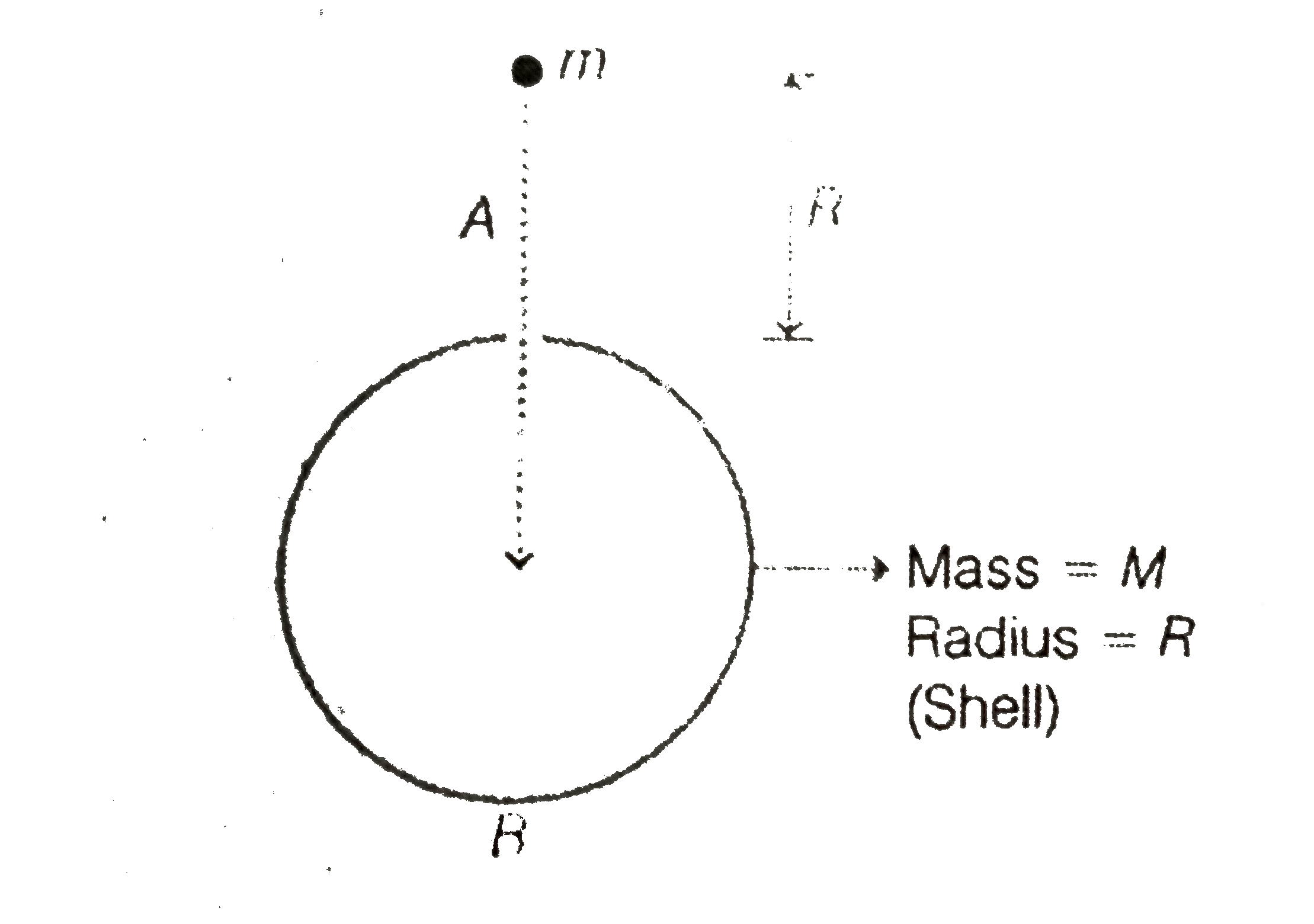 Awill continuously increasesBwill continuously decreasesCwill first increase and then become constantDwill first decreases and then become constant
Awill continuously increasesBwill continuously decreasesCwill first increase and then become constantDwill first decreases and then become constantA ring of mass m is rolling without slipping with linear velocity v as shown is figure. A rod of identical mass is fixed alone one of its diameter. The total kinetic energy of the system is
 A75mv2B23mv2C43mv2D53mv2
A75mv2B23mv2C43mv2D53mv2
Three spheres, each mass M and radius R, are arranged as shown in the figure . The moment of inertia of the system will be

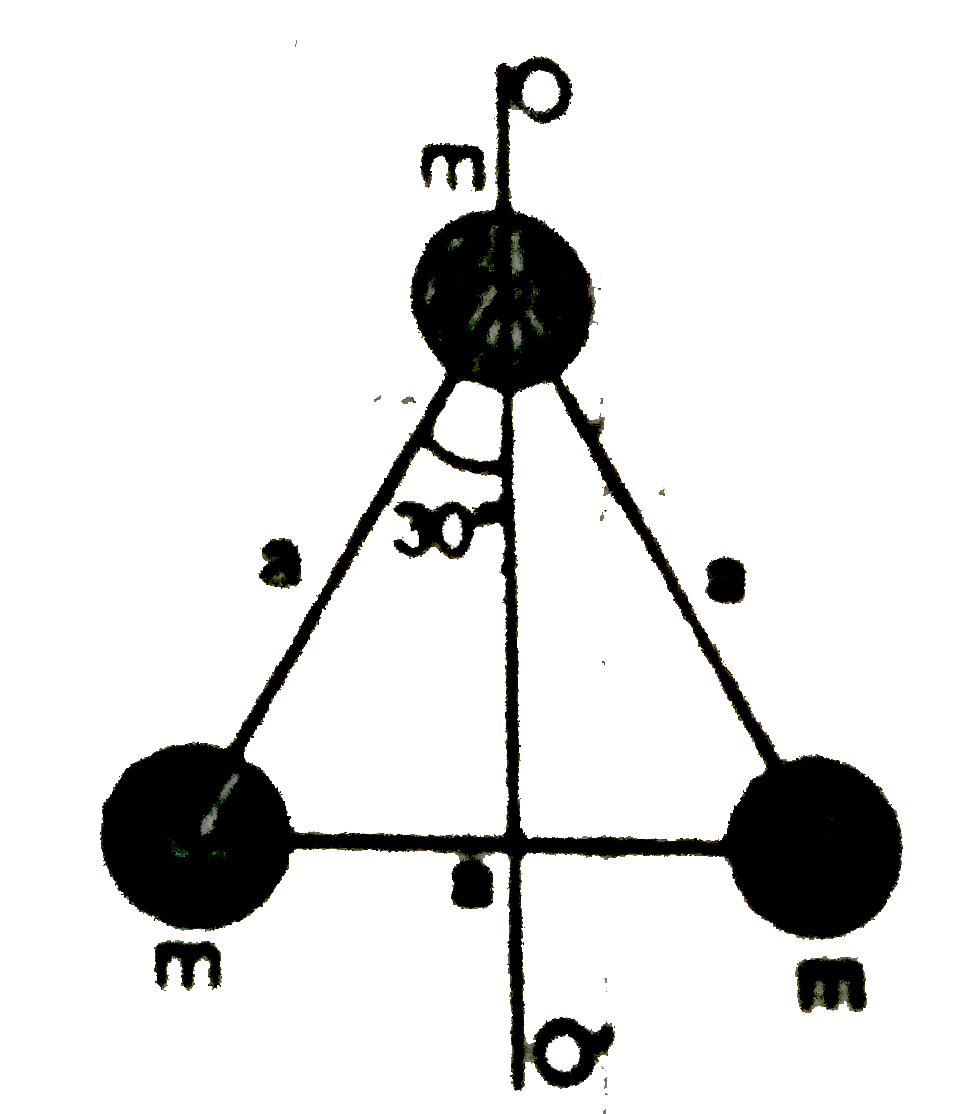
View SolutionThree point masses are arranged as shown in the figure. Moment of inertia of the system about the axis OO' is
View SolutionA system of two identical rods (L-shaped) of mass m and length l are resting on a peg P as shown in the figure. If the system is displaced in its plane by a small angle θ,find the period of oscillations:

View SolutionA rope of length l and mass 'm' is connected to a chain of length l and mass 2m and hung vertically as shown. What is the change in graviational potential energy if the system is inverted and hung from same point.
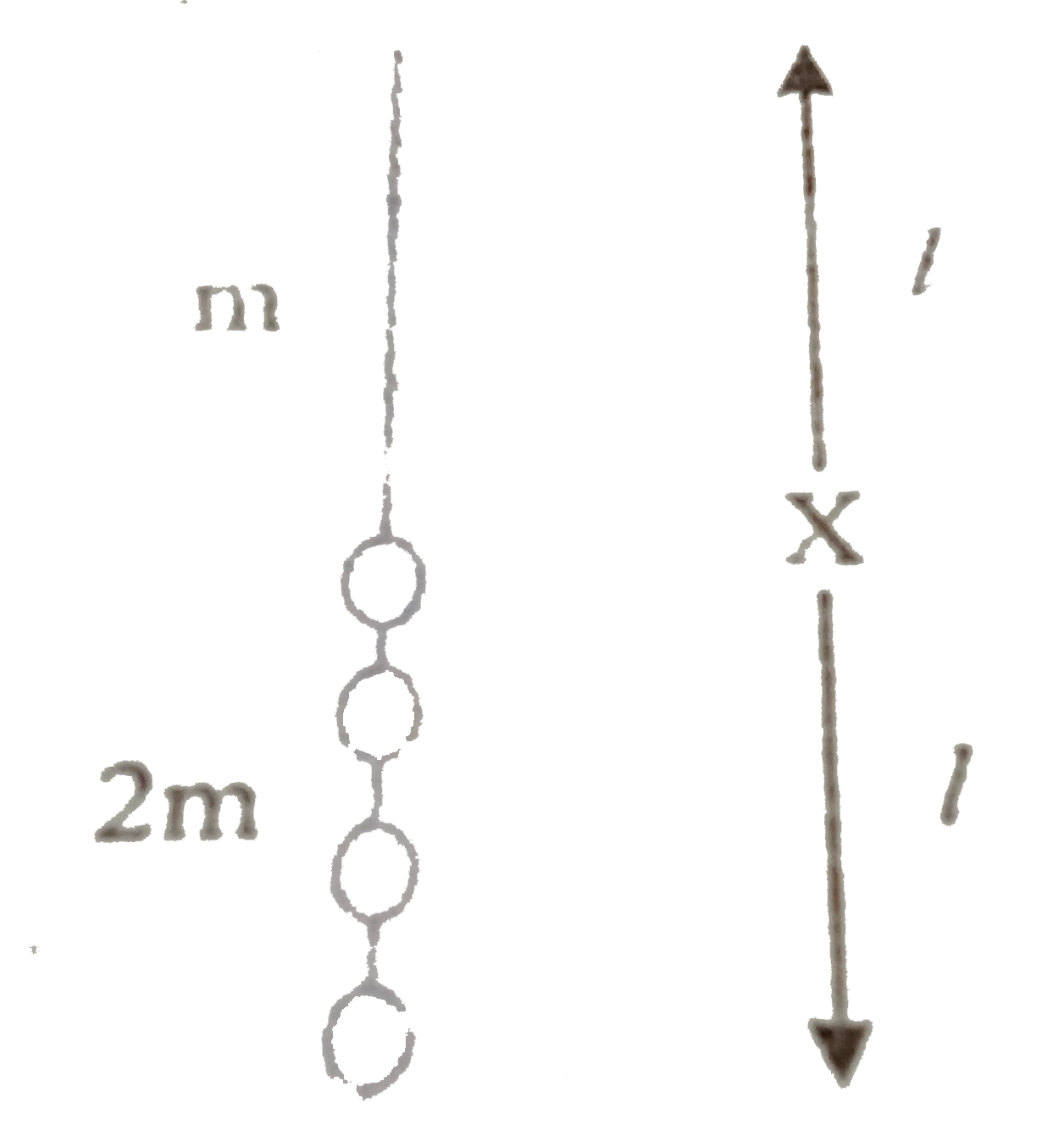 .
.
View SolutionFour identical particles each of mass m are arranged at the corners of a square of side length l. If the masses of the particles at the end of a side are doubled, the shift in the centre of mass of the system.
View Solution

