Three point masses are arranged as shown in the figure. Moment of inertia of the system about the axis OO' is
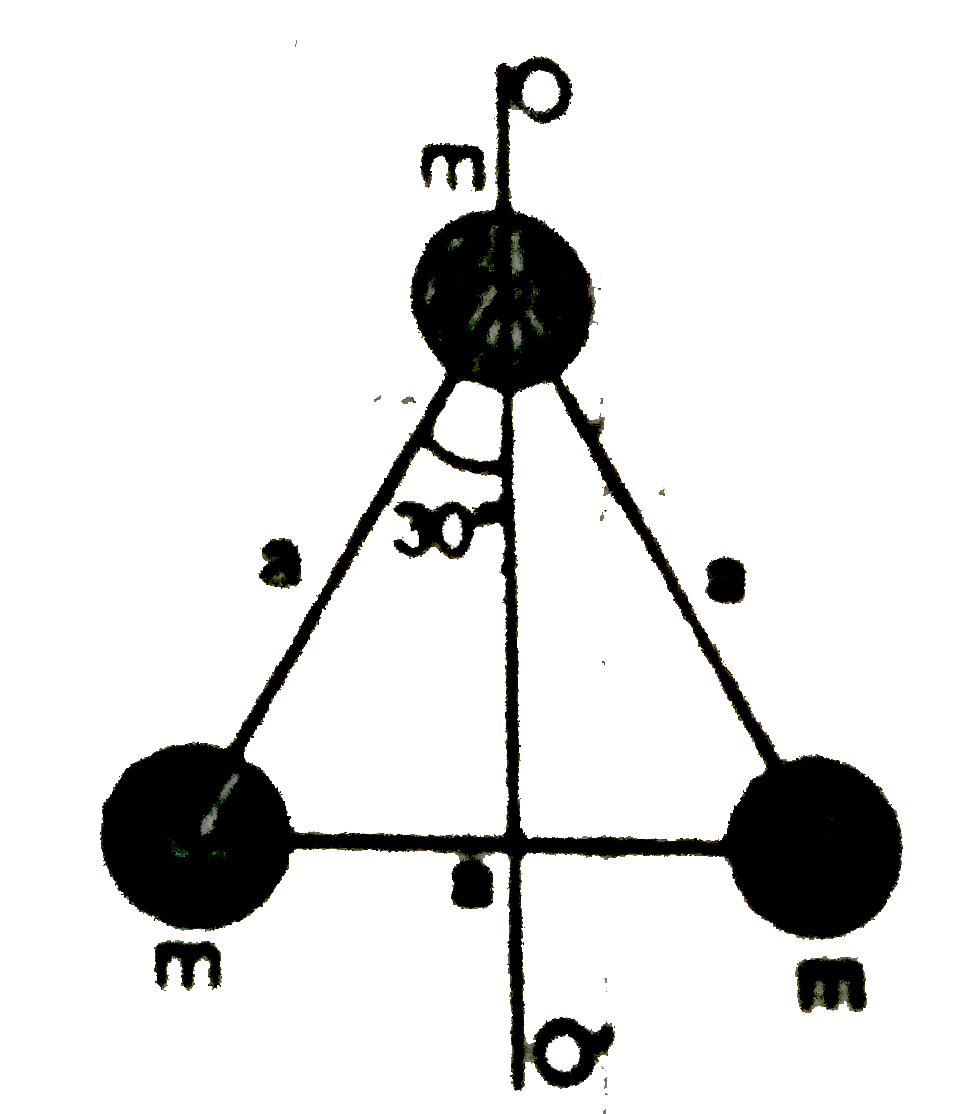
2ma2
ma22
ma2
none of these
The correct Answer is:B
I0,0=m(O)2+m(a2)2+m(a2)2=ma22
Topper's Solved these Questions
Similar Questions
The moment of inertia of a sphere about its diameter is I. Four such spheres are arranged as shown in figure. Find the moment of inertia of the system about the axis XX'. (radius of each sphere is 2R).
 View Solution
View SolutionFour rings each of mass M and radius R are arranged as shown in the figure. The moment of inertia of the system about YY' will be
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Three rings each of mass M and radius R are arranged as shown in the figure. The moment of inertia of the system about YY¢ will be
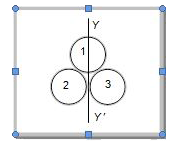 A3MR2B32MR2C5MR2D72MR2
A3MR2B32MR2C5MR2D72MR2 - Question 2 - Select One
Three rings each of mass M and radius R are arranged as shown in the figure . The moment of inertia of the system about AB is
(NAR_NEET_PHY_XI_P2_C07_E11_036_Q01.png" width="80%">A3Mr2B32MR2C5MR2D72MR2 - Question 3 - Select One
Three rings, each of mass P and radius Q are arranged as shown in the figure. The moment of inertia of the arrangement about YY' axis will be
 A72PQ2B27PQ2C25PQ2D52PQ2
A72PQ2B27PQ2C25PQ2D52PQ2
Three identical solid discs, each of mass M and radius R, are arranged as shown in figure. The moment of inertia of the system about an axis AB will be
 View Solution
View SolutionThee spheres each of mass M and radius R are placed in contact with each other as shown in the figure here. Then the moment of inertia of the system about the axis CC' is
 View Solution
View SolutionFour equal masses, m each are placed at the corners of a square of length (l) as shown in the figure. The moment of inertia of the system about an axis passing through A and parallel to DB would be:
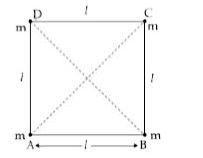 View Solution
View SolutionThree rings each of mass M and radius R are arranged according to the figure. The moment of inertia of this system about an axis XX' on its plane would be
 View Solution
View SolutionThree spheres, each mass M and radius R, are arranged as shown in the figure . The moment of inertia of the system will be
 View Solution
View Solution

