Three rings, each of mass m and radius r, are so placed that they touch each other. Find the moment of inertia about the axis as shown in Fig.

√65r
√56r
√67r
√76r
The correct Answer is:D
I=I1+I2+I3
I1=I2=32mr2
I3=mr22
∴I=I1+I2+I3=72mr2
moment of inertia=3mk4 where k is radius of gyration
3mk2=72mr2
⇒k=√76r

Topper's Solved these Questions
Similar Questions
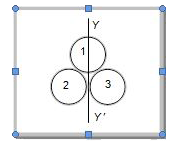
Three rings each of mass M and radius R are placed in contact with each other as shown . Then MI of the system about YY' axis is

View SolutionThee spheres each of mass M and radius R are placed in contact with each other as shown in the figure here. Then the moment of inertia of the system about the axis CC' is

View Solution
Knowledge Check
Three rings each of mass m and radius r are so placed that they touch each other. The radius of gyration of the system about the axis as shown in the figure is
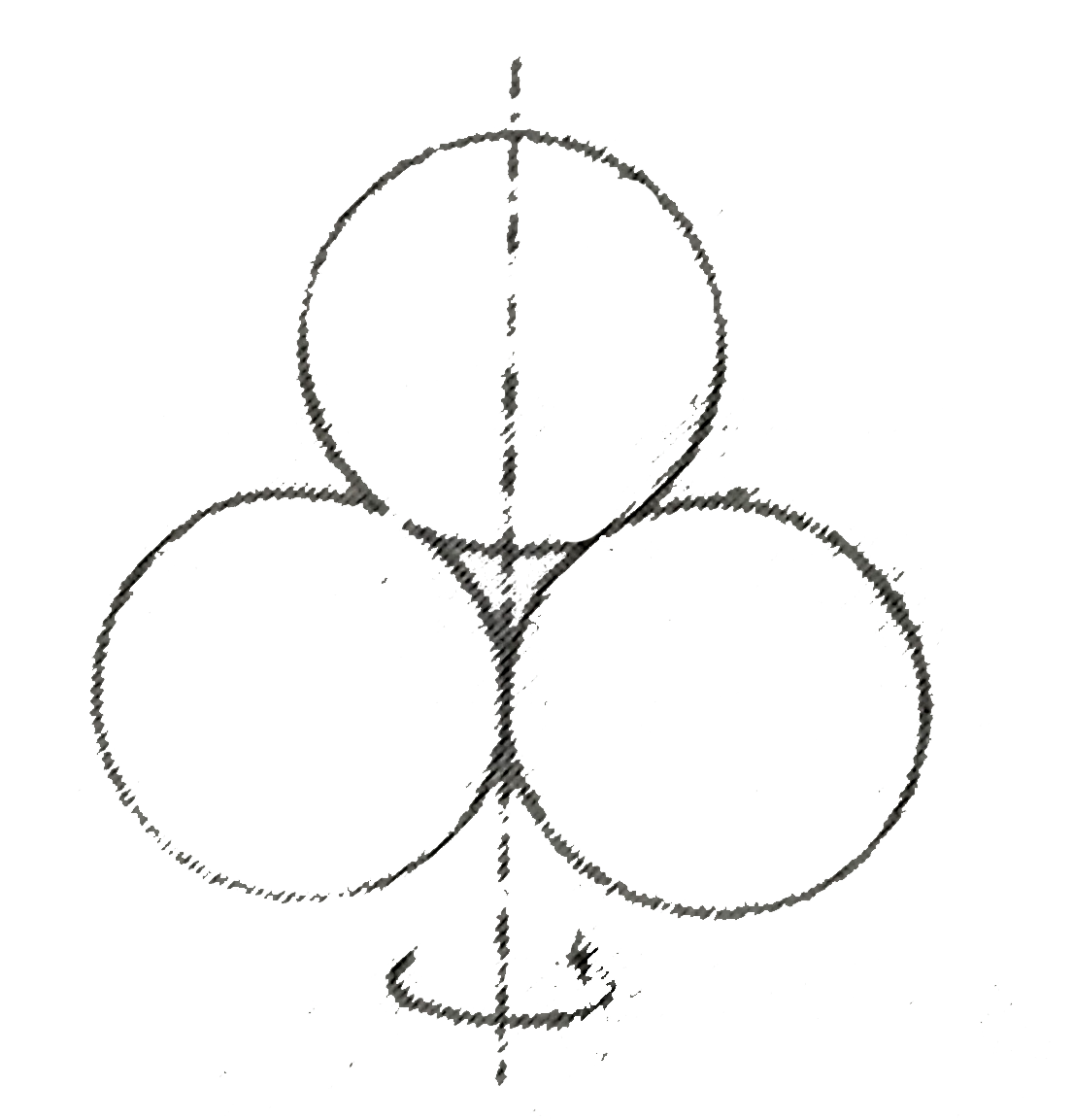 A√65rB√56rC√67rD√76r
A√65rB√56rC√67rD√76rThree rings each of mass M and radius R are arranged as shown in the figure. The moment of inertia of the system about YY¢ will be
 A3MR2B32MR2C5MR2D72MR2
A3MR2B32MR2C5MR2D72MR2Two identical concentric rings each of mass m and radius R are placed perpendicularly. What is the moment of inertia of the system about the axis of one of the rings ?
A3MR2B32MR2C14MR2D2MR2
Three rings each of mass M and radius R are arranged according to the figure. The moment of inertia of this system about an axis XX' on its plane would be

View SolutionFour rings each of mass M and radius R are arranged as shown in the figure. The moment of inertia of the system about YY' will be

View SolutionThree spheres, each mass M and radius R, are arranged as shown in the figure . The moment of inertia of the system will be

View SolutionThree rings, each of mass P and radius Q are arranged as shown in the figure. The moment of inertia of the arrangement about YY' axis will be

View SolutionTwo identical circular plates each of mass M and radius R are attached to each other with their planes ⊥r to each other. The moment of inertia of system about an axis passing through their centres and the point of contact is
View Solution
