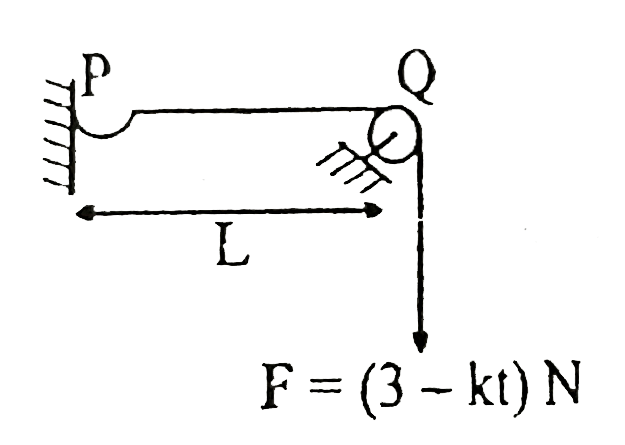
In the given figure a string of linear mass density $3 \times 10^{- 2}$ kg//m and length $L = 1$ m, is stretched by a froce $F = (3 - k t) N$ , where k is a constant and t is time in sec. At the time $t = 0$ , a pulse is generated at the end P of the string Find the value of k (in N//s) if the value of force becomes zero as the pulse reaches point Q.

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $20$

Time taken by pulse to reach from P to $Q (t_{0}) = \frac{F_{0}}{k}$ where $F_{0} = 3$
Now, $V = \sqrt{\frac{T}{m}} \Rightarrow \frac{d X}{d t} = \sqrt{\frac{F_{0} - k t}{m}}$
$∴ \underset{0}{\int^{L}} d X = \frac{1}{\sqrt{m}} \underset{0}{\int^{0}} {(F_{0} - k t)}^{1 / 2} d t$
$L = \frac{2}{3} k \sqrt{m} F_{0}^{3 / 2}$
$∴ k = \frac{2}{3 L} \sqrt{\frac{F_{0}^{3}}{m}} = \frac{2}{3 \times 1} \sqrt{\frac{3 \times 3 \times 3}{3 \times 10^{- 2}}} = \frac{2 \times 3}{3 \times 0.1} = 20$

|

Updated on:21/07/2023

Class 12 PHYSICS MASTER PRACTICE PROBLEM

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A tranverse wave propagating on a stretched string of linear density $3 \times 10^{- 4}$ kg per m is represented by the equation
$y = 0.2 sin (1.5 x + 60 t)$
Where , x is in metre and t is in second. The tension in the string (in newton) is
A0.24
B0.48
C1.2
D1.8
Question 2 - Select One
A $200 H z$ sinusoidal wave is travelling in the positive x-direction along a string with a linear mass density of $3.5 \times 10^{- 3} k g / m$ and a tension of $35 N$ . At time $t = 0$ , the point $x = 0$ , has maximum displacement in the positive y-direction. Next when this point has zero displacement, the slope of the string is $π / 20$ . Which of the following expression represent (s) the displacement of string as a function of $x$ (in metre) and $t$ (in second)
A $y = 0.025 cos (200 π t - 2 π x)$
B $y = 0.5 cos (200 π t - 2 π x)$
C $y = 0.025 cos (100 π t - 10 π x)$
D $y = 0.5 cos (100 π t - 10 π x)$
Question 3 - Select One
A string of length 10.0 m and mass 1.25kg stretched with a tension of 50N. If a transverse pulse is created at one end of the string, how long does it take to reach the other end ?
A0.5s
B1.0s
C1.5s
D2.0s

BANSAL-MASTER PRACTICE PROBLEM-Subjective

Home
Ask Doubt
Profile