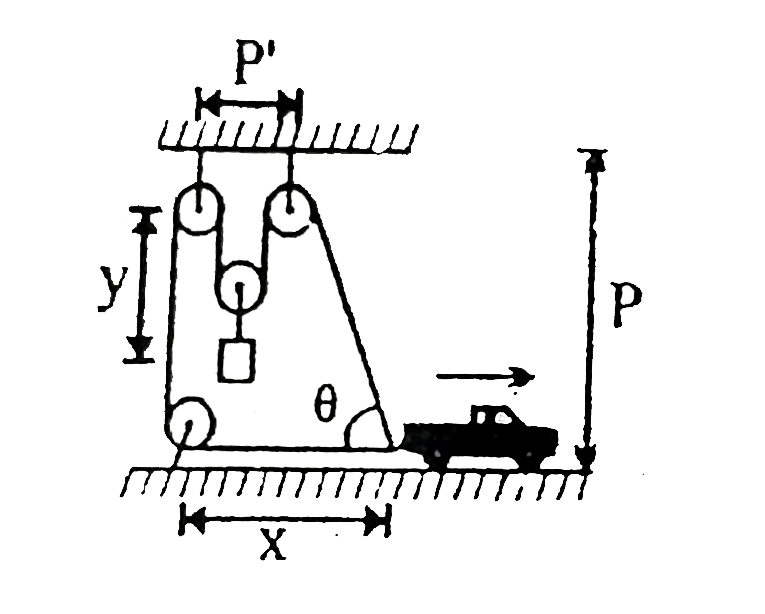
In fig. shown, the speed of the truck is v to the right. Find the speed with which the block is moving up at θ=60∘.

v
2v/3
3v/4
none
The correct Answer is:C
length of rope =const.
x+p+2y+√(x−p')2+p2=const
dxdt+0+2dydt+12(√(x−p')2+p2×2(x−p))dxdt=0
v−2v'+cos0v=0
2v'=v(1+cos0)
v'=v2(1+cos0)=v2(1+cos60∘)
v'=3v4Ans]
Topper's Solved these Questions
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Comphrehension
134 Videos
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Reasoning
75 Videos
- FLUID MECHANICSBOOK - BANSALCHAPTER - FLUID MECHANICSEXERCISE - PYQS AIEEE
10 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
Find the speed of the block after moving down by x
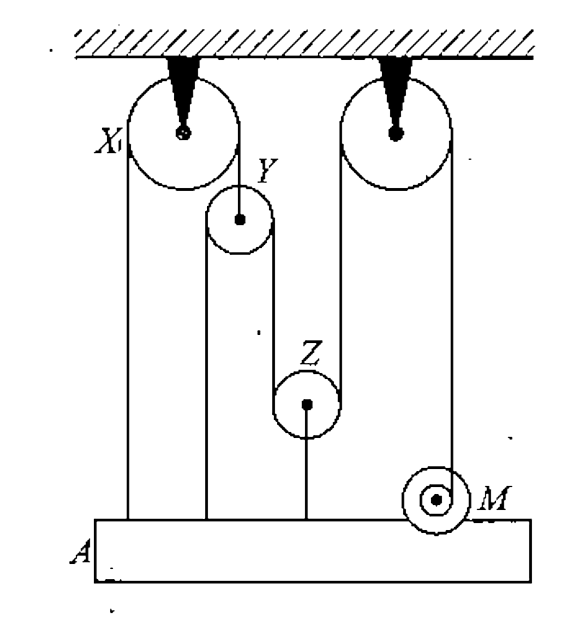
View SolutionConsider the situation of block pulley arrangement shown in figure-1.63. A plank is connected to three strings and an electric motor M is fitted on to it and a string is wound on it according to the arrangement shown in figure. Given that the string is winding on shaft of motor at a speed v. Find the speed with which the plank would be going up.
View Solution
Knowledge Check
truck is moving with a speed of 15 m/s. A car chasing this truck with a speed of 10 m/s fires a bullet at truck with muzzle velocity 90 km/h. The speed with which the bullet hit the truck is
A15 m/sB20 m/sC25 m/sD30 m/sThree blocks A, B and C each of mass m are placed on a surface as shown in the figure. Blocks B and C are initialyy at rest. Block A is moving to the right with speed v. It collides with block B and stricks to it. The A-B combination collides elastically with block C. Which of the following statement is (are) true about the velocity, of block B and C.
 AVelocity of the block C after collision is 2/3v towards rightBVelocity of the A−B combination after collision is v3 towards leftCVelocity of the A−B combination after collision is 23v towards leftDVelocity of the block C after collision is v3 towards right.
AVelocity of the block C after collision is 2/3v towards rightBVelocity of the A−B combination after collision is v3 towards leftCVelocity of the A−B combination after collision is 23v towards leftDVelocity of the block C after collision is v3 towards right.
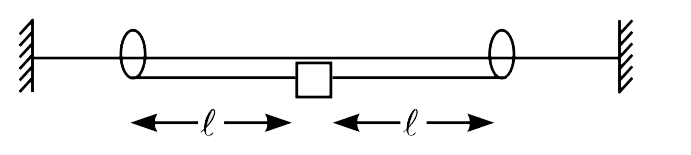
Two small rings each of mass ‘m’ are connected to a block of same mass ‘m’ through inextensible light strings. Rings are constrained to move along a smooth horizontal rod. Initially system is held at rest (as shown in figure) with the strings just taut. Length of each string is ‘l’. The system is released from the position shown. Find the speed of the block (v) and speed of the rings (u) when the strings make an angle of theta=60^(@)withvertical.(Takeg = 10 m//s^2)
View SolutionIn the figure shown, the mass of the hanging block is m, while that of the black resting on the floor is 3m. The floor is horizontal and frictionless and all pulleys ideal. The system is initially held stationary with the inclined thread making an angle θ=30∘ with the horizontal. The blocks are now released from rest and allowed to move. the hanging block falls through a height (49.5) m before hitting the floor. it is found that the value of θ becomes 60∘, when the hanging block hits the floor. Find the speed with which the hanging block hits the floor.

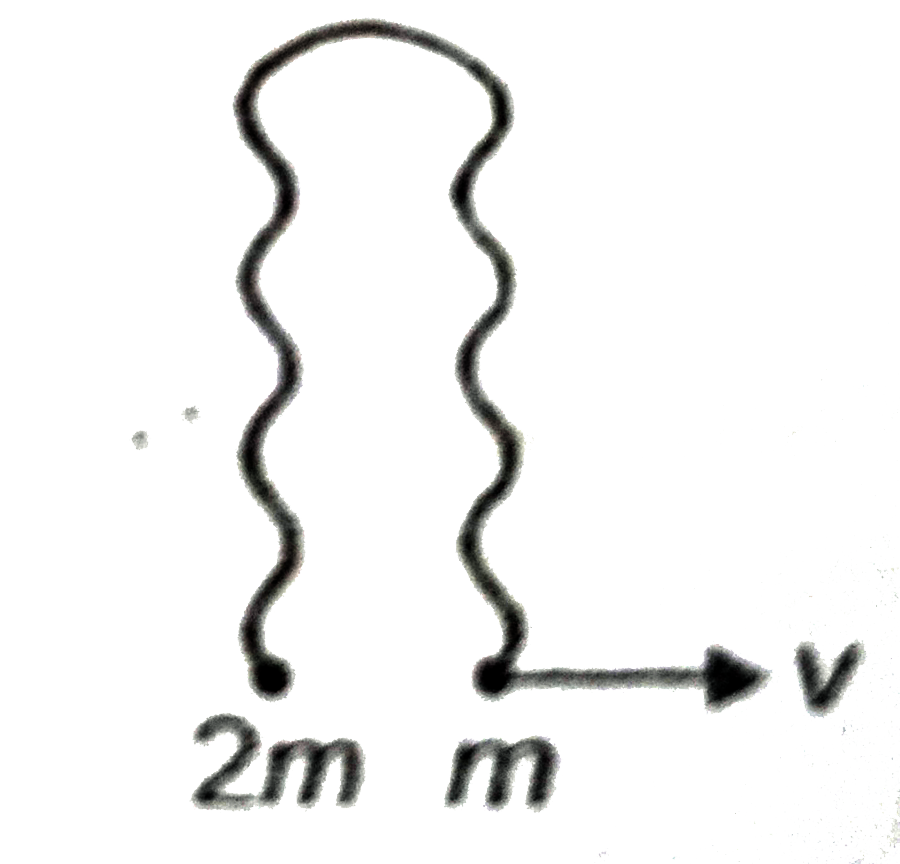
View SolutionTwo particles of a mass 2m and m are tied with an inextensible string the particle of mass m is given a speed V as shown in the figure. Find the speed with which the particle of mass 2m starts moving.
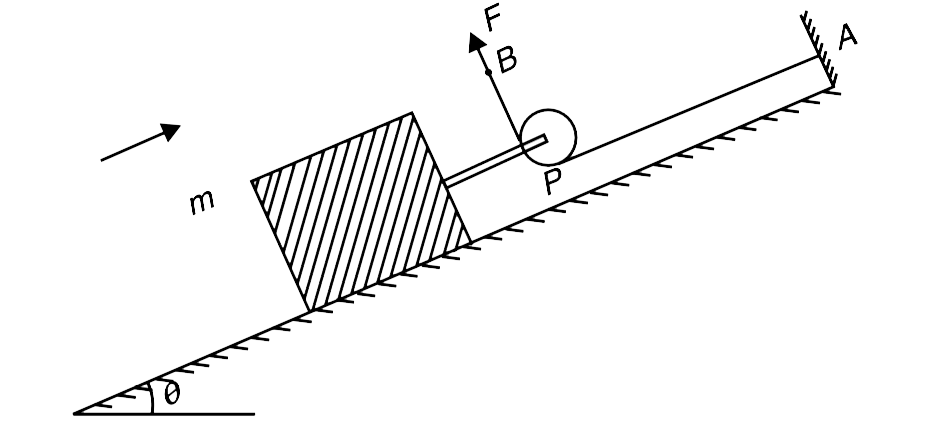
View SolutionIn the fig. shown, the pulley and string are mass less and the incline is frictionless. The segment AP of the string is parallel to the incline and the segment PB is perpendicular to the incline. End of the string is pulled with a constant force F.
(a) If the block is moving up the incline with acceleration while being in contact with the incline , then angle θ must be less than θ0. Find θ0
If θ=θ02 find the maximum acceleration with which the block can move up the plane without losing contact with the incline.
View SolutionA boy is standing on a truck moving with a constant velocity of 15m/s on the horizontal road. The boy throws a ball in such a way that it returns to the truck after the truck has moved 60m. Find the speed and the angle of projection (a) as seen by the truck and (b) as seen from the road.
View SolutionFind out the distance travelled by the block as shown in figure. If the initial speed of the block is v and μ is the friction coefficient between the surface of block and ground.
View Solution