A flexible pipe of length l connects two points A and B in space with an altitude difference h (Fig). A rope passed through the pipe is fixed at point A. Determine the initial acceleration a of the rope at the instant when it is released, neglecting the friction between the rope and the pipe walls.

Step by step video & image solution for A flexible pipe of length l connects two points A and B in space with an altitude difference h (Fig). A rope passed through the pipe is fixed at point A. Determine the initial acceleration a of the rope at the instant when it is released, neglecting the friction between the rope and the pipe walls. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A ring of mass m connecting freely two identical thin hoops of mass M each starts sliding down. The hoops move apart over a rough horizontal surface. Determine the acceleration a of the ring at the initial instant if ∠AO1O2=α (Fig), neglecting the friction between the ring and the hoops.

View SolutionTwo identical rings, each of mass M and radius R, are standing on a rough horizontal surface. The rings overlap such that the horizontal line passing through their centre makes an angle of θ=45∘ with the radius through their intersection point P. A small object of mass m is placed symmetrically on the rings at point P and released. Calculate the acceleration of the centre of the ring immediately after the release. There is no friction between the small object and the rings. The friction between the small object and the rings, and the friction between the rings and the ground is large enough to prevent slipping.
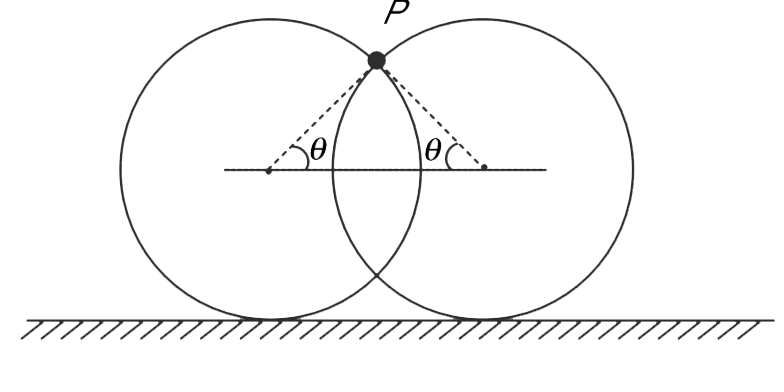
View Solution
Knowledge Check
A weightless inextensible rope rests on a stationary wedge forming an angle α with a horizontal One end of the rope is fixed to the wall to point A.A small load is attached to the rope at point B The wedge starts moving to the right with a constant acceleration a The acceleration of the load is given by
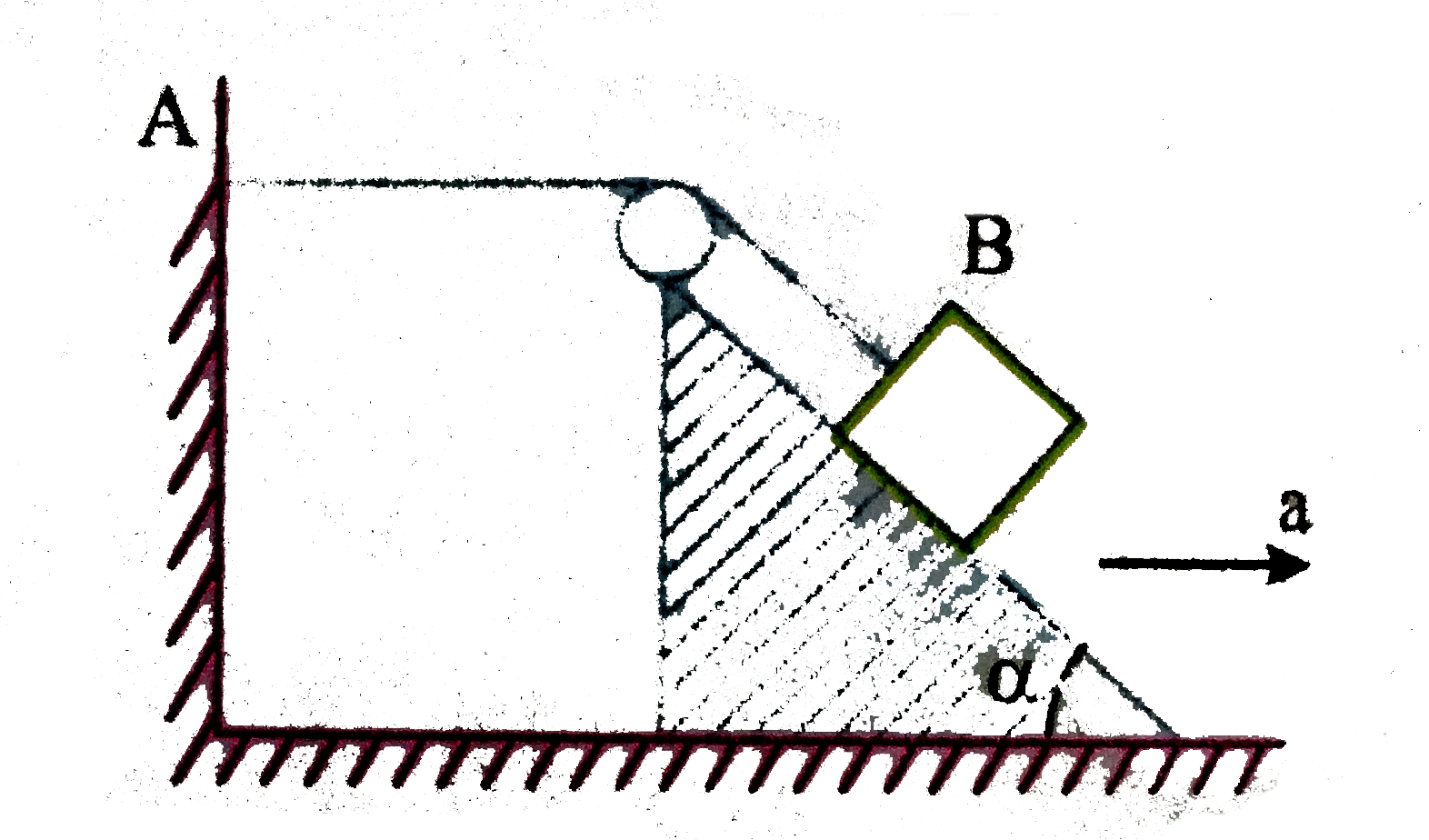 .AaB2asin(.α/2)CasinαDsin(.α/2)
.AaB2asin(.α/2)CasinαDsin(.α/2)A rope of mass 0.2 kg is connected at the same height of two opposite walls. It is allowed to hang under its own weight. At the contact point between the rope and the wall, the rope makes an angle θ=30%∘ with respect to horizontal. The tension in the rope at its midpoint between the walls is
A1.78 NB1.56 NC1.82 ND1.96 N
A man of mass M stands on a.box of mass m as shown in the Fig. 2E. l (a). A rope attached to 'the box and passing over an overhead pulley allows the man to raise himself and the box by , pulling the rope downward.
(i) With what minimum force should the ' man pull the rope so as to prevent himself , from falling down.
(ii) If the man pulls the rope with a force F greater than the minimum force, then determine the acceleration of the (man + box) system.
(iii) Determine. the normal reaction between the man and the trolley.
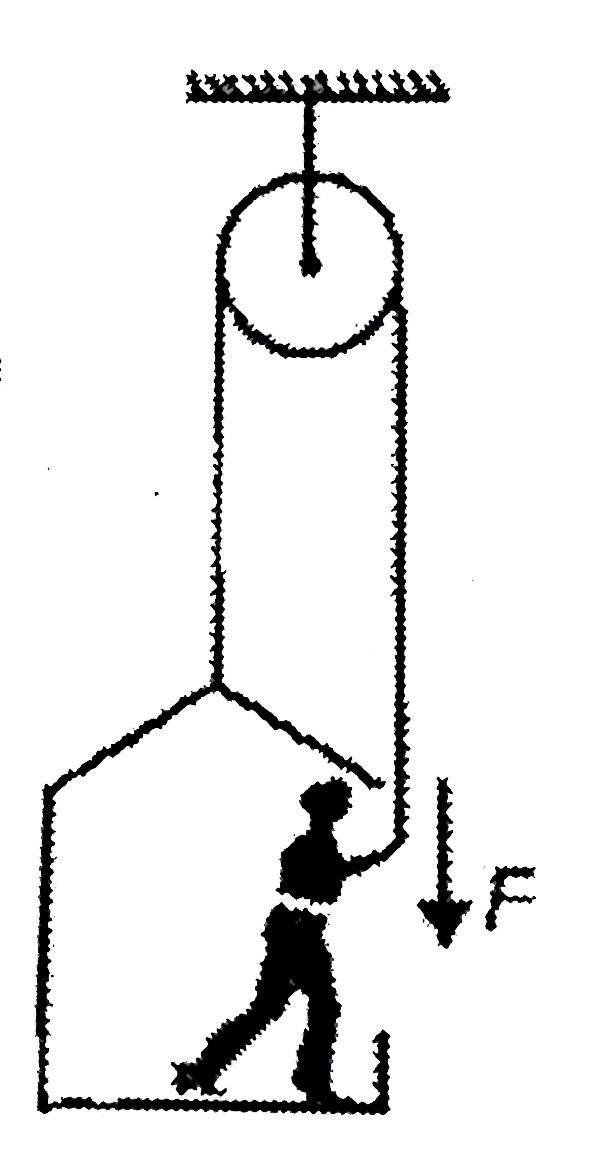
View SolutionTwo blocks A and B of equal masses are attached to a string passing over a smooth pulley fixed to a wedge as shown in figure. Find the magnitude of acceleration of centre of mass of the two blocks when they are released from rest. Neglect friction.

View SolutionA rope of length L and mass per unit length λ passes over a disc shaped pulley of mass M and radius R. The rope hangs on both sides of the pulley and the length of larger hanging part is l. The pulley can rotate about a horizontal axis passing through its centre. The system is released from rest and it begins to move. The pulley has no friction at its axle and the rope has large enough friction to prevent it from slipping on the pulley.
(a) Find the acceleration of the rope immediately after it is released.
(b) Find the horizontal component of the force applied by the axle on the pulley immediately after the system is released
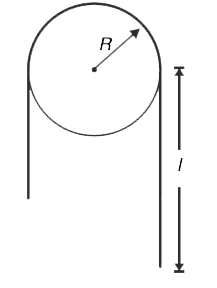
View SolutionOne end of a horizontal uniform beam of weight W and length L is hinged on a vertical wall at point O and its other end is supported by a light inextensible rope. The other end of the rope is fixed at point Q at a height L above the hinge at point O. A block of weight αW is attached at the point Q at a height L above the hinge at point O. A block of weight αW is attached at the point P of the beam as shown in the figure. The rope can sustain a maximum tension of 2(√2)W. Which of the following statements is/are correct?
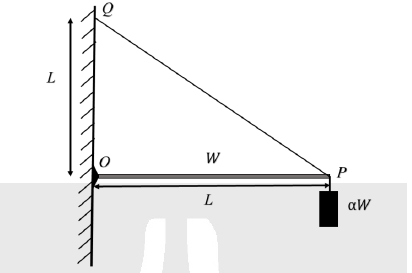
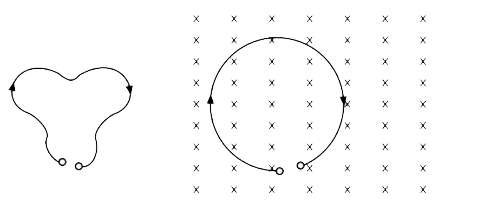
View SolutionA thin flexible wire of length L is connected to two adjacent fixed points and carries a current I in the clockwise direction, as shown in the figure. When the system is put in a uniform magnetic field of strength B going into the plane of the paper, the wire takes the shape of a circle. The tension in the wire is :
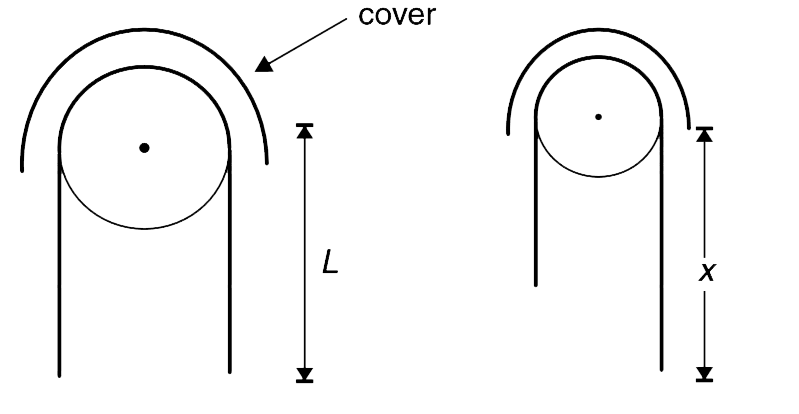
View SolutionA heavy rope of mass m and length 2L is hanged on a smooth little peg with equal lengths on two sides of the peg. Right part of the rope is pulled a little longer and released. The rope begins to slide under the action of gravity. There is a smooth cover on the peg (so that the rope passes through the narrow channel formed between the peg and the cover) to prevent the rope from whiplashing.
(a) Calculate the speed of the rope as a function of its length (x) on the right side.
(b) Differentiate the expression obtained in (a) to find the acceleration of the rope as a function of x.
(c) Write the rate of change of momentum of the rope as a function of x. Take downward direction as positive
(d) Find the force applied by the rope on the peg as a function of x.
(e) For what value of x, the force found in (d) becomes zero? What will happen if there is no cover around the peg ?
View Solution

