A long smooth cylindrical pipe of radius r is tilted at an angle α to the horizotal (Fig). A small body at point A is pushed upwards along the inner surface of the pipe so that the direction of its initial velocity forms an angle φ with generatrix AB. Determine the minimum initial velocity v0 at which the body starts moving upwards without being separated from the surface of the pipe.

Step by step video & image solution for A long smooth cylindrical pipe of radius r is tilted at an angle alpha to the horizotal (Fig). A small body at point A is pushed upwards along the inner surface of the pipe so that the direction of its initial velocity forms an angle varphi with generatrix AB. Determine the minimum initial velocity v_(0) at which the body starts moving upwards without being separated from the surface of the pipe. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
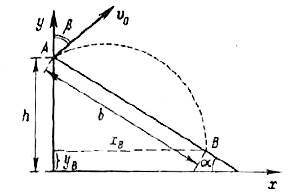
The surface of a hill is inclined at an angle α to the horizontal (Fig.). A stone is thrown from the summit of the hill at an initial speed v0 at an angle β to the vertical. How far from the summit will the stone strike the ground?
 View Solution
View SolutionA body is projected upwards. What is its initial velocity at maximum height?
View Solution
Knowledge Check
- Question 1 - Select One
A body is projected vertically upward from the surface of the earth, then the velocity-time graph is:-
A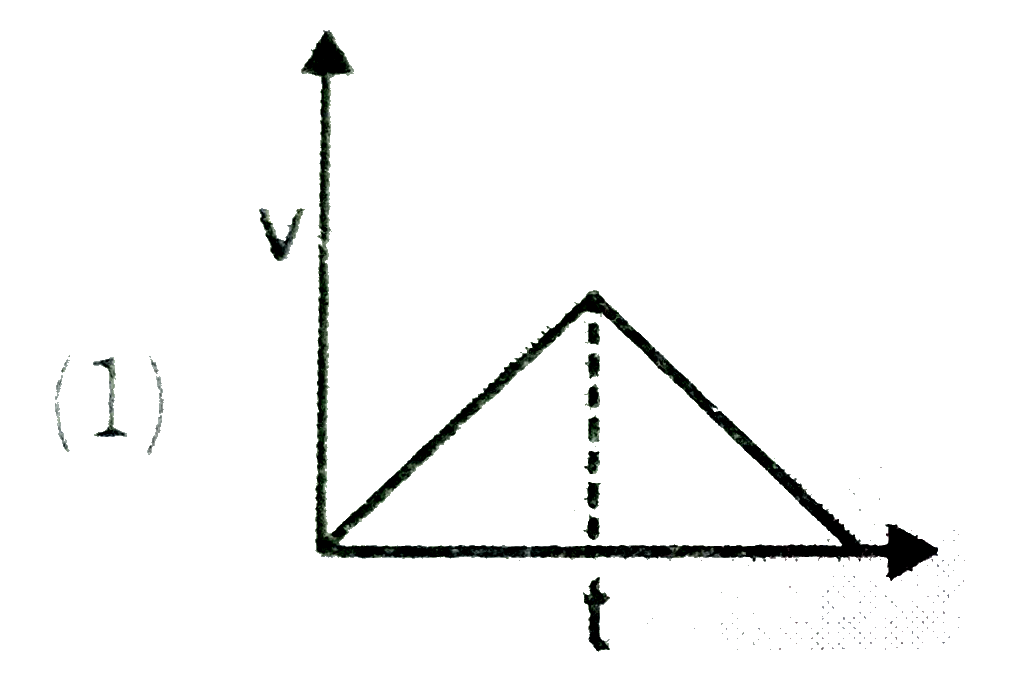 B
B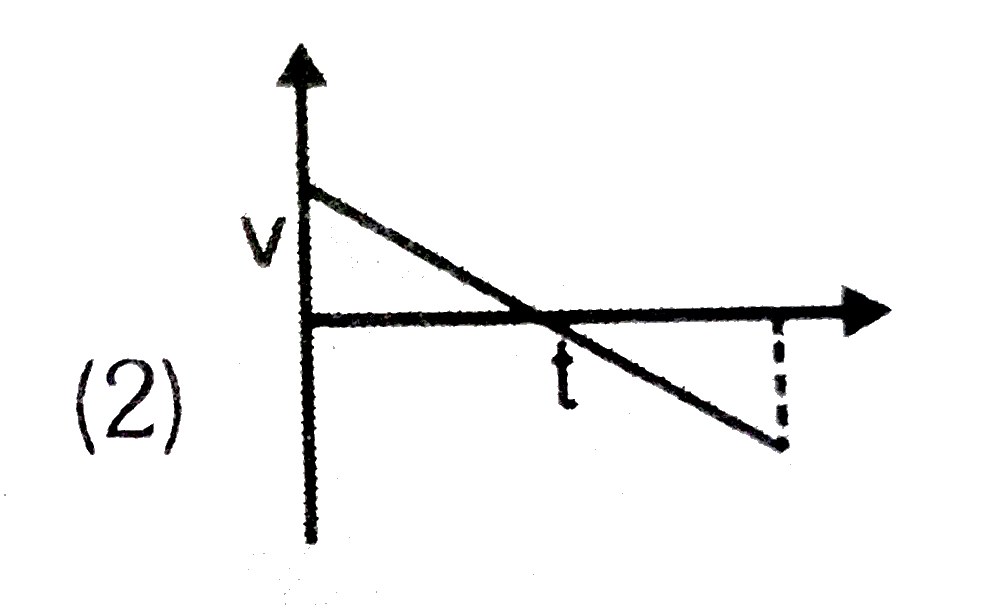 C
C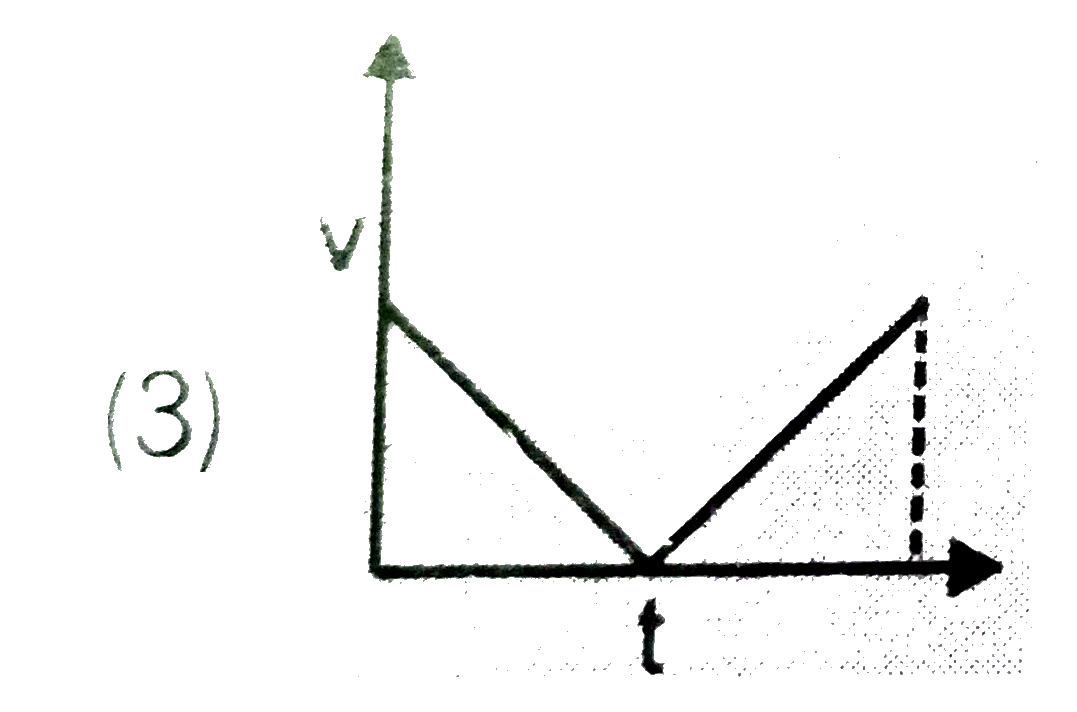 D
D
- Question 2 - Select One
A particle is project d from point A with velocity u at an angle α with horizontal. In its parabolic path, at point P the particle is moving at right angles to its initial direction of projection. Its velocity at P is:
AutanαBucotαCucosαDucosecα - Question 3 - Select One or More
A particle is projected from a point O with a velocity u at an angle α (upwards) to the horizontal. At a certain point P it moves at right angles to its initial direction. It follows that:
AOP makes an angle tan−1(u/2g) to the horizontalBthe distance of P from O is u/(2gsinα).Cthe time of flight from O to P is u/(gsinα)Dthe velocity of the particle at P is u cot α
A ball of radius 1 cm is put into a cylindrical pipe so that it fits inside the pipe. If the length of the pipe is 14 m, what is the surface area of the pipe?
View SolutionThe escape velocity of a body projected vertically upwards from the surface of the earth is v.If the body is projected in a direction making an angle θ with the vertical, the vetical, the escape velocity would be
View SolutionA particle is projected from a point P with a velocity v at an angle θ with horizontal. At a certain point Q it moves at right angles to its initial direction. Then
View SolutionA body falls freely from a height of 50 m. Simultaneously, another body is thrown from the surface of earth with a certain initial velocity. The two bodies meet at a height of 10 m. What is the initial velocity of the second body ?
View SolutionA body is imparted a velocity v from the surface of the earth. If v0 is orbital velocity and ve be the escape velocity then for :
View Solution

