A heavy ball of mass m is tied to a weightless thread of length 1. The

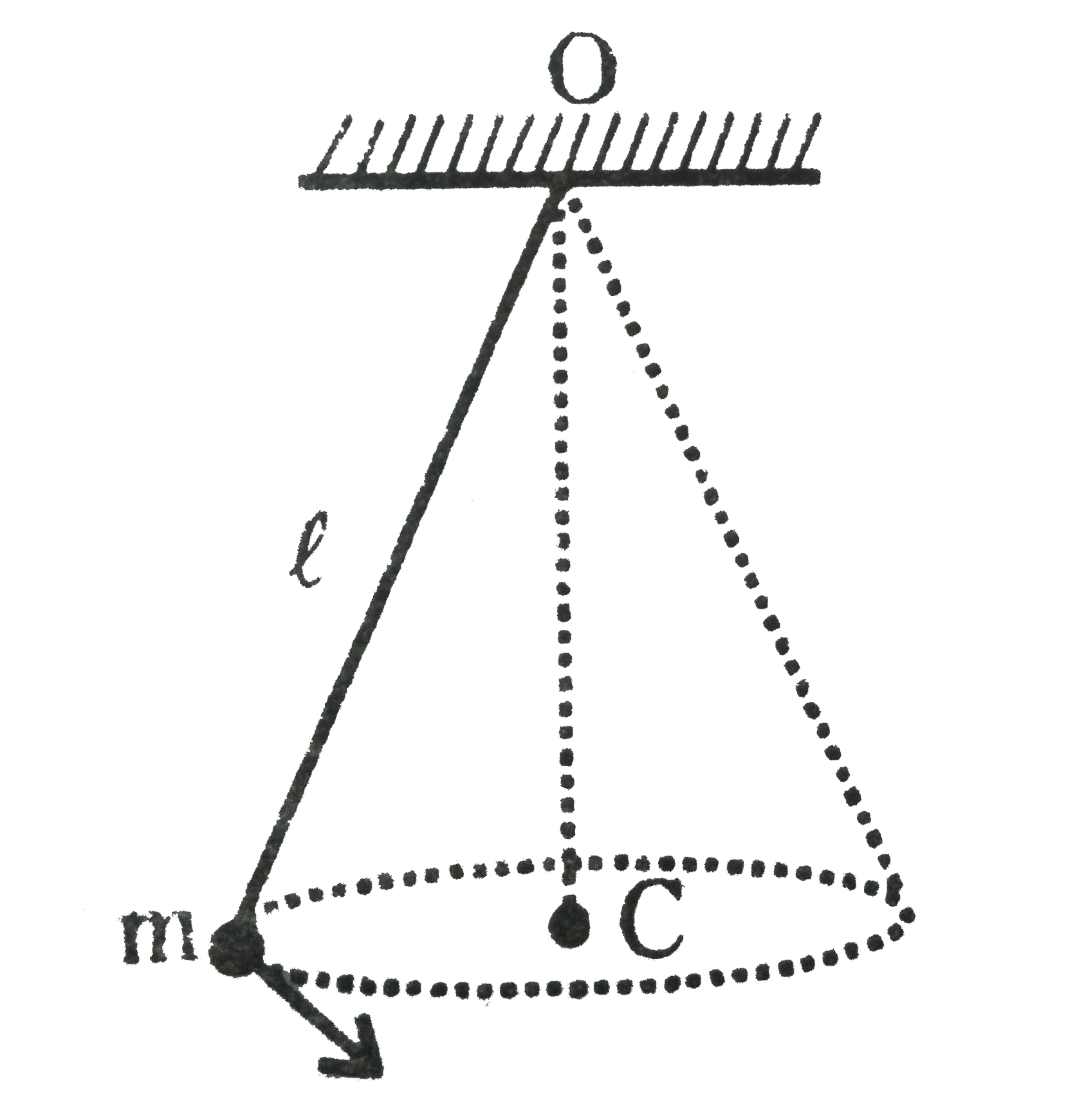
A small ball of mass $m$ suspended from the celling at a point $O$ by a thread of length $l$ moves along a horizontal circle with a constant angular velocity $ω$ .
.
Alinear momentum of system (ball + rod) is conserved
Bangular momentum about C is conserved
Ckinetic energy of system (ball + rod) before the collision is equal to kinetic energy of system just after the collision
Dlinear momentum of ball is conserved
A solid rubber ball orf density $d$ and radius $R$ falls vertically through air. Assume that the air resistance acting on the ball is $F = K R V$ where K is constant and V is its velocity. Because of this air resistance the ball attains a constant velocity called terminal velocity $v_{T}$ after some time. Then $V_{T}$
A $\frac{4 π R^{2} d g}{3 K}$
B $\frac{3 K}{4 π R^{2} d g}$
C $\frac{4}{3} \frac{π r^{3} d g}{K}$
D $π r d g k$

A small ball of mass $m$ suspended from the celling at a point $O$ by a thread of length $l$ moves along a horizontal circle with a constant angular velocity $ω$ .
.