f(x)=x2. Find f−1.
To find the inverse of the function f(x)=x2, we will follow these steps:
Step 1: Replace f(x) with y
We start by rewriting the function:
y=x2
Step 2: Swap x and y
Next, we swap x and y to find the inverse:
x=y2
Step 3: Solve for y
Now, we need to isolate y. To do this, we take the square root of both sides:
y=±√x
Step 4: Write the inverse function
This gives us:
f−1(x)=±√x
Step 5: Determine if the inverse is a function
However, we must check if this inverse is a valid function. A function must assign exactly one output for each input. Since f−1(x)=±√x yields two values (positive and negative) for each positive x, it does not satisfy the definition of a function.
Conclusion
Thus, we conclude that the inverse function f−1(x) does not exist in the context of a function because it does not provide a unique output for each input.
---
We start by rewriting the function:
y=x2
Next, we swap x and y to find the inverse:
x=y2
Now, we need to isolate y. To do this, we take the square root of both sides:
y=±√x
This gives us:
f−1(x)=±√x
However, we must check if this inverse is a valid function. A function must assign exactly one output for each input. Since f−1(x)=±√x yields two values (positive and negative) for each positive x, it does not satisfy the definition of a function.
Thus, we conclude that the inverse function f−1(x) does not exist in the context of a function because it does not provide a unique output for each input.
Topper's Solved these Questions
Similar Questions
If {(3,2),(4,2),(3,1),(7,1),(2,3)} is to be a function, which one of the following must be removed from the set?
View SolutionIf xa⋅(xa+1)a⋅(xa)1−a=xk, then k=
View Solution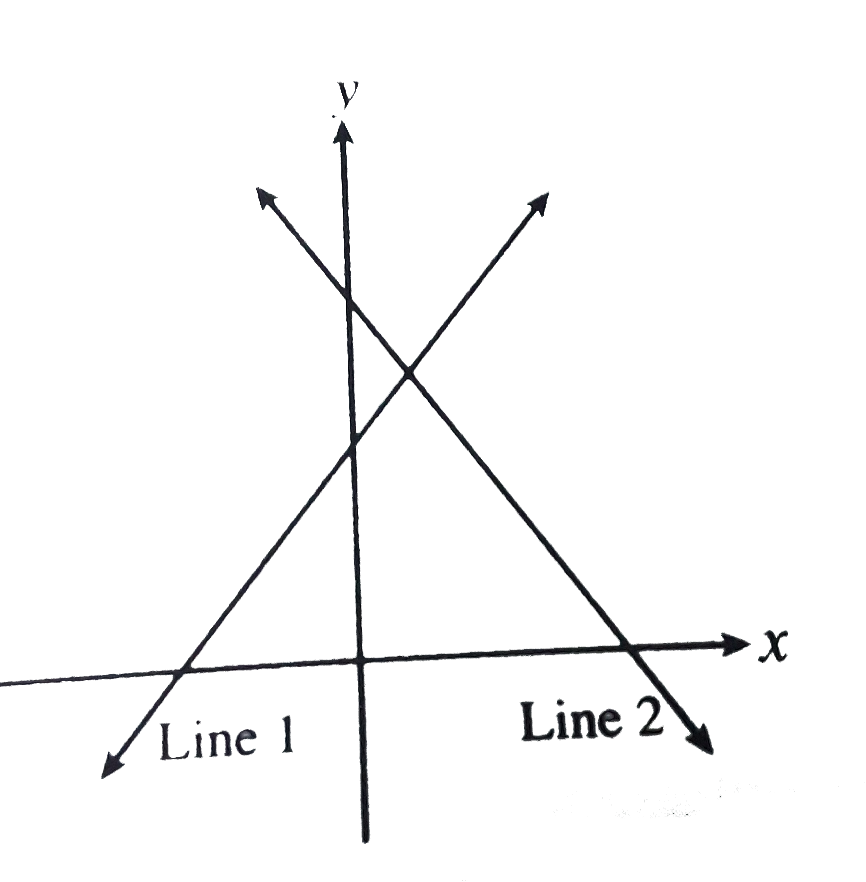
Consider two lines in the xy-plane , as shown above. If line 1 has equation y=m1x+b1, and line 2 has equation y=m2x+b2. Which is a true statement ?
View SolutionFind f(f(x)) if f(x)=x+1;0<=x<=1 and 1-x;1
View Solutionf(x)+f(1-x)=2 then find f((1)/(2))=
View SolutionIf f′(x)=x−1x2 and f(1)=12 , find f(x) .
View SolutionIf f(x)=x+1x−1,x≠1, find f(f(f(f(2)))))
View SolutionFind f(f(f(f(f(2)))))) if f(x)=x+1x−1,x≠1
View SolutionIf f′(x)=x−1x2 and f(1)=12 , find f(x) .
View SolutionIf f′(x)=x−1x2 and f(1)=12 , find f(x) .
View SolutionIf f'(x)=1−4x2 and f(1)=6 then find f(x) and f(2).
View SolutionIf f'(x)=x−1x2 and f(1)=12 then find f(x).
View SolutionIf f(x)=x+1x−1 then the value of f(f(f(x))) is :
View SolutionFind f(f(f(f(f(2)))))) if f(x)=x+1x−1,x≠1
View SolutionIf f(x)f(y) + 2 = f(x) + f(y) + f(xy) and f(1) = 2, f'(1) = 2, then find f(x).
View SolutionIf f(x) = x2−5|x|+2, find f(0),f(1),f(-1)
View Solution

