. Is the inverse of f?
To determine if g(x)=x−23 is the inverse of f(x)=3x+2, we will use the property of inverse functions. The property states that if g is the inverse of f, then:
g(f(x))=xandf(g(x))=x
Step 1: Calculate g(f(x))
First, we will substitute f(x) into g(x):
f(x)=3x+2
Now, substitute f(x) into g(x):
g(f(x))=g(3x+2)=(3x+2)−23
Step 2: Simplify g(f(x))
Now, simplify the expression:
g(f(x))=3x+2−23=3x3=x
Step 3: Calculate f(g(x))
Next, we will substitute g(x) into f(x):
g(x)=x−23
Now, substitute g(x) into f(x):
f(g(x))=f(x−23)=3(x−23)+2
Step 4: Simplify f(g(x))
Now, simplify the expression:
f(g(x))=3⋅x−23+2=(x−2)+2=x
Conclusion
Since both g(f(x))=x and f(g(x))=x, we can conclude that g(x) is indeed the inverse of f(x).
Final Answer
Yes, g(x)=x−23 is the inverse of f(x)=3x+2.
---
Topper's Solved these Questions
Similar Questions
If {(3,2),(4,2),(3,1),(7,1),(2,3)} is to be a function, which one of the following must be removed from the set?
View SolutionIf xa⋅(xa+1)a⋅(xa)1−a=xk, then k=
View Solution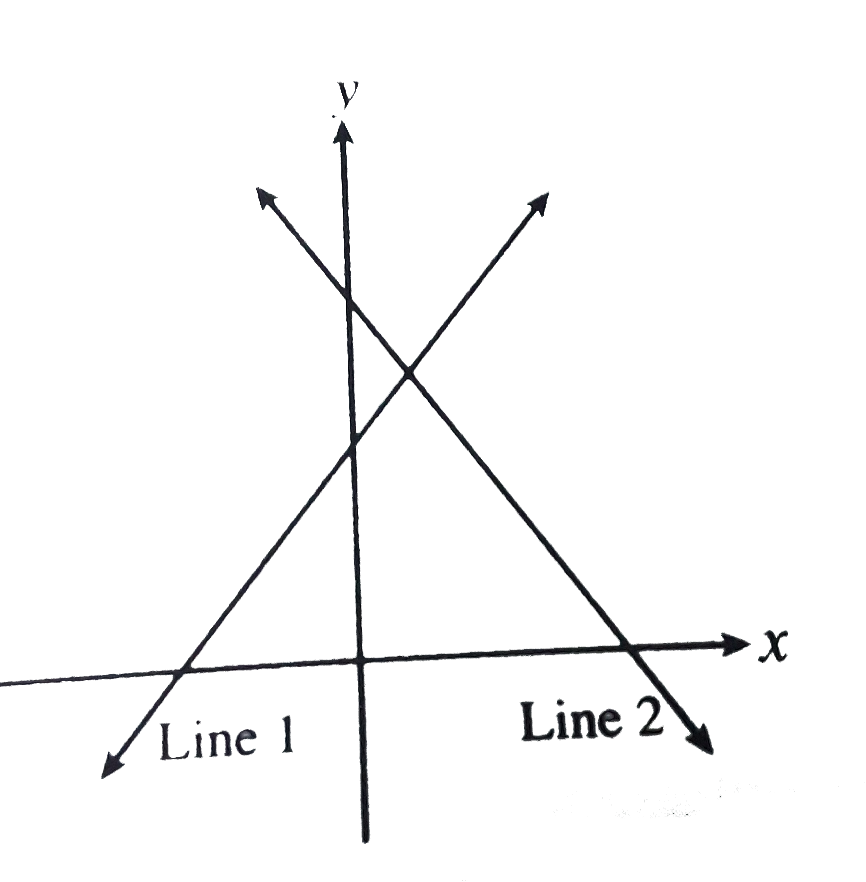
Consider two lines in the xy-plane , as shown above. If line 1 has equation y=m1x+b1, and line 2 has equation y=m2x+b2. Which is a true statement ?
View Solutionf'(x)>=g'(x), if f(x)=5-3x+(5)/(2)x^(2)-(x^(3))/(3),g(x)=3x-7
View SolutionLet f(x)=x^(2)-4x-3,x>2 and let g be the inverse of f. Find the value of g', where f(x)=2
View SolutionLet f(x)=x+cosx+2andg(x) be the inverse function of f(x), then g'(3) equals to ........ .
View SolutionIf f(x)=2x3 and g(x)=3x, what is the value of g(f(−2))−f(g(−2)) ?
View SolutionIf g(x)=3x+2andg(f(x))=x, then f(2)=
View SolutionIf f(x)=x3+3x+1andg(x) is the inverse function of f(x), then the value of g'(5) is equal to
View SolutionIf g(x)=x3+x−2 and g(f(x))=x3+3x2+4x then f(1)+f(2) is equal to ________
View SolutionIf f(x)=3x+1 and g(x)=x3+2 then (f+gf⋅g)(0) is:
View SolutionLet f(x)=x3+3x+2 and g(x) is inverse function of f(x) then the value of g'(6) is
View Solutionयदि f:N→I और g:I→Q इस प्रकार से परिभाषित है की f(x)=3x तथा g(x)=x+23 हो, तो gof:N→Qज्ञात कीजिए
View SolutionIf f(g(x)) = x and g(f(x)) = x then g(x) is the inverse of f(x).(g'(x))f'(x)=1⇒g'(f(x))=1f'(x)
If f(x) = x3+x2+logexandg is inverse of f then 6'g(6) is equal to
View SolutionLet f(x)=x+cosx+2andg(x) be the inverse function of f(x), then g'(3) equals to ........ .
View Solution

