A source of laser (S), a receiver (R) and a fixed mir- ror (F) – all lie on an arc of a circle of radius R=0.5km. The distance between the source and the receiver is d=0.5m. At the centre of the circle there is a small mirror M which is rotating with angular speed ω (see figure). Find smallest value of ω is if it is seen that the source shoots a laser pulse which gets reflected at M, then gets reflected at F and finally gets reflected at M to be received by the receiver.
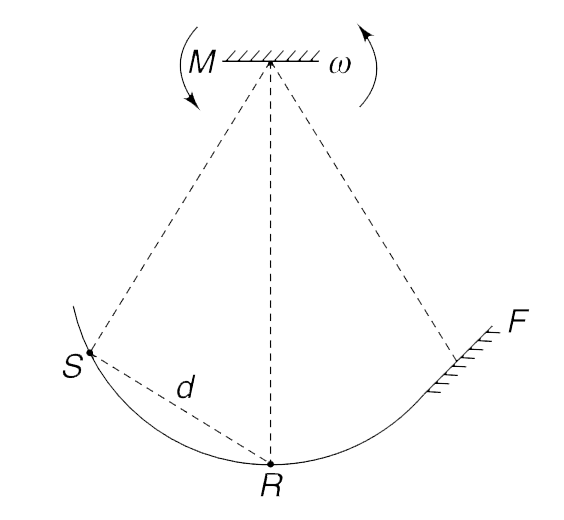
The correct Answer is:150rads−1
Step by step video, text & image solution for A source of laser (S), a receiver (R) and a fixed mir- ror (F) – all lie on an arc of a circle of radius R = 0.5 km. The distance between the source and the receiver is d = 0.5 m. At the centre of the circle there is a small mirror M which is rotating with angular speed omega (see figure). Find smallest value of omega is if it is seen that the source shoots a laser pulse which gets reflected at M, then gets reflected at F and finally gets reflected at M to be received by the receiver. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ARIHANTCHAPTER - GEOMETRICAL OPTICSEXERCISE - Level 2
62 Videos
- GEOMETRICAL OPTICSBOOK - ARIHANTCHAPTER - GEOMETRICAL OPTICSEXERCISE - Level 3
9 Videos
- ELECTROSTATICSBOOK - ARIHANTCHAPTER - ELECTROSTATICSEXERCISE - Level 3
59 Videos
- MAGNETIC EFFECT OF CURRENTBOOK - ARIHANTCHAPTER - MAGNETIC EFFECT OF CURRENTEXERCISE - Magnetic effect of Current
45 Videos
Similar Questions
A bead of mass m stays at point P (a,b) on a wire bent in the shape of a parabola y=4Cx2 and rotating with angular speed ω (see figure ) . The value of ω is (neglect friction),
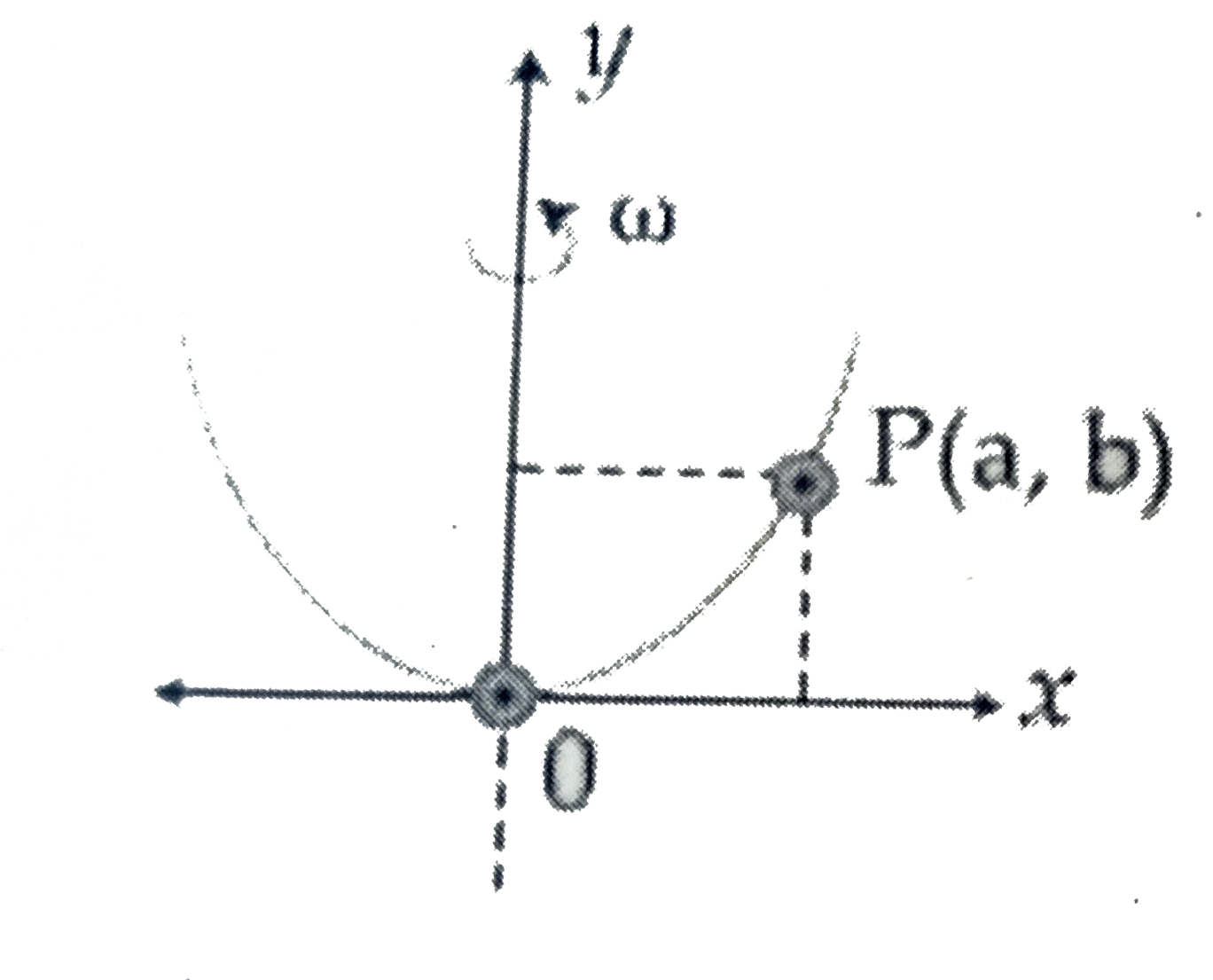
View SolutionFind the angular momentum of a particle of mass m describing a circle of radius r with angular speed ω.
View Solution
Knowledge Check
A helium nucleus makes a full rotation in a circle of radius 0.8 m in 2 s. The value of the magnetic field B at the centre of the circle will be
A1019μ0B10−19μ0C2×10−10μ0D2×1010μ0R and r are the radius of two circles (R>r). If the distance between the centre of the two circles be d, then length of common tangent of two circles is
A√d2−(R−r)2B√(R−r)2−d2C√R2−d2D√r2−d2A helium nucleus makes full rotation in a circle of radius 0.8 m in 2.5 seconds. The value of magnetic field B at the centre of the circle will be
A3.1π×10−26TB2π×10−26TC4π×10−25TD2π×10−25T
A disc of mass m and radius R rotating with angular speed ω0 is placed on a rough surface (co-officient of friction =μ). Then

View SolutionA wheel of moment of inertial I and radius R is rotating about its axis at an angular speed ω. It picks up a stationary particle of mass m at its edge. Find the new angular speed of the wheel.
View SolutionA particle moves along a circle of radius R with a constant angular speed ω. Its displacement (only magnitude) in time t will be
View SolutionA particle moves along a circle of radius R with a constant angular speed ω . Its displacement (only magnitude) in time t will be
View SolutionA circular disc of mass M and radius R is rotating with angular velocity ω . If two small spheres each of mass m are gently attached to two diametrically opposite points on the edge of the disc, then the new angular velocity of the disc will be
View Solution