A large number of particles are moving each with speed v having directions of motion randomly distributed. What is the average relative velocity between any two particles averaged over all the pairs?
v
(π/4)v
(4/π)v
Zero
The correct Answer is:C
Relative velocityt, vr=|→v1−→v2| where v1=v2=v
If angle between them be θ, then vr=√v2+v2−2v2cosθ=√2v2(1−cosθ)=2vsin(θ2)
Hence, average relative velocity →vr=2π∫02v sinθ2dθ2π∫0dθ=4vπ
Topper's Solved these Questions
- KINEMATICSBOOK - ALLENCHAPTER - KINEMATICSEXERCISE - EXERCISE-01
55 Videos
- KINEMATICSBOOK - ALLENCHAPTER - KINEMATICSEXERCISE - EXERCISE-02
57 Videos
- ERROR AND MEASUREMENTBOOK - ALLENCHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)
22 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
Similar Questions
Consider a collection of a large number of particles each with speed v. The direction of velocity is randomly distributed in the collection. Show that the magnitude of the relative velocity between a pair of particles averaged over all the pairs in the collection is greater than v.
View SolutionA particle is moving with a constant speed v in a circle. What is the magnitude of average velocity after half rotation?
View Solution
Knowledge Check
Consider a collection of a large number of particles each with speed v in a plane.The direction of velocity is randomly distributed in the collection.The magnitude of the average relative velocity of a particle with velocities of all other particles is
A>vB<vC=vDnone of theseIn maxwell's speed distribution curve, for N2 gas, the average of |relative velocity| between two molecules at 300 k will be : -
A300 m/secB610 m/secC920 m/secDzeroA particle moves on a path as shown. The particle takes 10 seconds in going from starting point to the final point. What is the average velocity vector of the particle ?
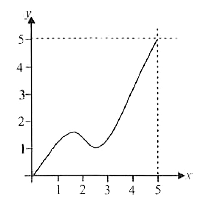 A0.5ˆi+ˆjB0.5ˆi+2.5ˆjC0.5ˆi+0.5ˆjDNone of these
A0.5ˆi+ˆjB0.5ˆi+2.5ˆjC0.5ˆi+0.5ˆjDNone of these
A particle is moving with a constant speed in a circular path. Find the ratio of average velocity to its instantaneous velocity when the particle rotates an angle θ=(π2) .
View SolutionA particle is moving with a constant speed v in a circle. What is the magnitude of average velocity after half rotation?
View SolutionTwo bodies are moving in opposite direction with speed V. What is the magnitude of their relative velocity ?
View SolutionThe magnitude of average velocity is equal to the average speed when a particle moves:-
View SolutionTwo particles are moving with velocities v1andv2 . Their relative velocity is the maximum, when the angle between their velocities is
View Solution