In figure, determine the character of the collision. The masses of the blocks, and the velocities before and after are given. The collision is
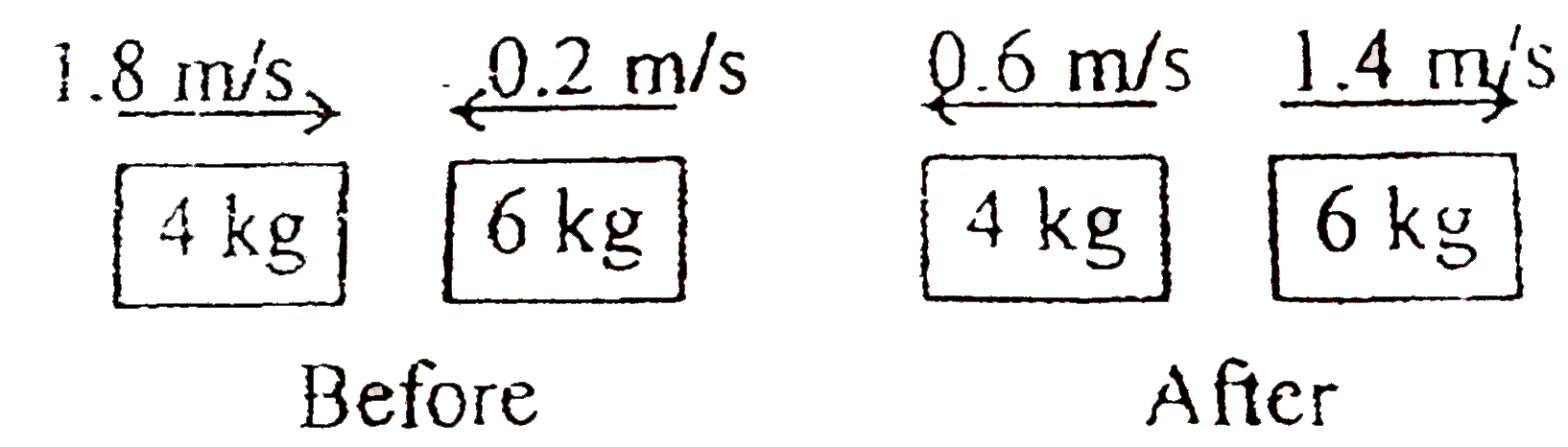
perfectly elastic
Partially inelastic
Completely inelastic
This collision is not possible
The correct Answer is:A
Ans.(1)
Linear momentum is conserverd and
e=Speed of separationSpeed of approach=1.4+0.61.8+0.2=1
So, collision of perfectly elastic.
Topper's Solved these Questions
- TEST PAPERBook:ALLENChapter:TEST PAPERExercise:PHYSICS
Explore 4 Videos
- TEST PAPERBook:ALLENChapter:TEST PAPERExercise:PHYSICS
Explore 4 Videos
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Example
Explore 1 Video
- TEST PAPER 1Book:ALLENChapter:TEST PAPER 1Exercise:PHYSICS
Explore 11 Videos
Similar Questions
An object of mass m is moving with velocity ữ towards a plane mirror kept on a stand as shown in the figure. The mass of the mirror and stand system is m. A head- on elastic collision takes place between the object and the mirror stand the velocity of image before and after the collision is
View SolutionA particle of mass m moving with velocity v0 collides with sphere of same mass at rest , as shown. If the surface of contact is smooth and the collision is elastic, find the velocities of particle and sphere after the collision.

View Solution
Knowledge Check
Three blocks of masses m , m and M are kept on a frictionless floor as shown in the figure .The leftmost block is given velocity v towards the right . All the collision between the blocks are perfectly inelastic . The loss in kinetic energy after all the collision is 5/6th of initial kinetic energy. The ratio of M/m will be
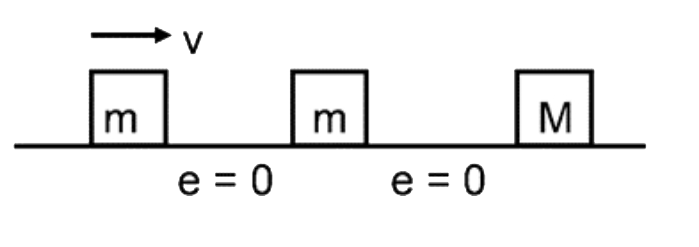 A14B18C2D4
A14B18C2D4A sphere of radius R and mass M collides elastically with a cubical block of mass M and side 2R. The entire system is on a smooth horizontal ground. Given that the sphere was rolling without slipping with an angular velocity ω at the time of collision. The velocities of the sphere and the block after the collision are
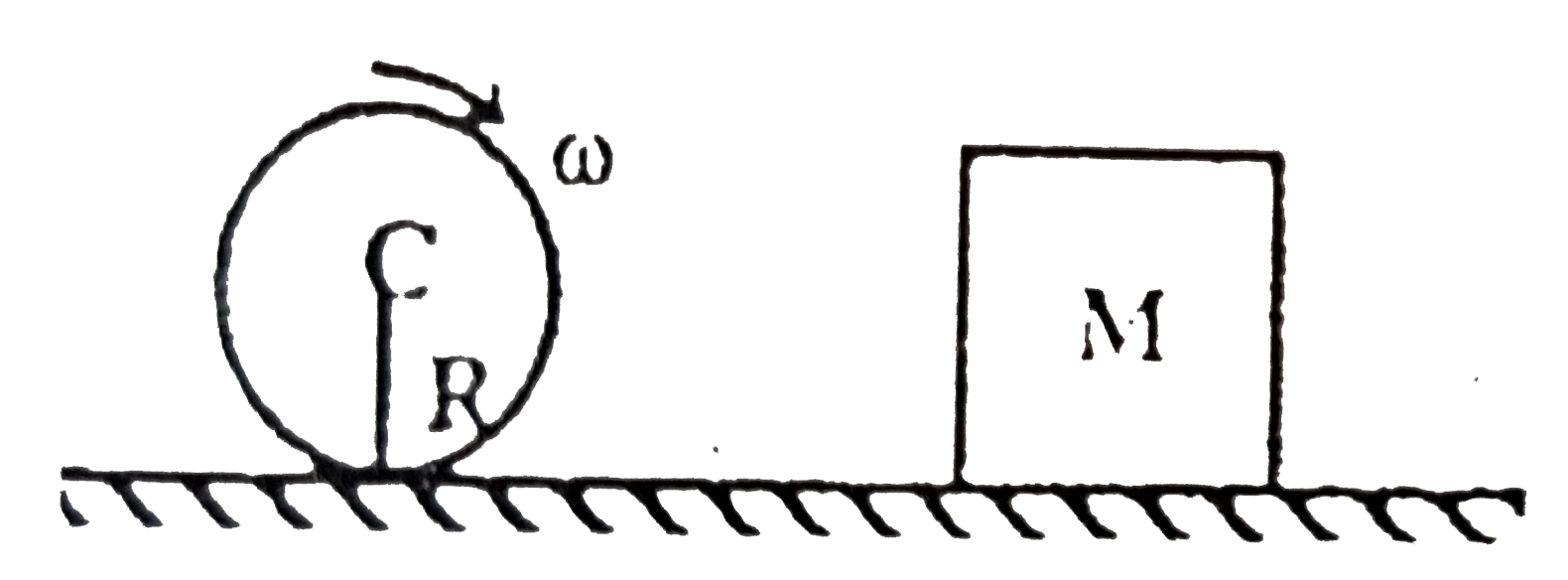 Aωsphere=0, vsphere=0, vblock=vBωsphere=ω, vsphere=0, vblock=vCωsphere=0, vsphere=0, vblock=0Dωsphere=ω2, vsphere=v2, vblock=v2
Aωsphere=0, vsphere=0, vblock=vBωsphere=ω, vsphere=0, vblock=vCωsphere=0, vsphere=0, vblock=0Dωsphere=ω2, vsphere=v2, vblock=v2A marble going at a speed of 2ms−1 hits another marble of equal mass at rest. If the collision is perfectly elastic, then the velocity of the first marble after collision is
A4ms−1B0ms−1C2ms−1D3ms−1
A uniform rod of length λ lies on a smooth horizontal table A particle moving on the table has a mass m and a speed v before the collision and it sticks to the rod after the collision. The rod has a mass M then find out.
The velocity of the centre of mass C and the angular velocity of the system about the centre of mass after the collision.
View SolutionOn a smooth carrom board. A coin located at (4,6) is moving in negative y−direction with speed 3m/s is being hit at that point by a striker moving along negative x− axis . The line joining centre of the coin and striker just before the collision is parallel to x− axis. After collision the coin goes into the hole located at origin. Mass of the striker and the coin is equal. Considering the collision to be elastic, find the velocity ( in vector form ) of the stricker before the collision and after the collision.
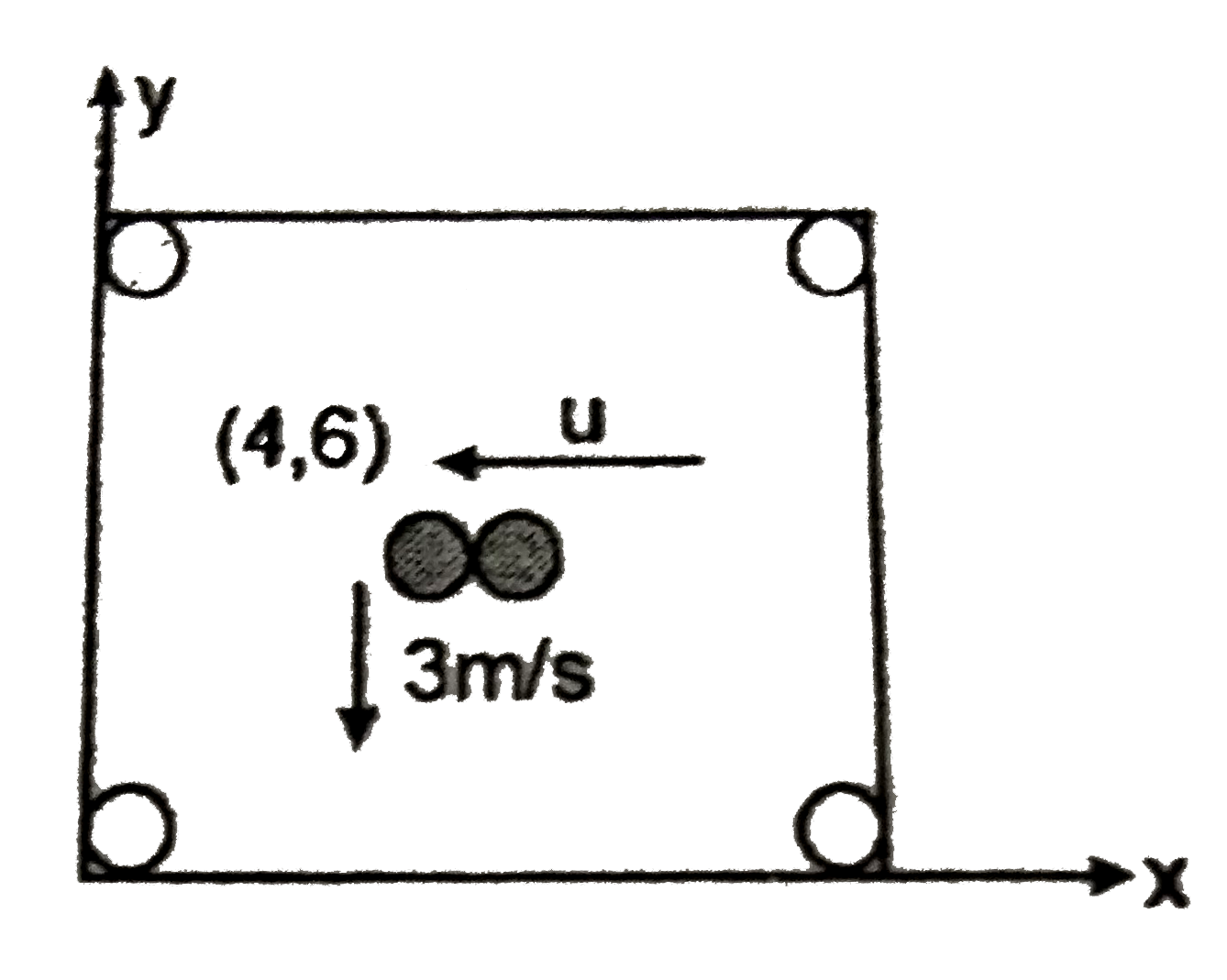
View SolutionA particle of mass m strikes another particle of same at rest. Find the angle between velocities of particles after the collision , if the collision is elastic.
View SolutionShow that in case of one dimensional elastic collision of two bodies, the relative velocity' of sepa¬ ration after the collision is equal to the relative velocity of approach before the collision
View SolutionAssertion:The principal of conservation of energy is valid for inelastic collision.
Reason: The principal of conservation of energy holds good in both elastic and inelastic collision. In case of inelastic collision kinetic energy before and after collision is not same.
View Solution

