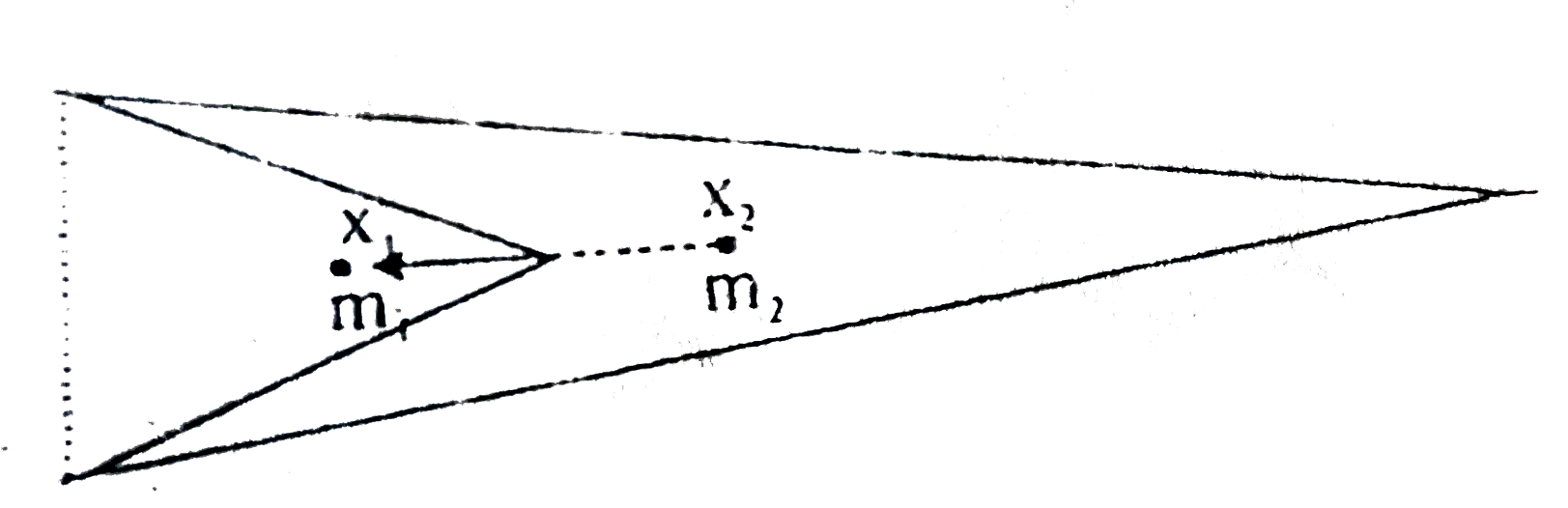
A uniformly thick plate in the shape of an arrow head has dimensions as shown. Find the distance of centre of mass from point O (in cm)

1
2
3
4
The correct Answer is:A
Ans.(1)
Note that the centre of mass of a uniform thick triangular sheet is at the centroid which divides a medium in a ratio 2:1. The required centre of mass must be on the line of symmetry passing through O and the vertex to the right . Consider the shape of arrowhead to be obtained by cuting the triangular part to the left (with base 6cm and height 3cm) from the uncut triangular sheet with base 6cm and height 9cm. The ratio of masses of these two is 3:1 the thickness being uniform.
XCM=m2x2−m1x1m2−m1=−1cm⇒ right of O
Topper's Solved these Questions
- TEST PAPERBook:ALLENChapter:TEST PAPERExercise:PHYSICS
Explore 4 Videos
- TEST PAPERBook:ALLENChapter:TEST PAPERExercise:PHYSICS
Explore 4 Videos
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Example
Explore 1 Video
- TEST PAPER 1Book:ALLENChapter:TEST PAPER 1Exercise:PHYSICS
Explore 11 Videos
Similar Questions
A uniformly thick plate in the shape of an arrow head has dimensions as shown in the figure. Find the distance (in cm ) of the centre of mass from point O.
'(##CEN_KSR_PHY_JEE_C08_E01_019_Q12##)'
View SolutionTwo uniform thin rods each of length L and mass m are joined as shown in the figure. Find the distance of centre of mass the system from point O

View Solution
Knowledge Check
The distance of centre of mass from O is
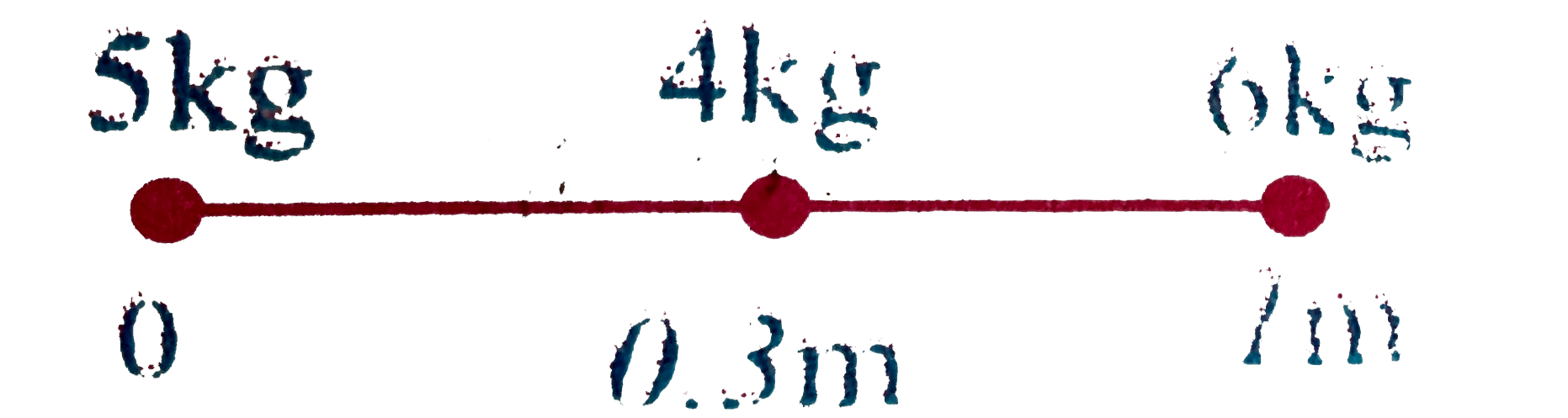 A0.21mB0.35mC0.42mD0.48m
A0.21mB0.35mC0.42mD0.48mA thin uniform rod of length L is bent at its mid point as shown in the figure. The distance of the centre of mass from the point O is
 AL2sin(θ2)BL2cos(θ2)CL4sin(θ2)DL4cos(θ2)
AL2sin(θ2)BL2cos(θ2)CL4sin(θ2)DL4cos(θ2)A uniform wire of length l is bent into the shape of 'V' as shown. The distance of its centre of mass from the vertex A is :-
 Al/2Bl√34Cl√38DNone of these
Al/2Bl√34Cl√38DNone of these
A square lamina of side a and a circular lamina of diameter a are placed touching each other as shown in figure. Find distance of their centre of mass from point O, the centre of sqaure.

View SolutionMass is non - uniformly distributed on the circumference of a ring of radius a and centre at origin . Let b be the distance of centre of mass of the ring from origin. Then ,
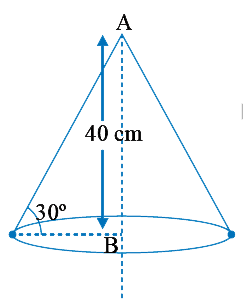
View SolutionA uniform solid cone of height 40 cm is shown in figure. The distance of centre of mass of the cone from point B (centre of the base) is :
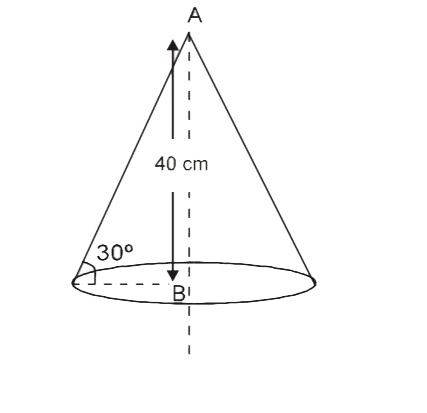
View SolutionA uniform solid cone of height 40 cm is shown in figure. The distance of centre of mass of the cone from point B (centre of the base) is :
View SolutionFrom a uniform square plate the shaped portions are removed as shown in figure. The coordinates of centre of mass of the remaining plate are x,y Axes and origon are shown in figure.
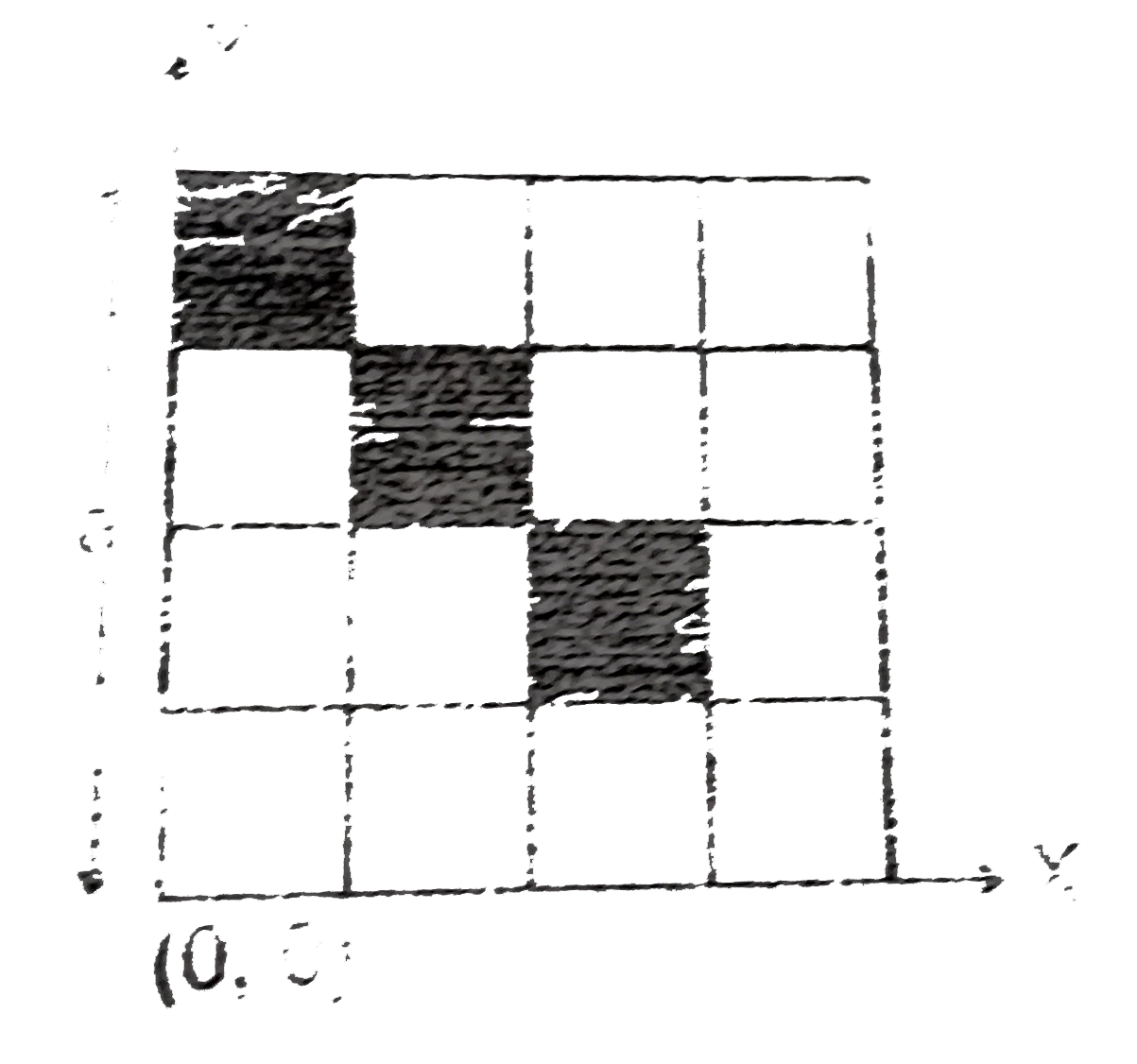
View Solution

