Two particles are projected at the same instant with speeds v1 and v2 making angles α and β with the horizontal as shown in the figure. Nelecting air resistance, the trajectory of the mass center the two particles

can be a vertical straight line
can be a horizontal straight line
is a straight line
is a parabola
The correct Answer is:A
Ans. (1)
If m1v1cosα≠m2v2, then centre of mass will move in a parabola.
If m1v1cosα=m2v2, then centre of mass will move in straight line.
Topper's Solved these Questions
- TEST PAPERBook:ALLENChapter:TEST PAPERExercise:PHYSICS
Explore 4 Videos
- TEST PAPERBook:ALLENChapter:TEST PAPERExercise:PHYSICS
Explore 4 Videos
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Example
Explore 1 Video
- TEST PAPER 1Book:ALLENChapter:TEST PAPER 1Exercise:PHYSICS
Explore 11 Videos
Similar Questions
Two particles are simultaneously projected in the same vertical plane from the same point with velocities u and v at angles αandβ with horizontal. Find the time that elapses when their velocities are parallel.
View SolutionTwo particles are projected at the same instant from the same point of inclinations α and β to the horizontal.if they simultaneously hit the top and the bottom of a vertical pole subtending an angle γ at the point of projection, show that tan−αtanβ=tanγ.
View Solution
Knowledge Check
Two particles of equal mass 'm' are projected from the ground with speed v1 and v2 at angles θ1 and θ2 at the same times as shown in figure. The centre of mass of the two particles.
 Awill move in a vertical line if v1tanθ=v2tanθ2Bwill move in a vertical line if v1sinθ=v2sinθ2Cwill move In a vertical line if v1cotθ1=v2cotθ2Dwill move in a vertical line if v1cosθ1=v2cosθ2
Awill move in a vertical line if v1tanθ=v2tanθ2Bwill move in a vertical line if v1sinθ=v2sinθ2Cwill move In a vertical line if v1cotθ1=v2cotθ2Dwill move in a vertical line if v1cosθ1=v2cosθ2Two particles A and B are projected from the same point with the same velocity of projection but at different angles αand β of projection, such that the maximum height of A is two-third of the horizontal range of B. then which of the following relations are true?
Arange of A= maximum height of BB3(1−cos2α)=8sin2βCmaximum value of β is sin−1(3/4)Dmaximum horizontal range of A =u2/g and this occurs when β=12sin−1(38)Trajectory of two particles projected from origin with speeds v1 and v2 at angles θ1 and θ2 with positive x- axis respectively are as shown in the figure. Given that (g=−10m/s2(ˆj)). Choose the correct option related to diagram.
 Av1−v2=2v1Bθ2−θ1=2θ1C3(v1−v2)=v1D3(θ2−θ1)=θ1
Av1−v2=2v1Bθ2−θ1=2θ1C3(v1−v2)=v1D3(θ2−θ1)=θ1
Two projectiles are thrown simultaneously in the same plane from the same point. If their velocities are v1 and v2 at angles θ1 and θ2 respectively from the horizontal, then ansewer the following questions
The trajectory of particle 1 with respect to particle 2 wil be
View SolutionTwo particles are projected with same speed but at angles of projection (45∘−θ) and (45∘+θ). Then their horizontal ranges are in the ratio of
View SolutionTwo particles are projected in air with speed v0 at angles θ1 and θ2 (both acute) to the horizontal,respectively.If the height reached by the first particle greater than that of the second,then thick the right choices
View SolutionTwo particles of equal mass in are projected from the ground with speeds v1 and v2 at angles θ1, and θ2 as shown in the figure. Given θ2>θ1 and v1cosθ1=v2cosθ2Which statement/s is/are correct?
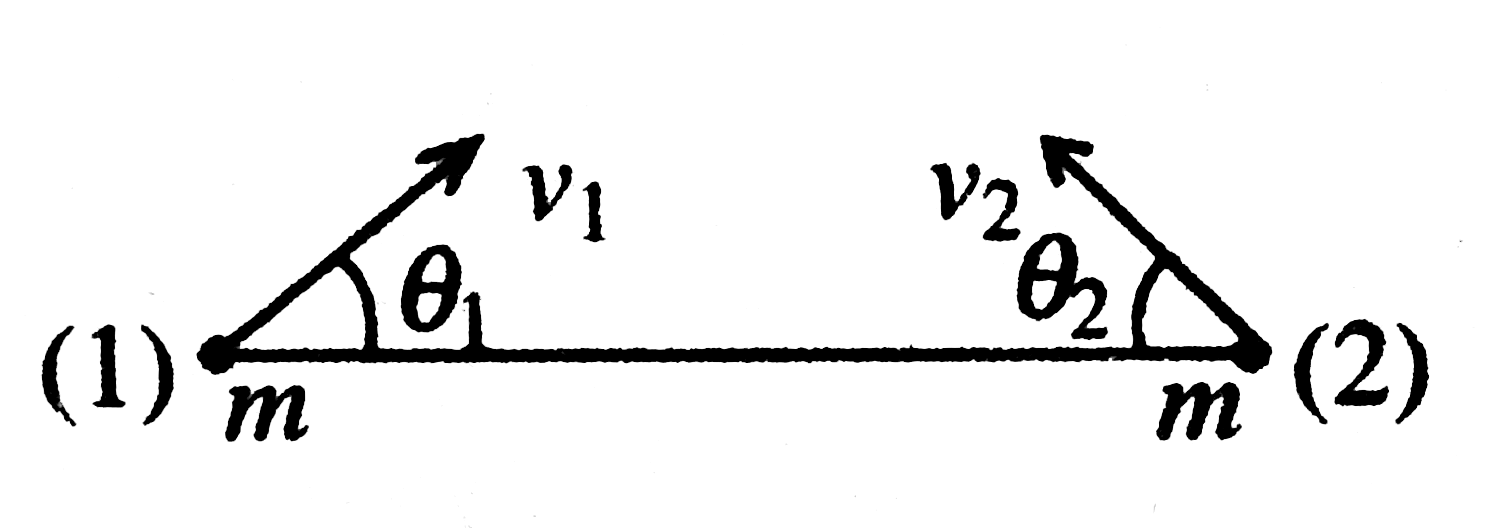
View SolutionA projectile is projected with a velocityv0 at an angle θ with the horizontal as shown in figure. The angular momentum of particle about the origin:

View Solution

