A perfectly absobing, black, solid sphere with constant density and radius R, hovers stationary above the sun. This is because the gravitational attraction of the sun is balanced by the pressure due to the sun's light. Assume the sun is far enough away that it closely approximates a point source of light. The distance from the centre of the sun at which the sphere hovers is :
proportional to R
proportional to 1/R
proportional to 1/R2
independent of R
The correct Answer is:D
(IC)×πR2=GMs(p(4/3)πR3)x2
(IC)πR2=GMsp43πR3
(Et4πx2)×1C×πR2=GMs(p(4/3)πR3)x2
x is independent of R

Topper's Solved these Questions
Similar Questions
A perfectly absorbing solid sphere with a known fixed density, hovers stationary above the sun. This is because the gravitational attraction of the sun is balanced by the pressure due to the sun’s light. Assume the sun is far enough away so that it closely approximates a point source of light. Find the radius of the sphere and prove that it is independent of the distance of the sphere from the Sun.
View SolutionA uniform solid of valume mass density ρ and radius R is shown in figure.
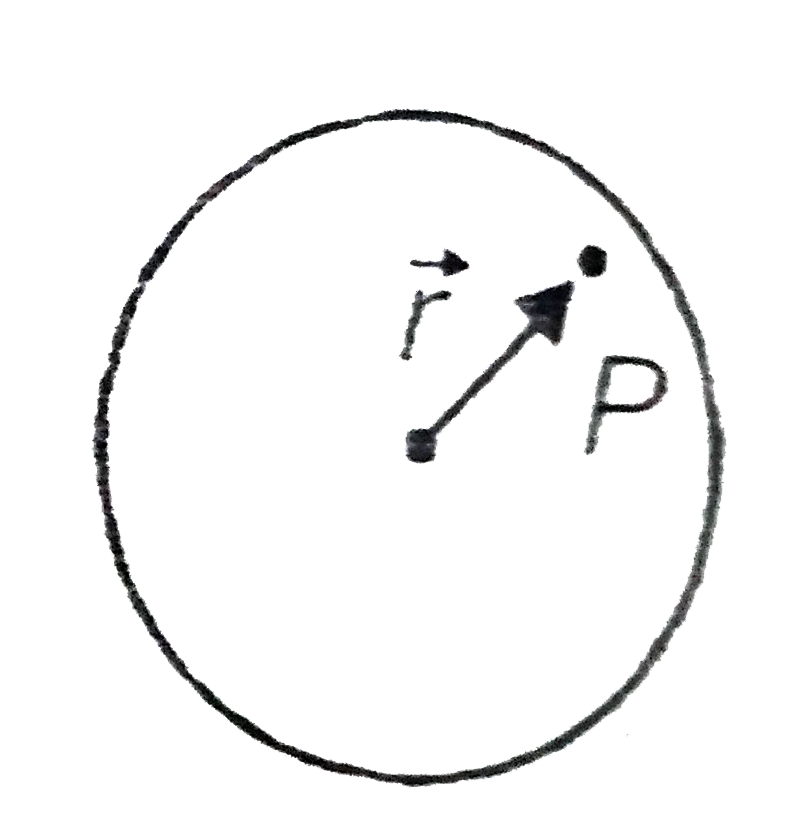
(a) Find the gravitational field at a point P inside the sphere at a distance r from the centre of the sphere. Represent the gravitational field vector →l in terms of radius vector →r of point P.
(b) Now a spherical cavity is made inside the solid sphere in such a way that the point P comes inside the cavity. The centre is at a distance a from the centre of solid sphere and point P is a distance of b from the centre of the cavity. Find the gravitational field →E at point P in vector formulationand interpret the result.
View Solution
Knowledge Check
A point mass m is released from rest at a distance of 3R from the centre of a thin-walled hollow sphere of radius R and mass M as shown. The hollow sphere is fixed in position and the only force on the point mass is the gravitational attraction of the hollow sphere. There is a very small hole in the hollow sphere through which the point mass falls as shown. The velocity of a point mass when it passes through point P at a distance R/2 from the centre of the sphere is
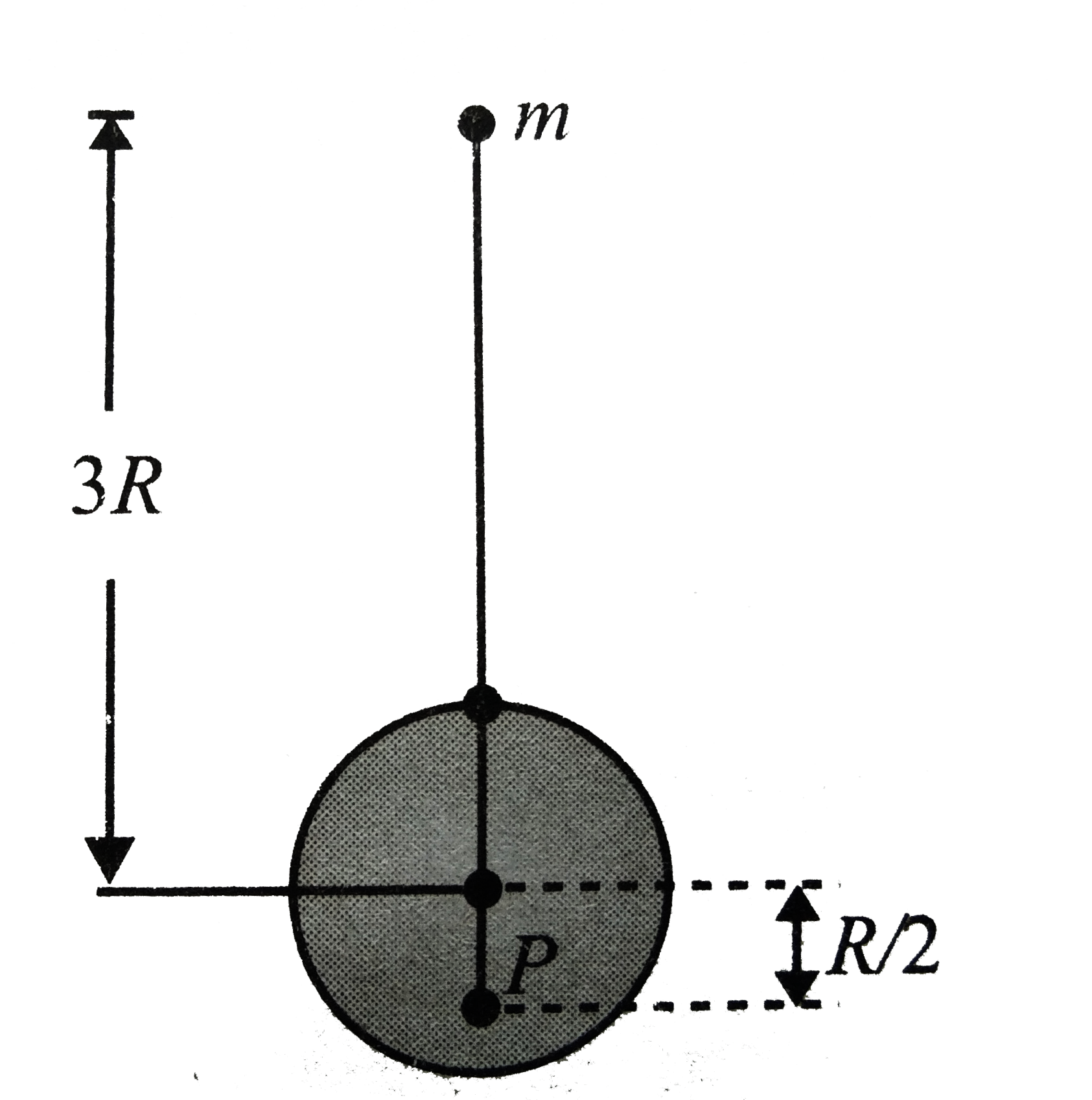 A√2GM3RB√5GM3RC√25GM24RDnone of these
A√2GM3RB√5GM3RC√25GM24RDnone of theseConsider the sun as a black body of radius 7×108 m and the earth receiving its surface radiations from the sun at a rate of approximately 1500W/m2 . If the distance of the centre of the sum from the earth's surface is 15×1010 m, then the surface temperature of the sun is
A4990.5 KB5706.8 KC5903.7KD6063.4 KThe motion of a planet around sun in an elliptical orbit is shown in the following figure. Sun is situated at one focus. The shaded areas are equal. If the planet takes time t1 and l2 in moving from A to B and from C to D respectively, then
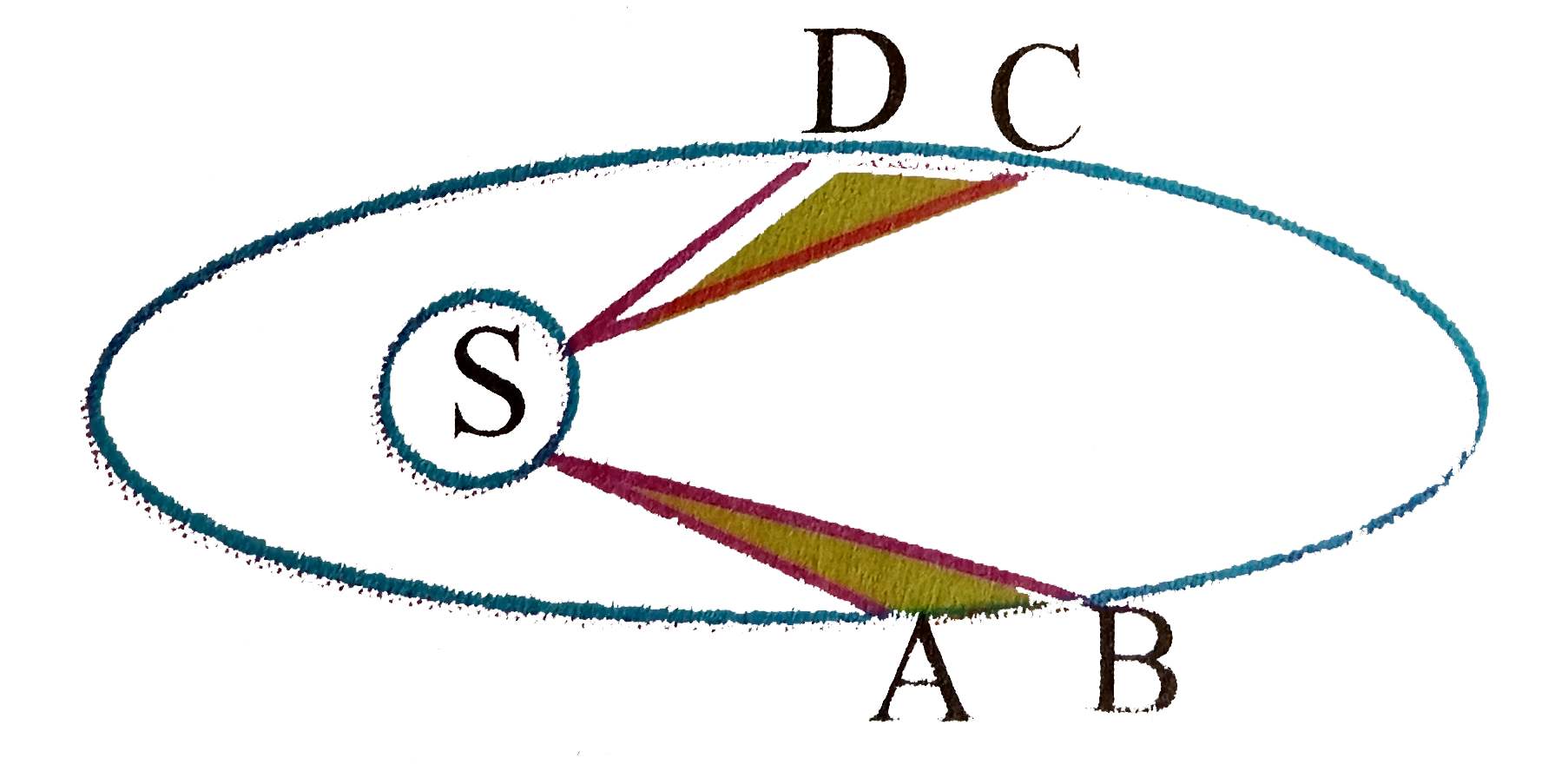 A3GMmaB5GMmaCGMmaDnone of the above
A3GMmaB5GMmaCGMmaDnone of the above
Assuming a particle to have the form of a ball and to absorb all incient light, find the radius of a particle for which its gravitational attraction to the sun is counterbalanced by the forces that light exerts on it. The power of light raiated by the sun equals P=4.1026W, and the density of the particle is ρ=1.0g/cm3.
View SolutionA planet of radius r0 is at a distance r from the sun (r>>r0). The sun has radius R. Temperature of the planet is T0, and that of the surface of the sun is Ts. Calculate the temperature of another planet whose radius is 2r0 and which is at a distance 2r from the sun. Assume that the sun and the planets are black bodies.
View SolutionA projectile is to be launched from the surface of the earth so as to escape the solar system. Consider the gravitational force on the projectile due to the earth and the sun nly. The projectile is projected perpendicular to the radius vector of the earth relative to the centre of the sun in the direction of motion of the earth. Find the minimum speed of projection relative to the earth so that the projectile escapes out of the solar system. Neglect rotation of the earth. mass if the sum Ms2×1030kg, Mass of the earth Me=6.4×1024kg Radius if the earthRe=6.4×106m, Earth- Sun distence r=1.5×1011m
View SolutionThe motion of a planet around sun in an elliptical orbit is shown in the following figure. Sun is situated at one focus. The shaded areas are equal. If the planet takes time t1 and l2 in moving from A to B and from C to D respectively, then
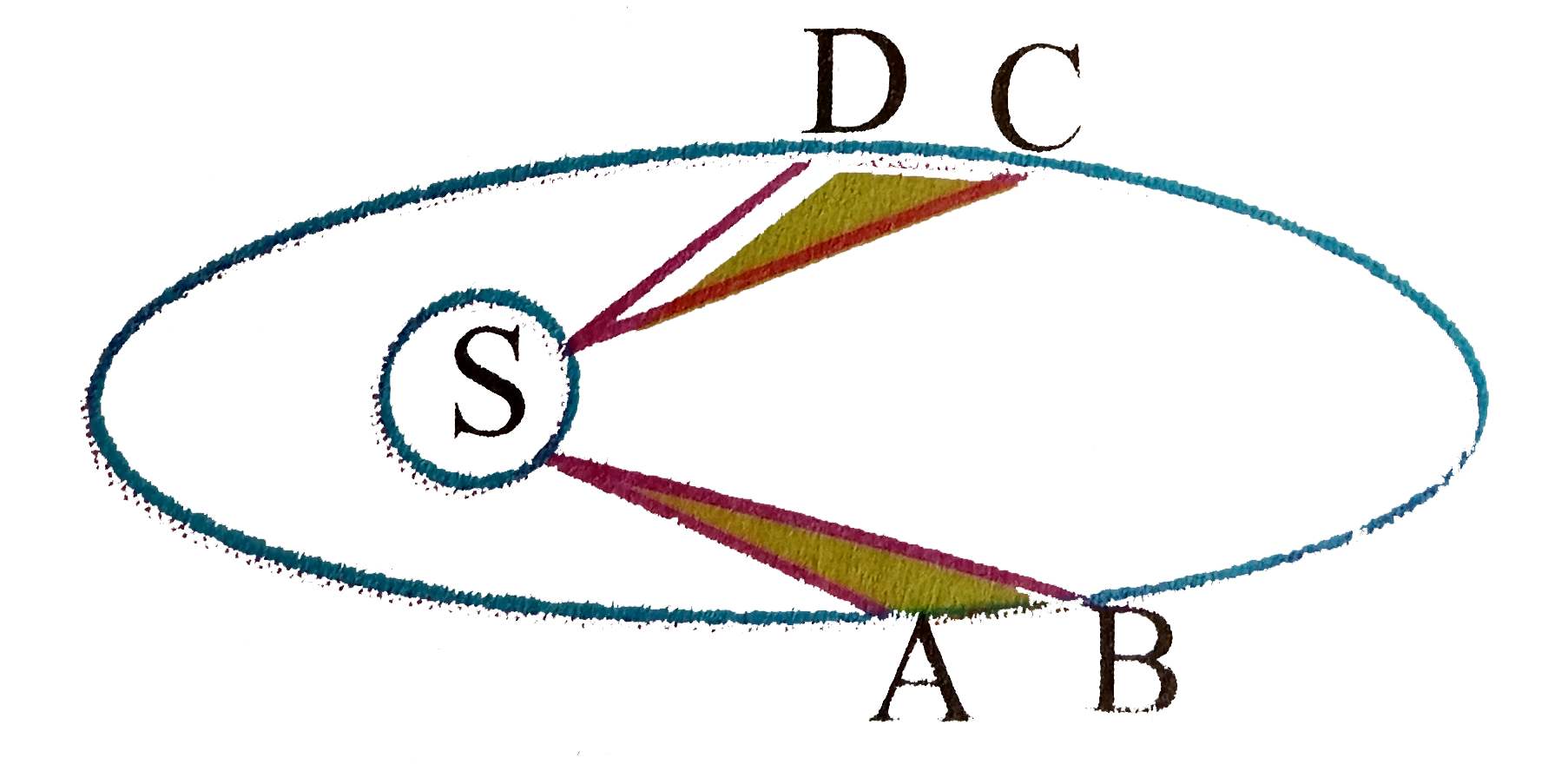
View SolutionAssuming the sun to have a spherical outer surface of radius r, radiating like a black body at temperature t∘c, the power received by a unit surface, (normal to the incident rays) at a distance R from the centre of the sun is
where σ is the Stefan's constant.
View Solution