A wire ring of radius R is fixed in a horizontal plane. The wire of the ring has a resistance of λΩm–1. There is a uniform vertical magnetic field B in entire space. A perfectly conducting rod (l) is kept along the diameter of the ring. The rod is made to move with a constant acceleration a in a direction perpendicular to its own length. Find the current through the rod at the instant it has travelled through a distance x=R2.
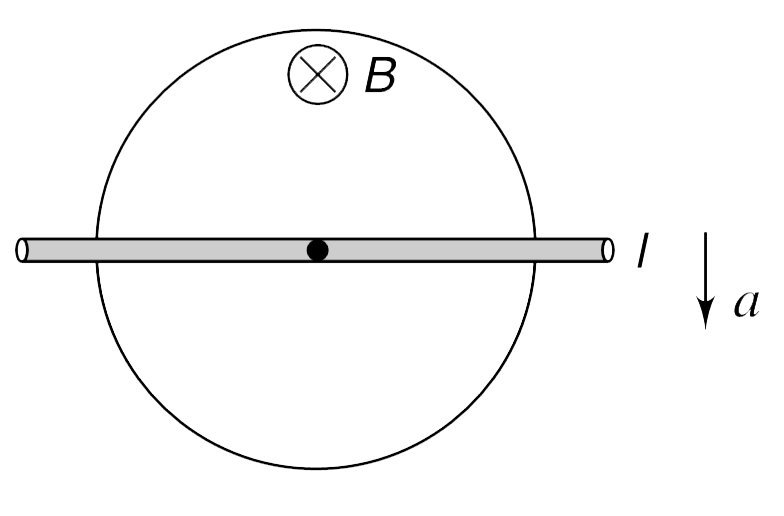
The correct Answer is:18B5π√3aRλ
Step by step video, text & image solution for A wire ring of radius R is fixed in a horizontal plane. The wire of the ring has a resistance of lambda Omega m^(–1). There is a uniform vertical magnetic field B in entire space. A perfectly conducting rod (l) is kept along the diameter of the ring. The rod is made to move with a constant acceleration a in a direction perpendicular to its own length. Find the current through the rod at the instant it has travelled through a distance x = (R)/(2). by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - ARIHANTCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 2
39 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - ARIHANTCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 3
12 Videos
- CURRENT ELECTRICITYBOOK - ARIHANTCHAPTER - CURRENT ELECTRICITYEXERCISE - Current Electricity
105 Videos
- ELECTROSTATICSBOOK - ARIHANTCHAPTER - ELECTROSTATICSEXERCISE - Level 3
59 Videos
Similar Questions
A conducting ring of radius r and resistance R is placed in region of uniform time varying magnetic field B which is perpendicular to the plane of the ring. It the magnetic field is changing at a rate α, then the current induced in the ring is
View SolutionUniform magnetic field B, exists in the vertical downward direction. A rod whose length is kept horizontal and is moved with velocity v perpendicular to its length. Motional emf developed across the length of the rod is
View Solution
Knowledge Check
A horizontal ring of radius r spins about its axis with an angular velocity ω in a uniform vertical magnetic field of magnitude B. The emf induced in the ring is
AzeroBπr2ωBC12Br2ωDBr2ωA ring of radius R is rolling on a horizontal plane with constant velocity v. There is a constant and uniform magnetic field B which is perpendicular to the plane of the ring. Emf across the lowest point A and right-most point C as shown in the figure will
 AIncrease with timeBdecrease with timeCremains constant and equal to √2BvRDremains constant and equal to BvR
AIncrease with timeBdecrease with timeCremains constant and equal to √2BvRDremains constant and equal to BvRA wire is bent in the form of a V shape and placed in a horizontal plane. There exists a uniform magnetic field B perpendicular to the plane of the wire. A uniform conducting rod starts sliding over the V shaped wire with a constant speed v as shown in the figure. If the wire no resistance, the current in rod wil
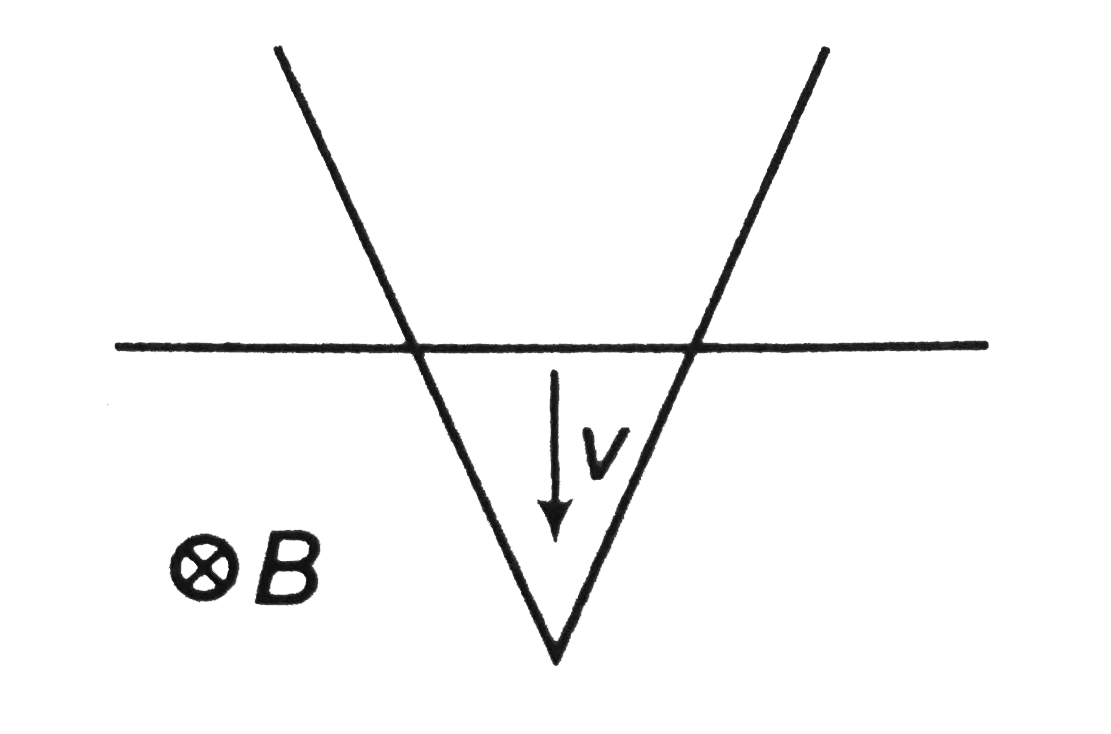 Aincrease with timeBdecrease with timeCremain constantDalways be zero
Aincrease with timeBdecrease with timeCremain constantDalways be zero
A ring rotates with angular velocity ω about an axis in the plane of the ring which passes through the center of the ring. A constant magnetic field B exists perpendicualr to the plane of the ring . Find the emf induced in the ring as a function of time.

View SolutionA conducting ring of radius 2R rolls on a smooth horizontal conducting surface as shown in figure-5.295. A uniform horizontal magnetic field B is perpendicular to the plane of the ring. The potential of A with respect to O is:

View SolutionIn figure, there is conducting ring having resistance R placed in the plane of paper in a uniform magnetic field B0. If the rings is rotating in the plane of paper about an axis passing through point O and perpendicular to the plane of paper with constant angular speed ω in clockwise direction, then
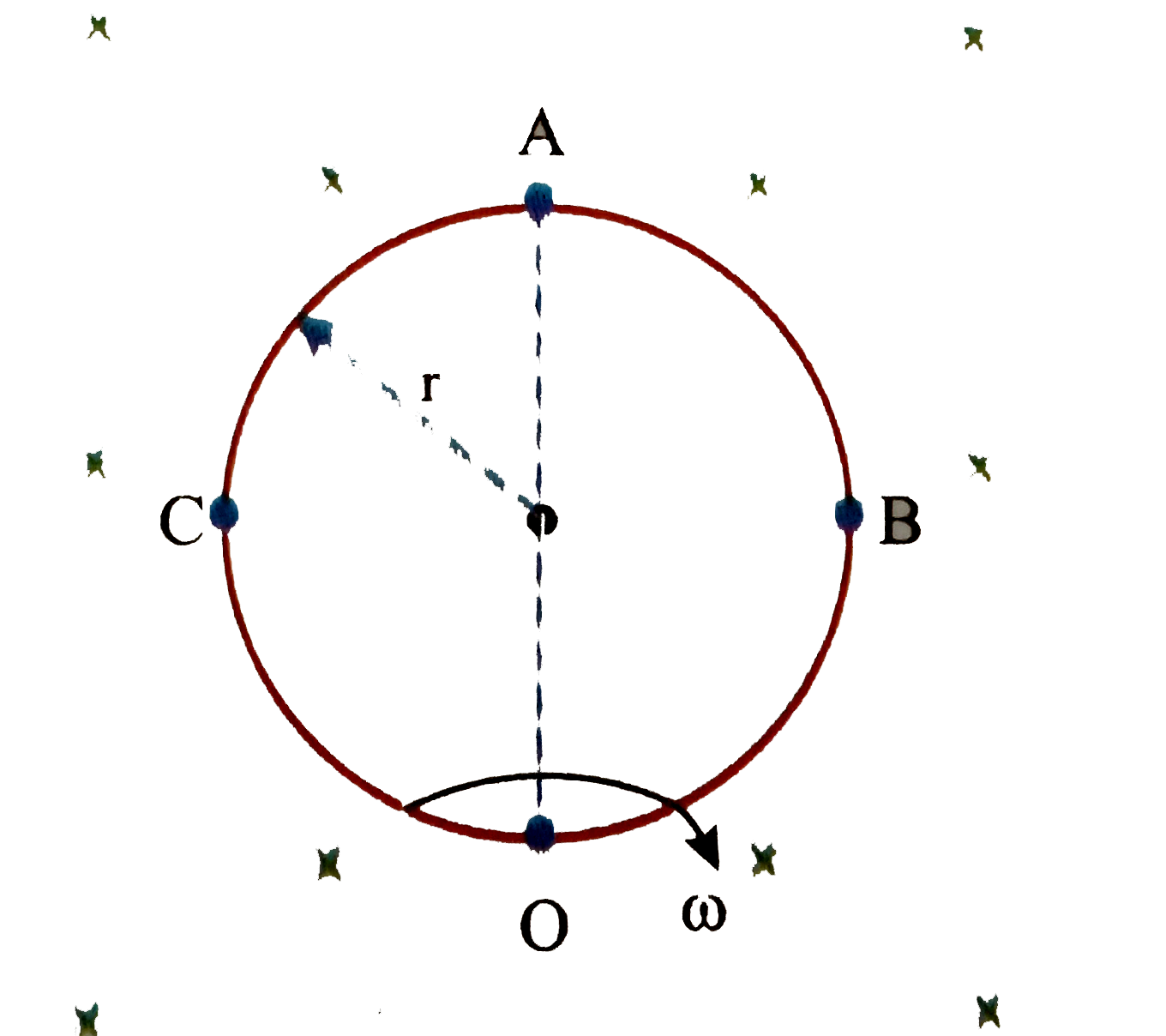
View SolutionA conducting ring of radius r is placed in a varying magnetic field perpendicular to the plane of the ring. If the rate at which the magnetic field varies is x, the electric field intensity at any point of the ring is
View SolutionAB is a resistanceless conducting rod which forms a diameter of a conducting ring of radius r rotating in a uniform magnetic field B as shown in figure. The resistance R1 and R2 do not rotate. Then the current through the resistor R1 is
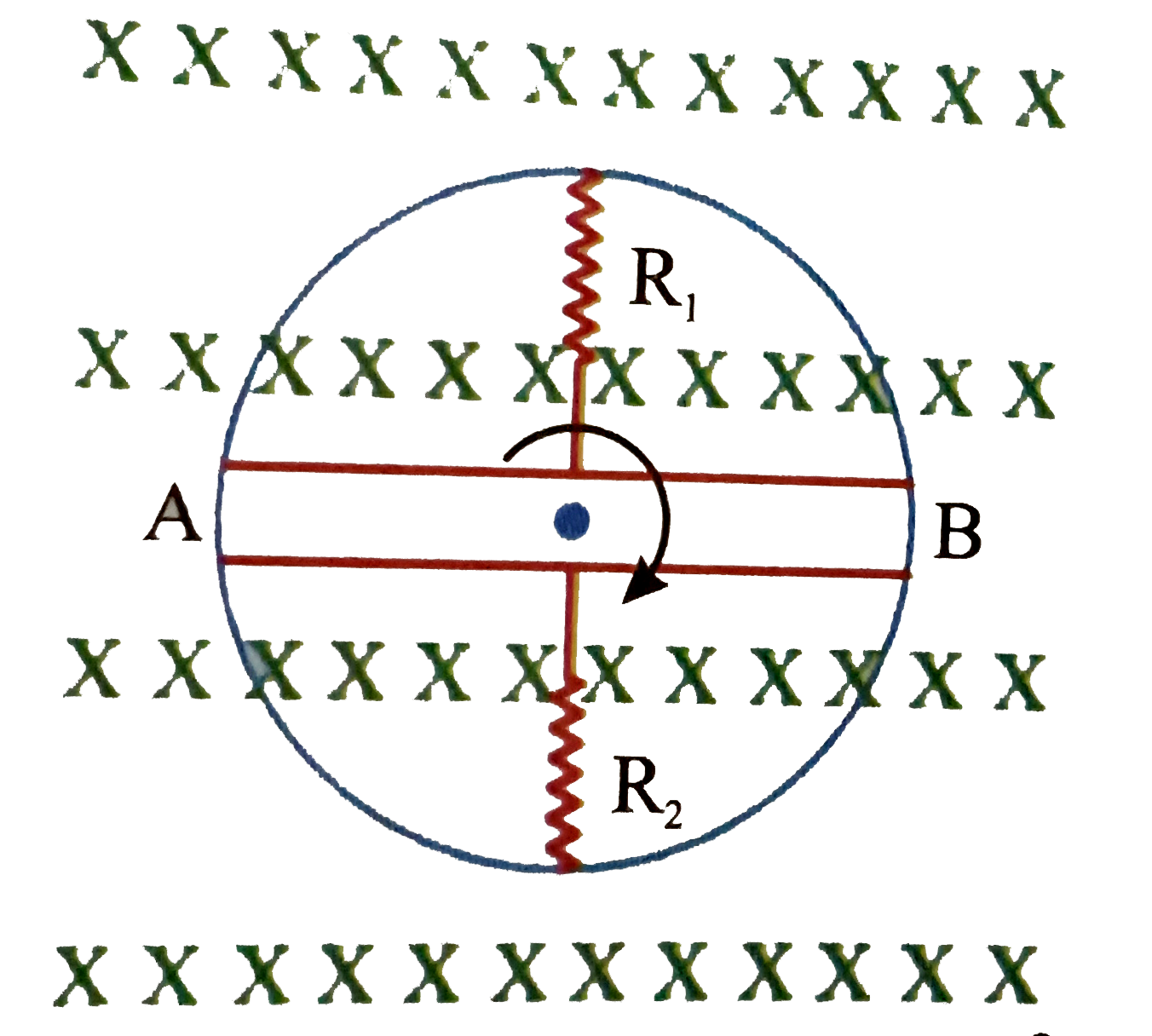
View Solution
