Consider two spheres of the same radius R having uniformly distributed volume charge density of same magnitude but opposite sign (+ρ and −ρ) the spheres overlap such that the vector joining the centre of the negative sphere to that of the positive sphere is →d. (d<<R). Find magnitude of electric field at a point outside the spheres at a distance r in a direction making an angle θ with →d. Distance r is measure with respect to the mid point of the line joining the centers of the two spheres.
The correct Answer is:ρR3d3ε0r3√3cos2θ+1
Step by step video, text & image solution for Consider two spheres of the same radius R having uniformly distributed volume charge density of same magnitude but opposite sign (+rho and -rho) the spheres overlap such that the vector joining the centre of the negative sphere to that of the positive sphere is vecd. (d lt lt R). Find magnitude of electric field at a point outside the spheres at a distance r in a direction making an angle theta with vecd. Distance r is measure with respect to the mid point of the line joining the centers of the two spheres. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A solid sphere of radius R has total charge Q. The charge is distributed in spherically symmetric manner in the sphere. The charge density is zero at the centre and increases linearly with distance from the centre. (a) Find the charge density at distance r from the centre of the sphere. (b) Find the magnitude of electric field at a point ‘P’ inside the sphere at distance r1 from the centre.
View SolutionA solid of radius 'R' is uniformly charged with charge density ρ in its volume. A spherical cavity of radius R2 is made in the sphere as shown in the figure. Find the electric potential at the centre of the sphere.

View Solution
Knowledge Check
A non-conducting solid sphere of radius R is uniformly charged. The magnitude of the electric filed due to the sphere at a distance r from its centre
A(a) increases as r increases, for r<R.B(b) decreases as r increases, for 0<r<∞.C(c) decreases as r increases, for R<r<∞.D(d) is discontinuous at r=R.Potential difference beween centre and surface of the sphere of radius R and uniorm volume charge density ρ within it will be
AρR26ε0BρR24ε0CρR23ε0DρR22ε0A non-conducting solid sphere of radius R is uniformly charged. The magnitude of the electric filed due to the sphere at a distance r from its centre
AIncreases as r increases inside the sphereBDecreases as r increases inside as well as outsideCIncreases as increases outside the sphereDIs discontinuousat r=R
A solid non conducting sphere of radius R has a non-uniform charge distribution of volume charge density, ρ=ρ0rR, where ρ0 is a constant and r is the distance from the centre of the sphere. Show that : (i) the total charge on the sphere is Q=πρ0R3 (ii) the electric field inside the sphere has a magnitude given by, E=KQr2R4
View SolutionA hallow metal sphere of radius R is uniformly charged. The electric field due to the sphere at a distance r from the centre:
View SolutionThere is a solid sphere of radius R having uniformly distributed charge throughout it. What is the relation between electric field E and distance r from the centre (r lt R) ?
View SolutionA positively charge sphere of radius r0 carries a volume charge density ρ. A spherical cavity of radius r0/2 is then scooped out and left empty. C1 is the center of the sphere and C2 that of the cavity. What is the direction and magnitude of the electric field at point B?

View SolutionFigure shown four solid spheres, each with charge Q uniformly distributed through its volume. The figure also shows a point P for each sphere. All at the same distance from the centre of the sphere. Rank the spheres according to the magnitude of the electric field they produce at point P.
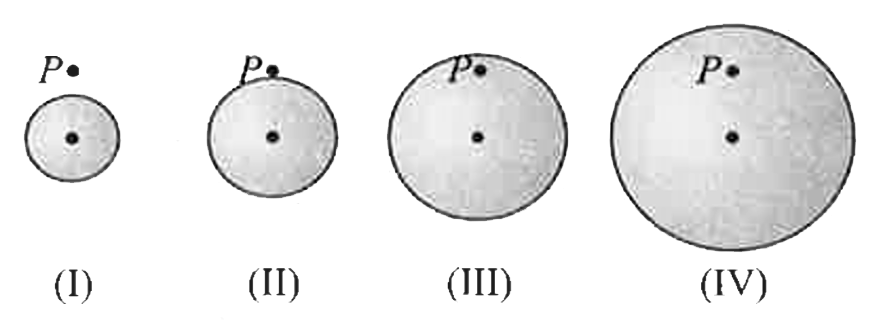
View Solution