An infinite line cahrge is perpendicular to the plane of the figure having linear charge density λ, A partcle having charge Q and mass m is projected in the field of the line cahrge fromo point P. the point P is at a distance R from the line cahrge and velocity given tot he particle is perpendicular tot he radial line at P (see figure)
(i). Find the speed of the particle when its distance from the line cahrge grows the ηR(η>1)
(ii). Find the velocity component of the particle along the radial line (joining the line charge to the particle) at the instant its distance becomes ηR.

The correct Answer is:(a) V=√V20+λQπε0mlnη
(b). Vr=√V20(1−1η2)+λQπε0mlnη
Step by step video, text & image solution for An infinite line cahrge is perpendicular to the plane of the figure having linear charge density lamda, A partcle having charge Q and mass m is projected in the field of the line cahrge fromo point P. the point P is at a distance R from the line cahrge and velocity given tot he particle is perpendicular tot he radial line at P (see figure) (i). Find the speed of the particle when its distance from the line cahrge grows the etaR(eta gt 1) (ii). Find the velocity component of the particle along the radial line (joining the line charge to the particle) at the instant its distance becomes etaR. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
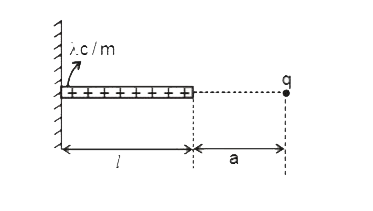
Find the total force on charge q due to a charge rod having linear charge density λCm placed as shown in figure.
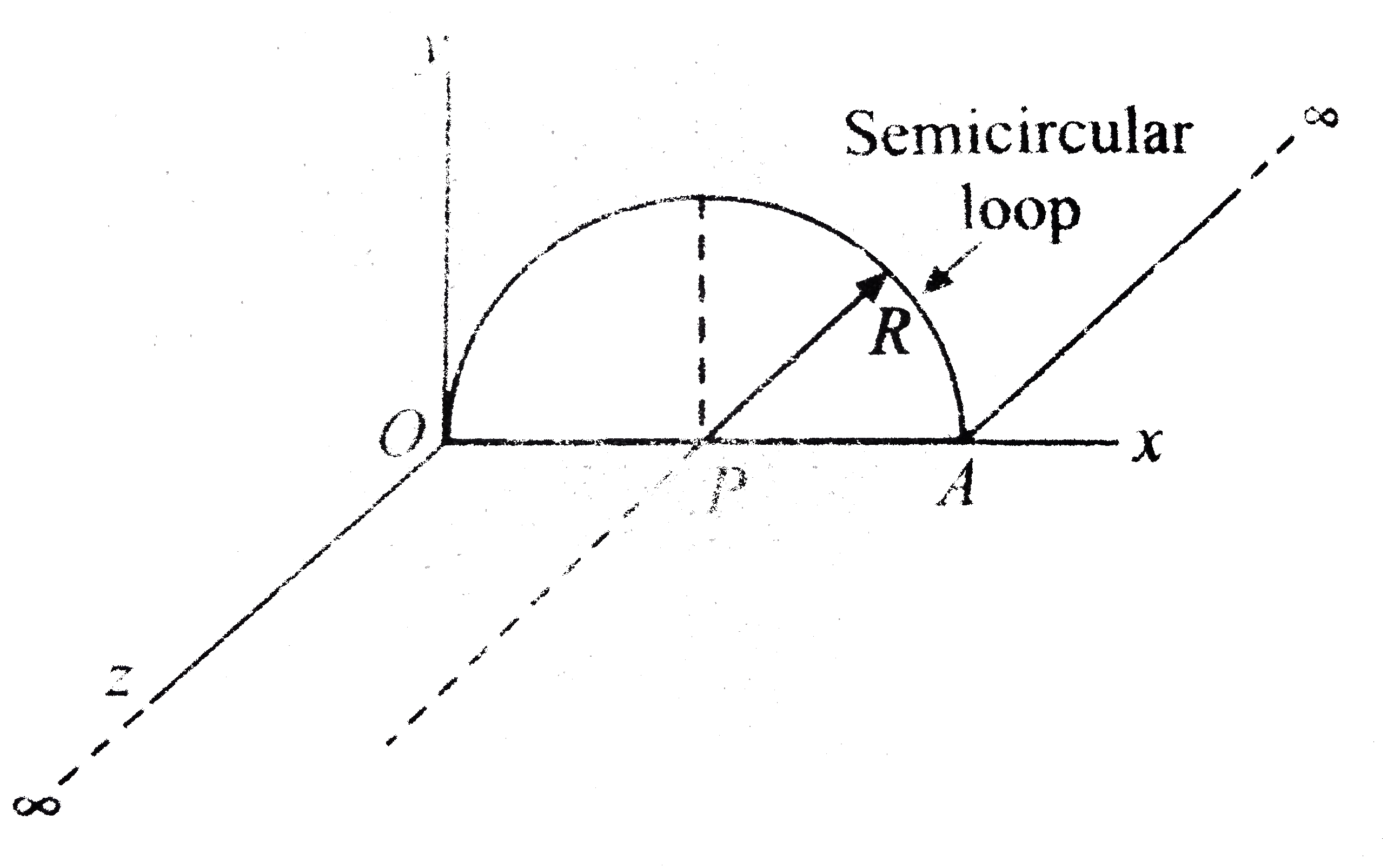
View SolutionAn infinte wire having linear charge density λ is arranged as shown in fig. A charge particle of mass m and charge q is released charged q is released from point P. Find the initial acceleration of the particle just after the particle is released.
View Solution
Knowledge Check
An infinite line charge produces a field of 4.5×104N/C at a distance 2 m from it. The linear charge density is
A5μC/mB6μC/mC4μC/mD7μC/mMass M is distributed uniformly along a line of length 2L. A particle of mass m is at a point that is at a distance a above the centre of the line on the its perpendicular bisector (Point P in figure). The gravitational force that the line exert on the particle is
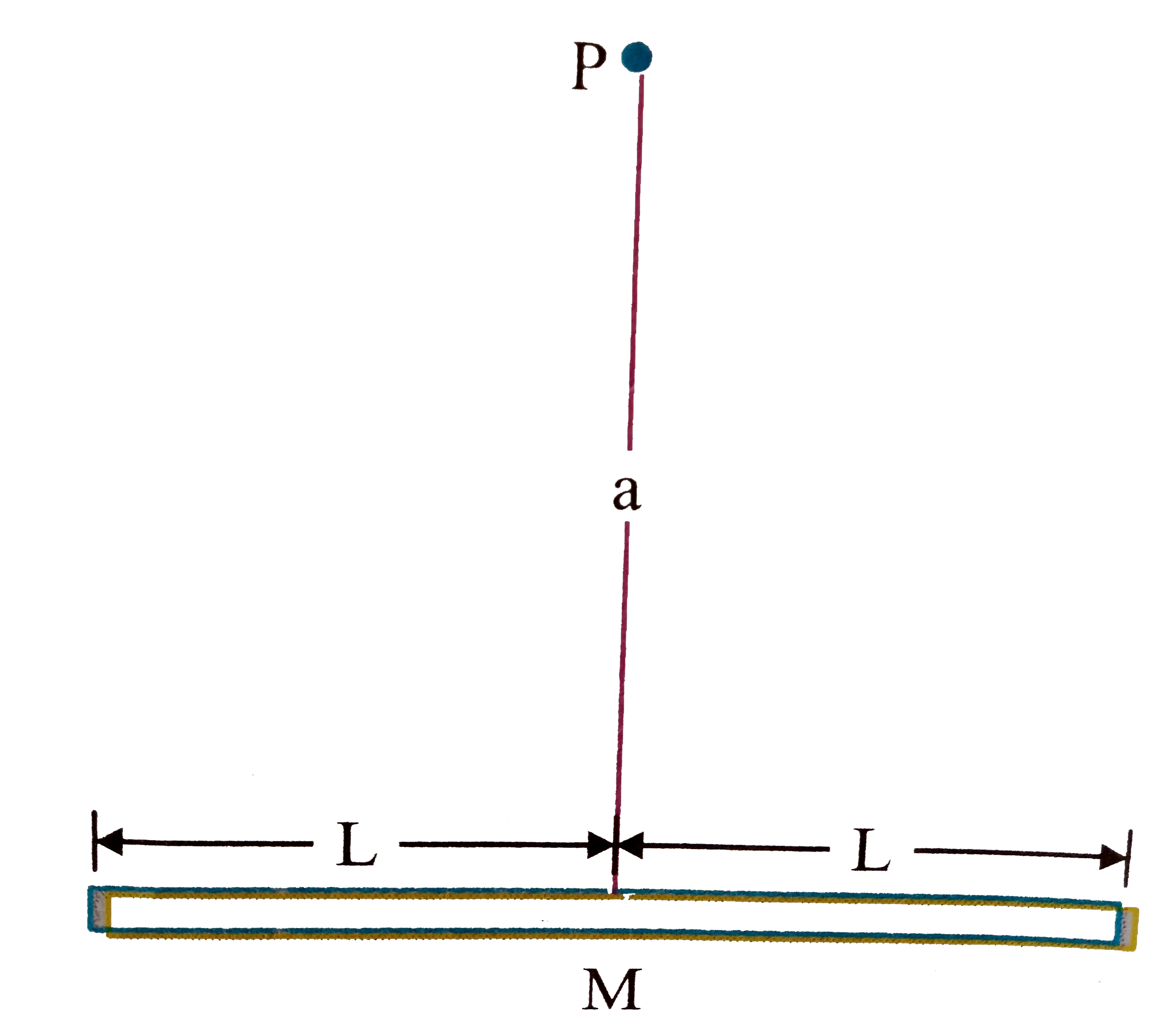 AGMm√L2+a2BGMma(L2+a2)CGMma√L2+a2DGMma(L2+a2)2
AGMm√L2+a2BGMma(L2+a2)CGMma√L2+a2DGMma(L2+a2)2The minimum distance of origin from the plane passing through the point with position vector P and perpendicular to the lineL2 is:
A√14B7√14C11√14DNone of these
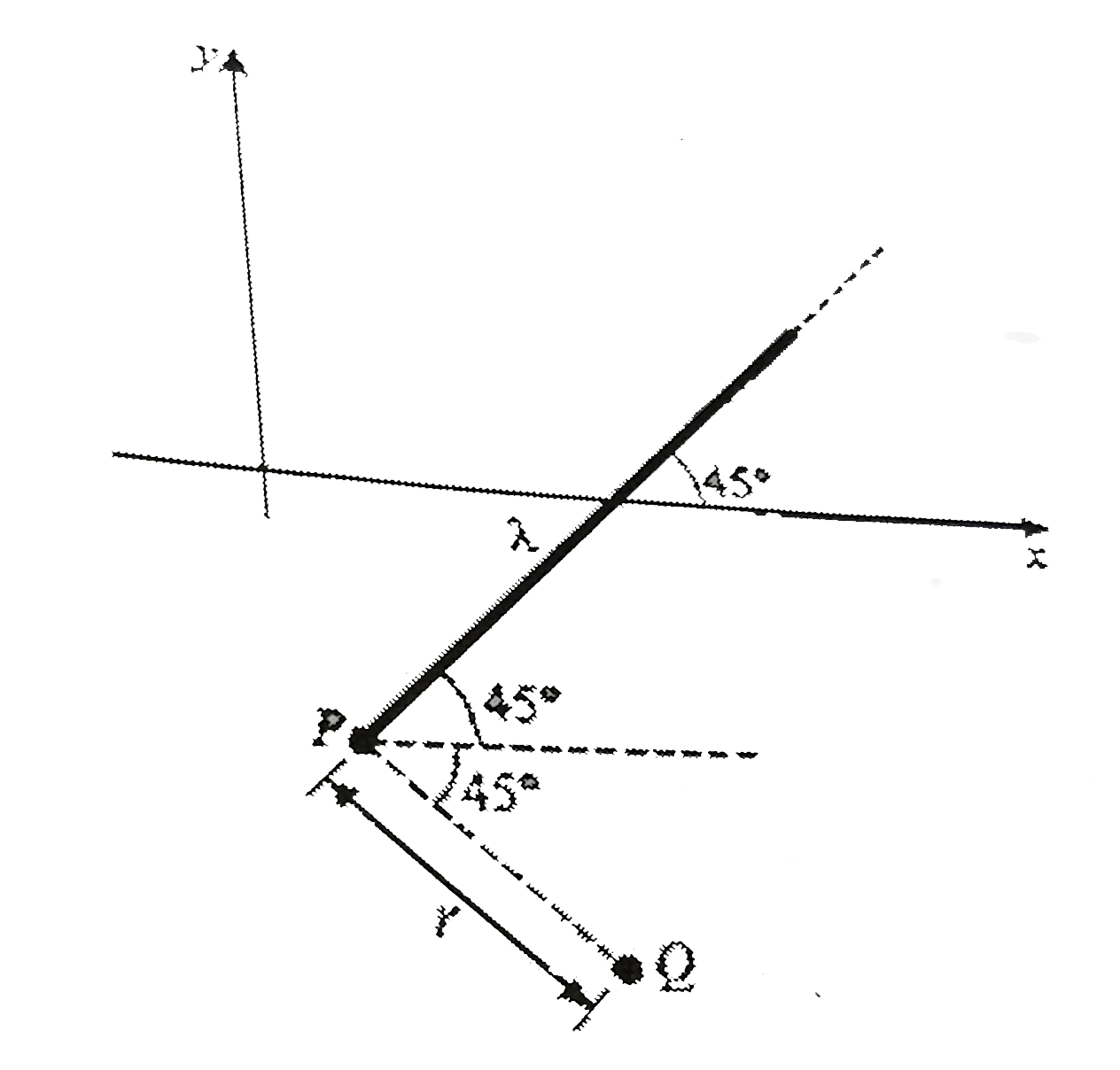
A very long charged wire (lying in the xy plane ) which is having a linear charge density λ is having one of its end at a point P as shown in figure . What is electric field intensity at point Q :
View SolutionTwo long wires having linear charge density λ and −λ are placed parallel to each other at separation ras shown in the figure. The electric field at point P will be
View SolutionTwo infinite line charges with uniform linear charge densities +λ&−λ are kept in such a way that the angle between them is 30∘. The electric field at the symmetric point P at a perpendicular distance r from each line charge is given by:
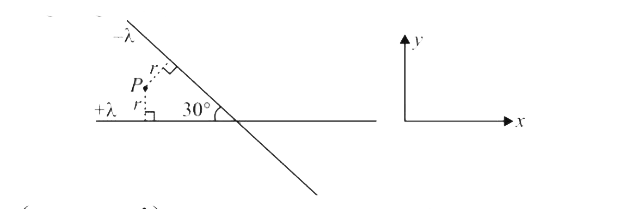
View Solution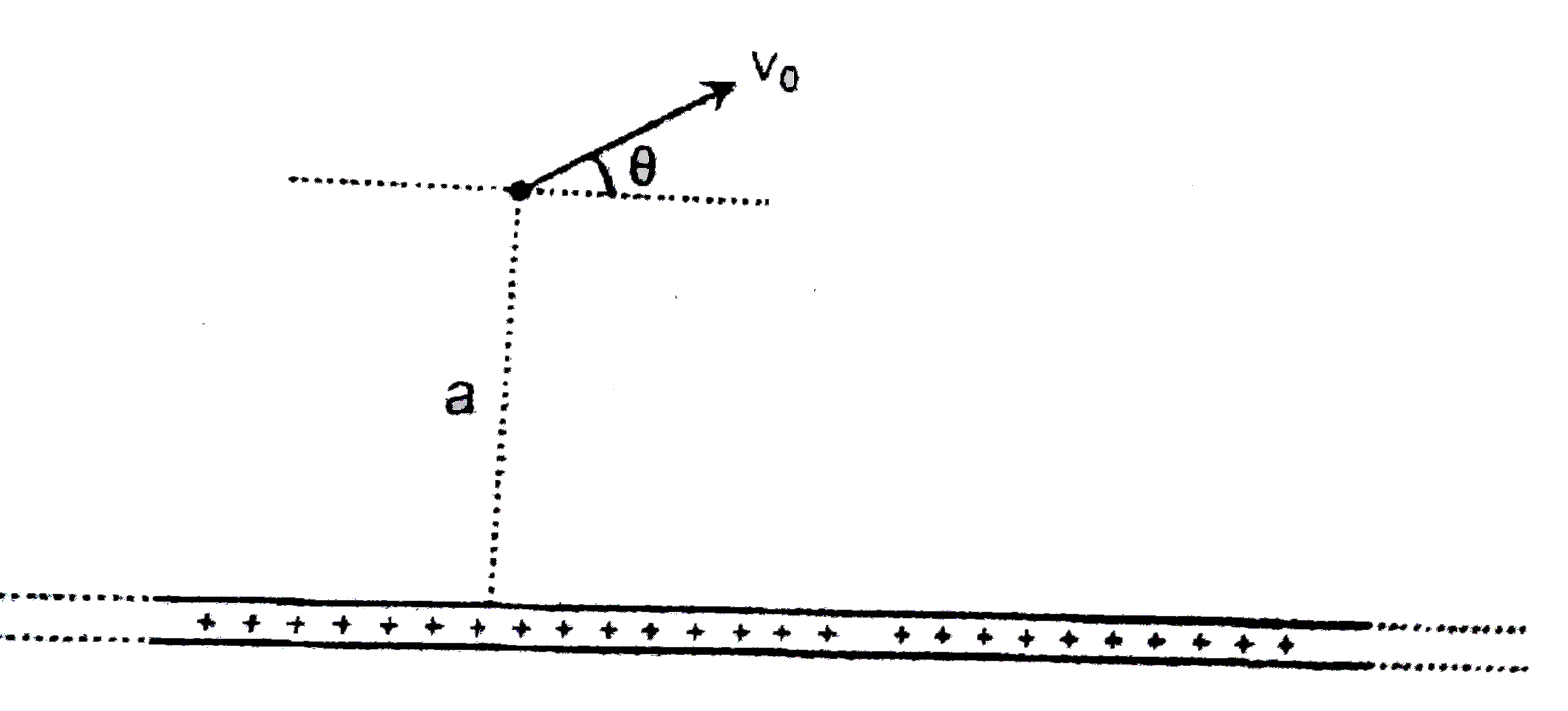
There is an infinite line of uniform linear density of charge +λ. A particle of charge −q & mass m is projected with initial velocity v0 at an angle θ with the line of charge from a distance a from it. The point charge moves in plane containing line charge and point of projection The speed of the particle of found to be minimum when it's distance from the line of charge is ae(nπmε200/qλ). The value of n is (ingnore gravity)
View SolutionAn infinitely long time charge has linear charge density λC/m the line charge is along the line x=0,z=2m find the electric field at point (1,1,1) m.
View Solution
