A block of mass M rests on a smooth horizontal table. There is a small gap in the table under the block through which a pendulum has been attached to the block. The bob of the simple pendulum has mass m and length of the pendulum is L. The pendulum is set into small oscillations in the vertical plane of the figure. Calculate its time period. The table does not interfere with the motion of the string.
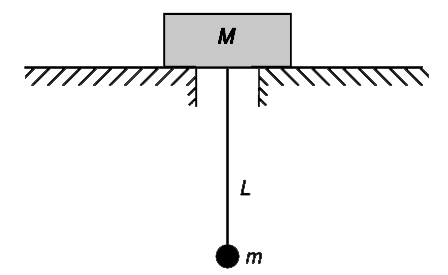
The correct Answer is:T=2π√LMg(M+m)
Step by step video, text & image solution for A block of mass M rests on a smooth horizontal table. There is a small gap in the table under the block through which a pendulum has been attached to the block. The bob of the simple pendulum has mass m and length of the pendulum is L. The pendulum is set into small oscillations in the vertical plane of the figure. Calculate its time period. The table does not interfere with the motion of the string. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ARIHANTCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 3
9 Videos
- SIMPLE HARMONIC MOTIONBOOK - ARIHANTCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 3
9 Videos
- ROTATIONAL MOTIONBOOK - ARIHANTCHAPTER - ROTATIONAL MOTIONEXERCISE - PHYSICS
159 Videos
- SURFACE TENSIONBOOK - ARIHANTCHAPTER - SURFACE TENSIONEXERCISE - Surface tension
33 Videos
Similar Questions
Two particles of mass m1 and m2 are connected by a spring of natural length L and force constant k. The masses are brought close enough so as to compress the spring completely and a string is used to tie the system. Assume that length of spring in this position is close to zero. The system is projected with a velocity V0 along the positive x direction. At the instant it reaches origin at time t = 0, the string snaps and the spring starts opening.
(a) Show that the mass m1(orm2) will are perform SHM in the reference frame attached to the centre of mass of the system. Find the time period of oscillation.
(b) Write the amplitude of m1 and m2 as a function of time. lt( c) Write the X co ordinates of m1 and m2 as a function of time

View SolutionTwo particles of mass m1 and m2 are connected by a spring of natural length L and force constant k. The masses are brought close enough so as to compress the spring completely and a string is used to tie the system. Assume that length of spring in this position is close to zero. The system is projected with a velocity V0 along the positive x direction. At the instant it reaches origin at time t = 0, the string snaps and the spring starts opening.
(a) Show that the mass m1(orm2) will are perform SHM in the reference frame attached to the centre of mass of the system. Find the time period of oscillation.
(b) Write the amplitude of m1 and m2 as a function of time. lt( c) Write the X co ordinates of m1 and m2 as a function of time

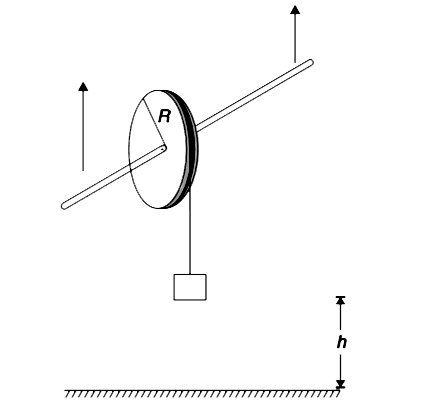
View SolutionThe pulley of radius R can rotate freely about its axle as shown in the figure. A thread is tightly wrapped around the pulley and its free end carries a block of mass m. When the block is at a height h above the ground the system is released (i.e., the pulley is made free to rotate & the block is allowed to fall) and at the same instant the axle is moved up keeping it horizontal all the time. When the block hits the floor the axle has gone up by a distance 2h. Find the angle by which the pulley must have rotated by this time.
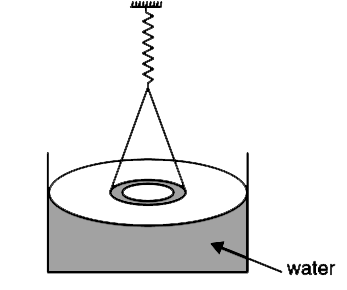
View SolutionA circular ring has inner and outer radii equal to 10mmand30mm respectively Mass of the ring is m=0.7 g. It gently pulled out vertically from a water surface by a sensitive spring. When the spring is stretched 3.4cm from its equilibrium position the ring is on verge of being pulled out from the water surface. If spring constant is k=0.7Nm–1 find the surface tension of water.
View SolutionThe string of a simple pendulum replaced by a uniform rod of length L and mass M while the bob has a mass m . It is allowed to make small oscillation. Its time period is
View SolutionA disc of radius R and mass M is pivoted at the rim and it set for small oscillations. If simple pendulum has to have the same period as that of the disc, the length of the simple pendulum should be
View SolutionA pendulum has a bob of mass m carrying a positive charge q. Length of the pendulum string is L. Beneath the pendulum there is a large horizontal dielectric sheet of charge having uniform surface charge density of sigma C//m^2 . [figure (i)] (a) Find the time period of small oscillations for the pendulum (b) Now the dielectric sheet of charge is tilted so as to make an angle beta with horizontal. Find the angle (a) that the thread makes with vertical in equilibrium position. Find time period of small oscillations in this case. [figure (ii)]
View SolutionThe bob of a simple pendulum (mass m and length l ) dropped from a horizontal position strikes a block of the same mass elastically placed on a horizontal frictionless table. The K.E. of the block will be
View SolutionA simple pendulum has time period T. Charges are now fixed at the point of suspension of the pendulum and on the bob. If the pendulum continues to oscillate, its time period will now be
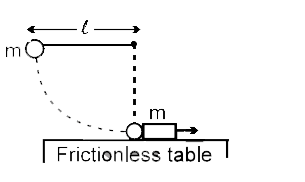
View SolutionThe bob of a simple pendulum of length l dropped from a horizontal position strikes a block of the same mass, placed on a horizontal table (frictionless) as shown in the diagram, the block shall have kinetic energy-
View SolutionHow does period of oscillation of a pendulum depend on mass of the bob and length of the pendulum ?
View Solution(A) : Simple pendulum is said to be executing linear SHM if its angular amplitude is small
(R) : Time period of simple pendulum depends on mass of the pendulum bob.
View SolutionA disc of radius R and mass M is pivoted at the rim and is set for small oscillations. If simple pendulum has to have the same period as that of the disc, the length of the simple pendulum should be
View SolutionThe bob of a simple pendulum (mass m and length l ) dropped from a horizontal position strikes a block of the same mass elastically placed on a horizontal frictionless table. The K.E. of the block will be
View SolutionA disc of radius R and mass M is pivoted at the rim and it set for small oscillations. If simple pendulum has to have the same period as that of the disc, the length of the simple pendulum should be
View Solution
