A block of mass M is placed on top of a hole in a horizontal table. A spring of force constant k is connected to the block through the hole. The other end of the massless spring has a particle of mass m connected to it. With what maximum amplitude can the particle oscillate up and down such that the block does not lose contact with the table?
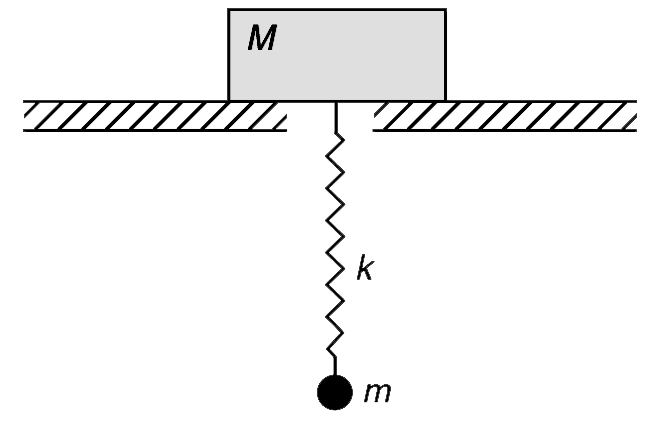
The correct Answer is:Mgk+mgk
Step by step video, text & image solution for A block of mass M is placed on top of a hole in a horizontal table. A spring of force constant k is connected to the block through the hole. The other end of the massless spring has a particle of mass m connected to it. With what maximum amplitude can the particle oscillate up and down such that the block does not lose contact with the table? by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Related Playlists
- BOOK - ARIHANTCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 233videos
SIMPLE HARMONIC MOTION
- BOOK - ARIHANTCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 39videos
SIMPLE HARMONIC MOTION
- BOOK - ARIHANTCHAPTER - ROTATIONAL MOTIONEXERCISE - PHYSICS159videos
ROTATIONAL MOTION
- BOOK - ARIHANTCHAPTER - SURFACE TENSIONEXERCISE - Surface tension33videos
SURFACE TENSION
Similar Practice Problems
- Question 1 - Select One
A block of mass m is connected to two indentical springs of spring constant k which are in turn connected to fixed supports as shown in the figure. Find the time period for small oscillations of the block.
 A2π√mkB2π√m2kC2π√2mkDπ√m2k
A2π√mkB2π√m2kC2π√2mkDπ√m2k - Question 1 - Select One
A block of mass m1 rests on a horizontal table. A string tied to the block is passed on a frictionless pulley fixed at the end of the table and to the other end of string is hung another block of mass m2. The acceleration of the system is
Am2gm1+m2Bm1gm1+m2CgDm2gm1 - Question 1 - Select One
A spring of force constant k is cut into two parts whose lengths are in the ratio 1:2. The two parts are now connected in parallel and a block of mass m is suspended at the end of the combined spring. The period of oscillation of block is
A2π√2m9KB2π√m9KC2π√2m5KD2π√m5K
Similar Questions
A block of mass M is kept on a rough horizontal surface and is attached with massless spring of force constant k .The minimum constant force applied on the other end of the spring to lift the block is
View SolutionA block of mass m is placed on a frictionless horizontal table. Consider a spring of spring constant K whose one end is connected to the block and the other end is connected to a fixed support in such a manner that spring remains horizontal. A positive charge q is given to the block. Suddenly an electric field of magnitude E is switched on in horizontal direction that is in the direction away from the fixed support. What will be the maximum possible elongation of the spring after electric field is switched on?
View SolutionA block of mass M is placed on a horizontal smooth table. It is attached to an ideal spring of force constant k as shown. The free end of the spring is pulled at a constant speed u. Find the maximum extension (x0) in the spring during the subsequent motion.
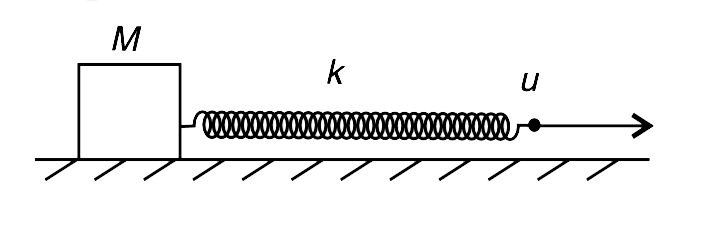 View Solution
View SolutionA block of mass m is connected to another .block of mass M by a massless spring of spring constant k. A constant force f starts action as shown in figure, then:
 View Solution
View SolutionThe block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.
 View Solution
View SolutionA block of mass m =1 kg placed on top of another block of mass M = 5 kg is attached to a horizontal spring of force constant K = 20 N/m as shown in figure. The coefficient of friction between the blocks is µ where as the lower block slides on a frictionless surface. The amplitude of oscillation is 0.4 m. What is the minimum value of µ such that the upper block does not slip over the lower block ?
 View Solution
View SolutionA block A of mass m1 is placed on a horizontal frictionless table. It is connected to one end of a light spring of force constant k whose other end is fixed to a wall. A small block B of mass m2 is placed on block A. The coefficient of static friction between the blocks is μ. The system is displaced slightly from its equilibrium position and released. What is the maximum amplitude of the resulting simple harmonic motion of the system so that the upper block does not slip over the lower block ?
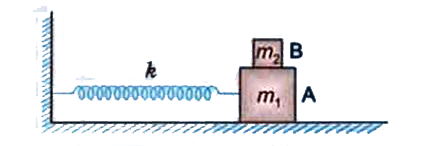 View Solution
View Solution

