A large horizontal turntable is rotating with constant angular speed ω in counterclockwise sense. A person standing at the centre, begins to walk eastward with a constant speed V relative to the table. Taking origin at the centre and X direction to be eastward calculate the maximum X co-ordinate of the person.
The correct Answer is:Vω
Topper's Solved these Questions
Similar Questions
A disc is rotating with constant angular velocity ω in anticlockwise direction. An insect sitting at the centre (which is origin of our co-ordinate system) begins to crawl along a radius at time t=0 with a constant speed V relative to the disc. At time t=0 the velocity of the insect is along the X direction.
(a) Write the position vector (→r) of the insect at time ‘t’.
(b) Write the velocity vector (→v) of the insect at time ‘t’.
(c) Show that the X component of the velocity of the insect become zero when the disc has rotated through an angle θ given by tanθ=1θ.
View SolutionA uniform rod of length l is rotating with constant angular speed ω as shown in figure. Choose the graph which correctly shows the variation of T with x.
_2019_CBT7_E01_017_Q01.png)
View Solution
Knowledge Check
A uniform rod of length l is rotating with constant angular speed ω as shown in figure. Choose the graph which correctly shows the variation of T with x.
_2019_CBT7_E01_017_Q01.png) A
A_2019_CBT7_E01_017_O01.png) B
B_2019_CBT7_E01_017_O02.png) C
C_2019_CBT7_E01_017_O03.png) D
D_2019_CBT7_E01_017_O04.png)
A circular table rotates about a vertical axis with a constant angular speed ω. A circular pan rests on the turn table (with the centre coinciding with centre of table) and rotates with the table. The bottom of the pan is covered with a uniform small thick layer of ice placed at centre of pan. The ice starts melting. The angular speed of the turn table.
Aremains the sameBdecreaseCincreaseDmay increase or decrease dependingon the thickness of ice layer
In the previous problem, initially the insect is at the edge and the disc is rotating with angular speed ω0 in clockwise direction. Now the insect starts walking along the rim with speed v relative to the disc also in clockwise direction. Find new angular speed of platfrom.
View SolutionA circular table rotates about a vertical axis with a constant angular speed ω. A circular pan rests on the turn table (with the centre coinciding with centre of table) and rotates with the table. The bottom of the pan is covered with a uniform small thick layer of ice placed at centre of pan. The ice starts melting. The angular speed of the turn table.
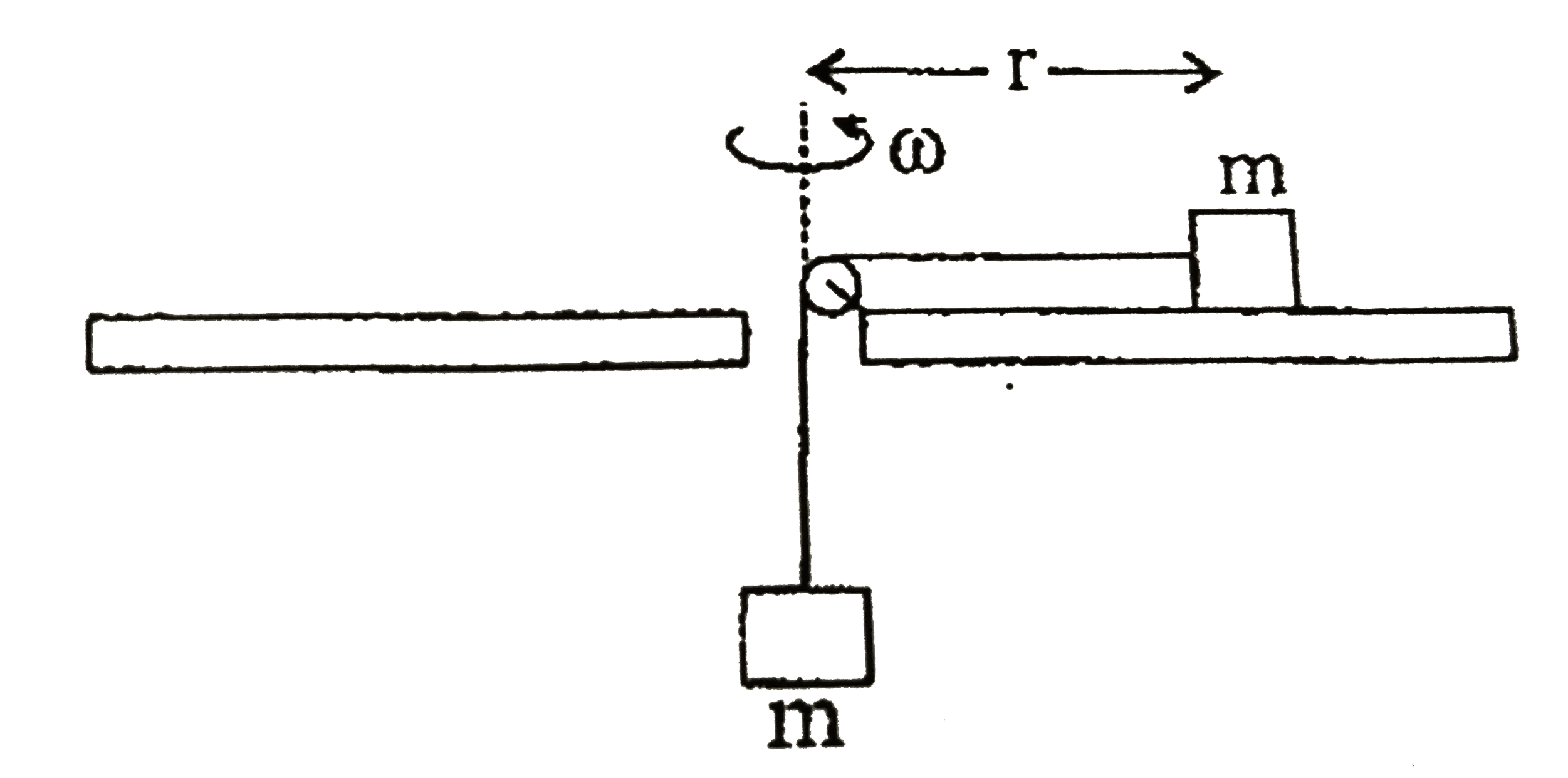
View SolutionTwo equal masses m are attached by a string. One mass lies at radial distance r from the centre of a horizontal turntable which rotates with constant angular velocity ω=2 rad s(1), while the second hangs from the string inside the tumtable's hollow spindle (see fig.) The coefficient of static friction between the turntable and the mass lying on it is μs=0.5. The maximum and minimum values of radius such that the mass lying on the turntable does not slide are rmax+rmin in meter is
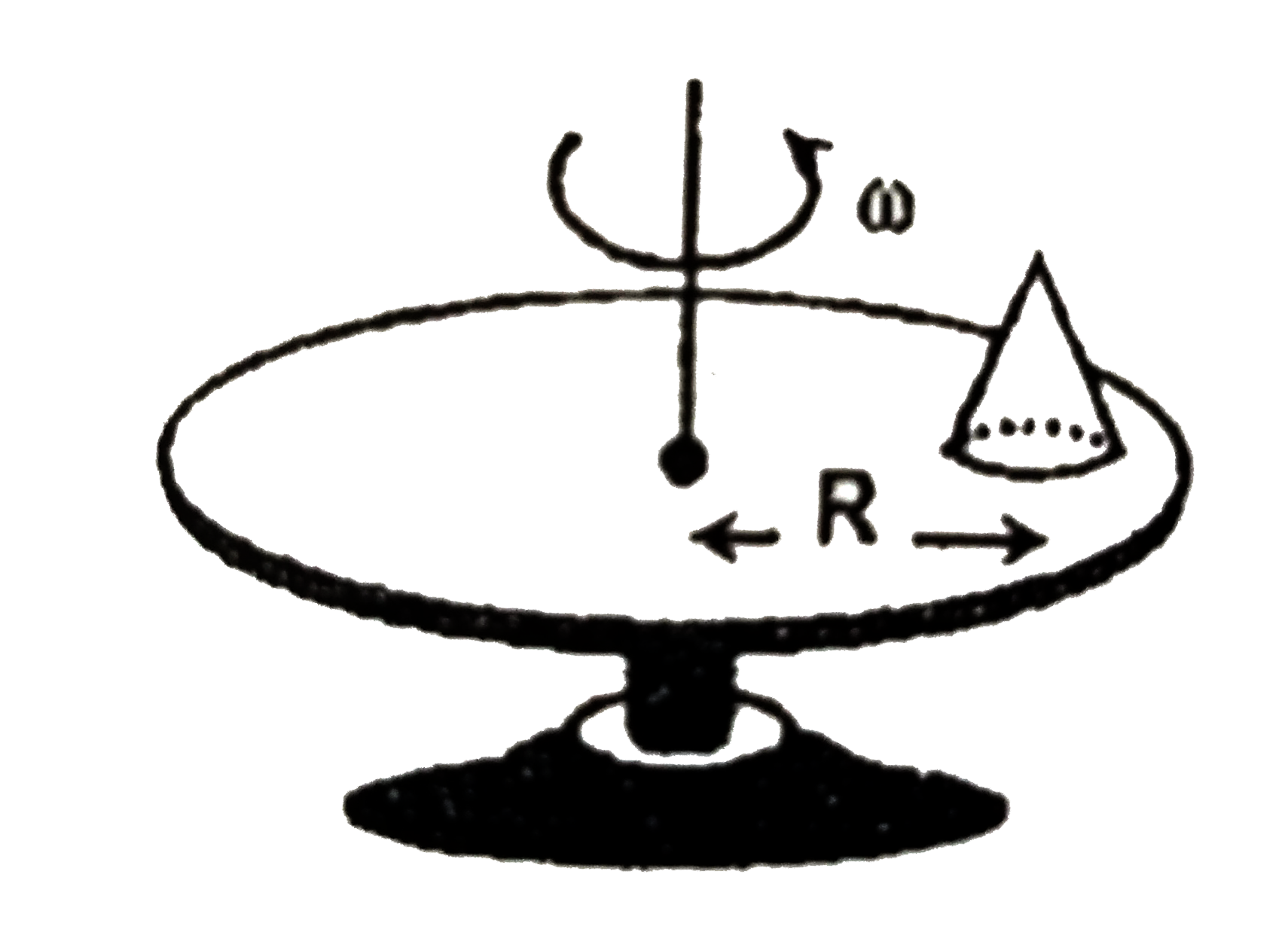
View SolutionA cone of radius r and height h is kept on a turntable rotating with an angular velocity. The friction between te table and the cone is sufficient so that the cone does not slide. The distance between the axis of the cone and the axis of turntable is R(R>>r). the maximum value of ω for which the cone does not topple is √xgrRh, calculate x.
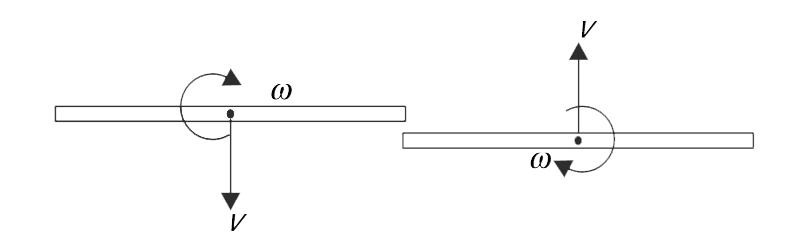
View SolutionTwo identical thin rods are moving on a smooth table, as shown. Both of them are rotating with angular speed ω, in clockwise sense about their centres. Their centres have velocity V in opposite directions. The rods collide at their edge and stick together. Length of each rod is L.
(a) For what value of VωL there will be no motion after collision ?
(b) If the ratio VωL is half the value found in (a) above, what fraction of kinetic energy is lost in the collision?
View SolutionA horizontal disc of radius R and mas 20 M is pivoted to rotate freely about a vertical axis through its centre. A small insect A of mass M and another small insect B of mass mM4 are initially at diametrically opposite points on the periphery of the disc. The whole system is imparted an angular speed ω0 Insect A walks along the diameter with constant velocity v relative to the disc unit it reaches B which remains at rest on the disc. A then eats B and returns to its starting point along the original path with same speed v relative to the disc.
(a) Find the angular speed of the disc when A reaches the centre after eating B.
(b) Plot approximately, the variation of angular speed of the disc with time for the entire journey of the insect A.
View Solution

