A particle of mass m is suspended with the help of a spring and an inextensible string as shown in the figure. Force constant of the spring is k. The particle is pulled down from its equilibrium position by a distance x and released.
(a) Find maximum value of x for which the motion of the particle will remain simple harmonic.
(b) Find maximum tension in the string if
x=mg2k
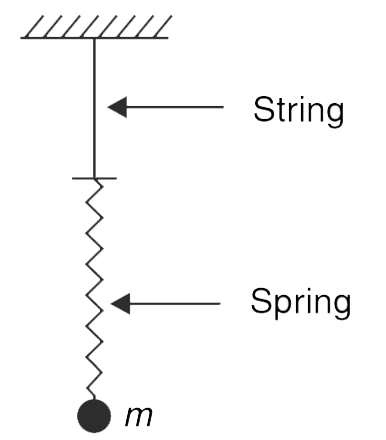
The correct Answer is:(a) mgk,(b)32mg
Step by step video, text & image solution for A particle of mass m is suspended with the help of a spring and an inextensible string as shown in the figure. Force constant of the spring is k. The particle is pulled down from its equilibrium position by a distance x and released. (a) Find maximum value of x for which the motion of the particle will remain simple harmonic. (b) Find maximum tension in the string if x=(mg)/(2k) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:ARIHANTChapter:SIMPLE HARMONIC MOTIONExercise:Level 2
Explore 33 Videos
- SIMPLE HARMONIC MOTIONBook:ARIHANTChapter:SIMPLE HARMONIC MOTIONExercise:Level 3
Explore 9 Videos
- ROTATIONAL MOTIONBook:ARIHANTChapter:ROTATIONAL MOTIONExercise:PHYSICS
Explore 159 Videos
- SURFACE TENSIONBook:ARIHANTChapter:SURFACE TENSIONExercise:Surface tension
Explore 33 Videos
Similar Questions
The block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

View SolutionA particle of mass m is attached with three springs A,B and C of equal force constancts k as shown in figure. The particle is pushed slightly against the spring C and released. Find the time period of oscillation.
 .
.
View Solution
Knowledge Check
A particle of mass m is doing horizontal circular motion with the help of a string (conical pendulu) as shown in the figure. If speed of the particle is constant then,
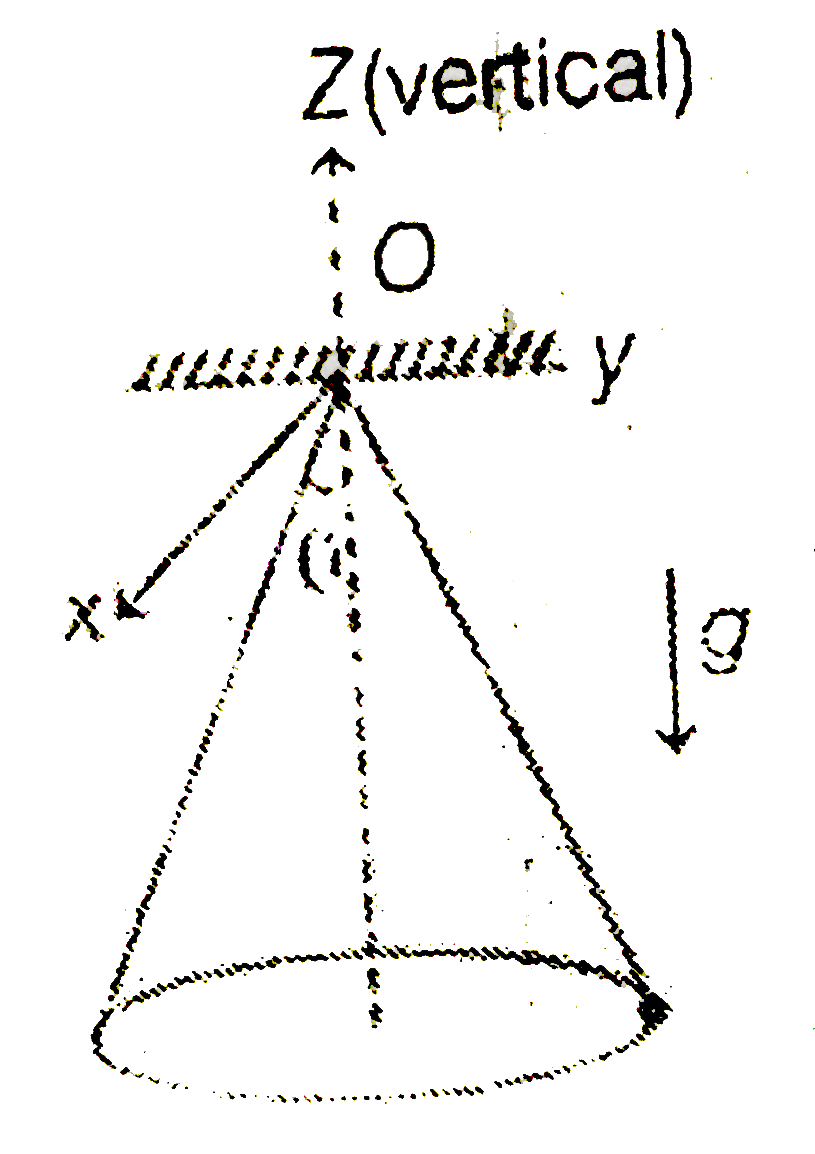 Athe angular momentum of the particle about O is changingBmagnitude of angular momentum about O remains constantCz component of the angular momentum remains conservedDz component of torque is always zero.
Athe angular momentum of the particle about O is changingBmagnitude of angular momentum about O remains constantCz component of the angular momentum remains conservedDz component of torque is always zero.A particle of mass m is attached to three identical springs of spring constant k as shwon in figure. The time period of vertical oscillation of the particle is
 A2π√mkB2π√m2kC2π√m3kDπ√mk
A2π√mkB2π√m2kC2π√m3kDπ√mkIn the figure shown the spring constant is K the mass of the upper disc is m and that of the lower disc is 3m the upper block is depressed down from its equilibrium position by a distance δ=5mg/k and released at t=0 find the velocity of m when normal reaction on 3m is mg
 AzeroBg[m/k]1/2C2g[m/k]1/2D4g[m/k]1/2
AzeroBg[m/k]1/2C2g[m/k]1/2D4g[m/k]1/2
Two identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in figure. When the mass is displaced from equilibrium position by a distance x towards right, find the restoring force.

View SolutionA particle of mass m is asttached to three springs A,B and C of equla force constants k as shown in figure. If the particle is pushed slightly against the spring C and released, find the time period of oscillastion.
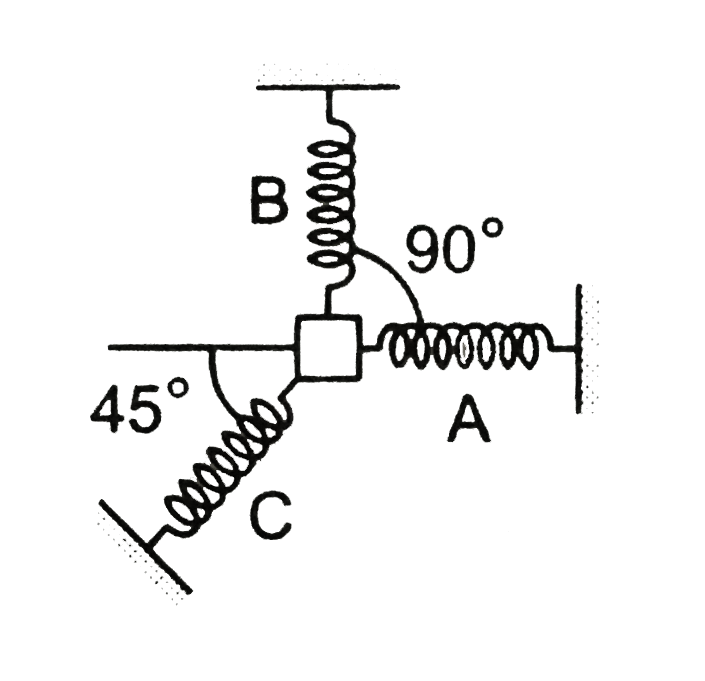
View SolutionA particle of mass m is attached to three identical massless springs of spring constant k as shown in the m 135 figure. The time period of vertical oscillation of the particle is

View SolutionForce constant of a weightless spring is 16Nm−1. A body if mass 1 kg suspended from it is pulled down through 5 cm from its mean position and then released. The maximum kinetic energy of the body will be
View SolutionThe frequency f of vibrations of a mass m suspended from a spring of spring constant k is given by f=Cmxky , where C is a dimensionnless constant. The values of xandy are, respectively,
View Solution