Path traced by a moving particle in space is called trajectory of the particle. Shape of trajectiry is decided by the forces acting on the particle. When a coordinate system is associated with a particle motion, the curve equation in which the particle moves [y=f(x)] is called equation of trajectory. It is just giving us the relation among x and y coordinates of the particle i.e. the locus of particle. To find equation of trajectory of a particle, find first x and y coordinates of the particle as a function of time eliminate the time factor.
In above the velocity (i.e.d→rdt) at t=0 is :-
2bˆj
aˆi
(a−2b)ˆi
None of these
The correct Answer is:B
d→rdt=aˆi−2btˆj at t=0,d→rdt=aˆi
Topper's Solved these Questions
- MISCELLANEOUSBook:ALLENChapter:MISCELLANEOUSExercise:Comprehension 4
Explore 6 Videos
- MISCELLANEOUSBook:ALLENChapter:MISCELLANEOUSExercise:DATA SUFFICIENCY QUESTIONS
Explore 3 Videos
- MISCELLANEOUSBook:ALLENChapter:MISCELLANEOUSExercise:Comprehension 2
Explore 8 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Book:ALLENChapter:KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Exercise:BEGINNER S BOX-7
Explore 8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT Book:ALLENChapter:PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT Exercise:EXERCISE-IV
Explore 8 Videos
Similar Questions
Knowledge Check
Path traced by a moving particle in space is called trajectory of the particle. Shape of trajectiry is decided by the forces acting on the particle. When a coordinate system is associated with a particle motion, the curve equation in which the particle moves [y=f(x)] is called equation of trajectory. It is just giving us the relation among x and y coordinates of the particle i.e. the locus of particle. To find equation of trajectory of a particle, find first x and y coordinates of the particle as a function of time eliminate the time factor.
In above question initial acceleration (i.e.d2→rdt2) of particle is :-A2bˆjBaˆiC−2bˆjDNone of thesePath traced by a moving particle in space is called trajectory of the particle. Shape of trajectiry is decided by the forces acting on the particle. When a coordinate system is associated with a particle motion, the curve equation in which the particle moves [y=f(x)] is called equation of trajectory. It is just giving us the relation among x and y coordinates of the particle i.e. the locus of particle. To find equation of trajectory of a particle, find first x and y coordinates of the particle as a function of time eliminate the time factor.
The position vector of car w.r.t. its starting point is given as →r=atˆi−bt2ˆj where a and b are positive constants. The locus of a particle is:-Aa2y+bx2=0Ba2y=bx2Cy=ba2Day2=b2xIf equation of displacement of a particle y=Asinπt+Bcosπt then motion of particle is
ASimple harmonic motionBLinear motionCUniform circular motionDUniform elliptical motion
A particle moves along the curve y=x2+2x. At what point(s) on the curve are the x and y coordinates of the particle changing at the same rate?
View SolutionThe coordinates of a particle moving in x-y plane at any time t are (2t,t2). Find (a) the trajectory of the particle, (b) velocity of particle at time t and (c) acceleration of particle at any time t.
View SolutionFind the equation of trajectory for the particle moving in circular path as shown.
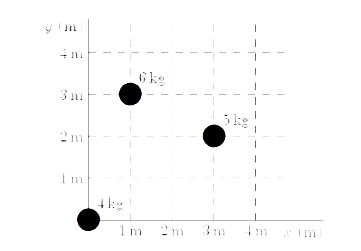
View SolutionThe x and y coordinates of the center of mass of the three-particle system shown below are :
View SolutionThe momentum of a moving particle given by p=tlnt. Net force acting on this particle is defined by equation F=dpdt. The net force acting on the particle is zero at time
View Solution

