Find the equation of trajectory for the particle moving in circular path as shown.
Video Solution
Text Solution
x=rcosθ y=rsinθ x2+y2=r2⇒x2+y2=1
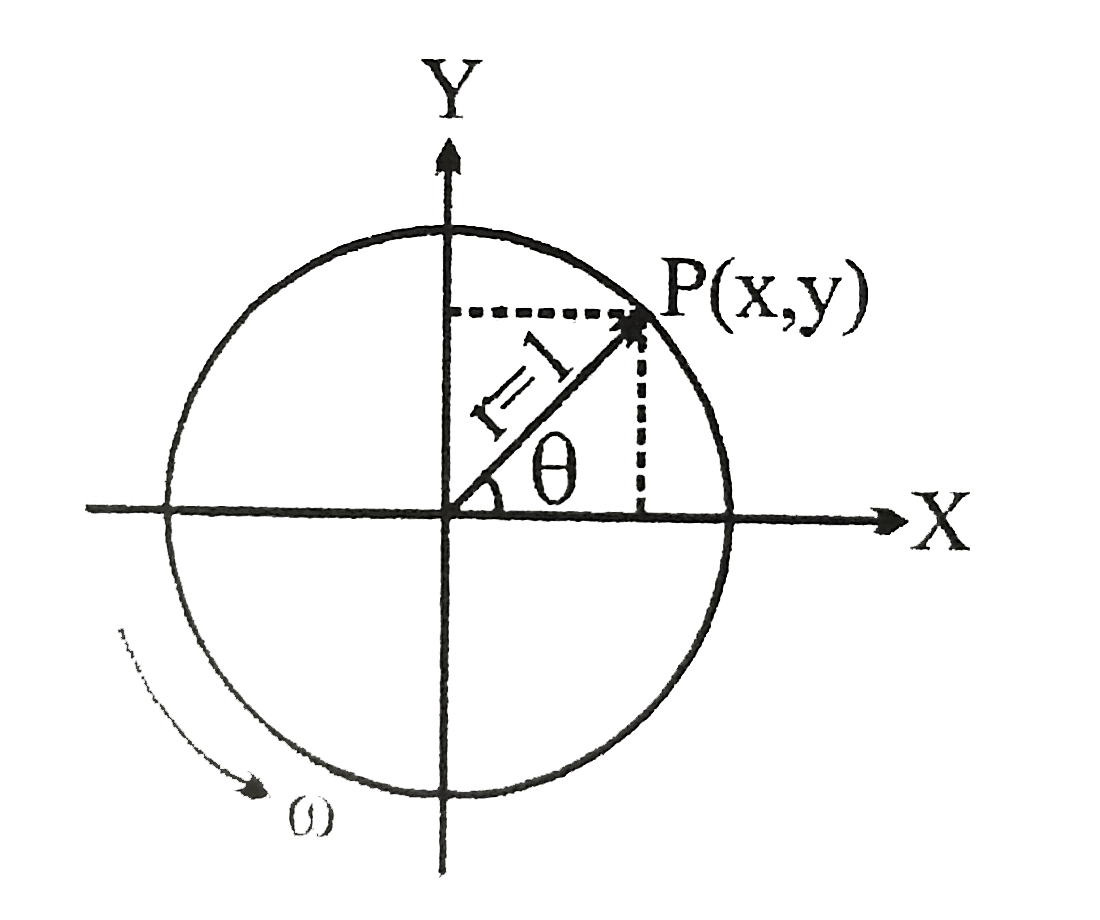
|
Topper's Solved these Questions
- UNIT DIMENSION, VECTOR & BASIC MATHSBOOK - BANSALCHAPTER - UNIT DIMENSION, VECTOR & BASIC MATHSEXERCISE - Solved Example
17 Videos
- UNIT DIMENSION, VECTOR & BASIC MATHSBOOK - BANSALCHAPTER - UNIT DIMENSION, VECTOR & BASIC MATHSEXERCISE - PRACTICE EXERCISE
4 Videos
- KINETIC THEORY OF GASESBOOK - BANSALCHAPTER - KINETIC THEORY OF GASESEXERCISE - Section-B
13 Videos
Similar Questions
Knowledge Check
Statement-I : When the direction of motion of a particle moving in a circular path is reversed the direction of radial acceleration still remains the same (at the given point).
Statement-II : Particle revolves on circular path in any direction such as clockwise or anticlockwise the direction of radius accelerationis always towards the centre of the circular path.Aaba+btm/sBaba−btm/sC2aba+btm/sD2aba−btm/sPath traced by a moving particle in space is called trajectory of the particle. Shape of trajectiry is decided by the forces acting on the particle. When a coordinate system is associated with a particle motion, the curve equation in which the particle moves [y=f(x)] is called equation of trajectory. It is just giving us the relation among x and y coordinates of the particle i.e. the locus of particle. To find equation of trajectory of a particle, find first x and y coordinates of the particle as a function of time eliminate the time factor.
The position vector of car w.r.t. its starting point is given as →r=atˆi−bt2ˆj where a and b are positive constants. The locus of a particle is:-Aa2y+bx2=0Ba2y=bx2Cy=ba2Day2=b2xIt mass, speed and radius of the circle of a particle moving uniformly in a circular path are all increased by 50% , the necessary force required to maintain the body moving in the circular path will have to be increased by
A225%B125%C150%D100%
A ball is released from height h as shown in fig. Find the condition for the particle to complete the circular path.
View SolutionThe angular velocity of a particle moving in a circle realative to the center of the circle is equal to ω. Find the angular velocity of the particle relative to a point on the circular path.
View SolutionIf the speed of a given charged particle moving on a circular path in a given magnetic field is doubled then the particle starts moving on a circular path of double radius.
View SolutionThe ratio of periods of α-particle and proton moving on circular path in uniform magnetic field is _______.
View SolutionThe angular acceleration of a particle moving along a circular path with uniform speed is
View Solution
